Nonnegative derivative that is not identically zero on any interval implies increasing
Statement
On an open interval
Suppose is a function on an open interval that may be infinite in one or both directions (i..e, is of the form , , , or ). Suppose the derivative of exists and is nonnegative everywhere on , i.e., for all . Further, suppose that there is no sub-interval of such that for all in the sub-interval. Then, is an increasing function on , i.e.:
On a general interval
Suppose is a function on an interval that may be infinite in one or both directions and may be open or closed at either end. Suppose is a continuous function on all of and that the derivative of exists and is nonnegative everywhere on the interior of , i.e., for all other than the endpoints of (if they exist). Further, suppose that there is no sub-interval of such that for all in the sub-interval. Then, is an increasing function on , i.e.:
Isolated points version
Formulation and relationship between the formulations
The following is true:
The derivative is zero only at isolated points, i.e., the set of points at which the derivative is zero is a discrete subset of the reals The derivative is not zero on any interval
Thus, the condition of derivative not being zero on any interval can be replaced by the stronger condition that the derivative is zero only at isolated points. The resulting statement is somewhat weaker (i.e., less powerful) because it assumes a stronger hypothesis on the function. In other words, there do exist functions that satisfy the hypothesis with the not zero on any interval version and are hence increasing but where the set of points for the derivative to be zero is not a discrete subset. (See example below).
For most practical purposes, the isolated points formulation suffices.
Example
Typical example: point of inflection with horizontal tangent
These are examples where a critical point (point of derivative being zero) coincides with a point of inflection (point where second derivative changes sign). To the left of the critical point, the derivative is positive and decreasing. At the critical point, the derivative becomes zero, attaining its local minimum. To the right of the critical point, the derivative is positive and decreasing. Thus, the function itself is increasing on the left of the critical point and increasing on the right of the critical point. Although the derivative drops to zero at the critical point, the function does not actually stop increasing.
| Function | General expression for derivative | Why the derivative is always nonnegative | Points where the derivative is zero | Graph of function (blue) with derivative (purple) |
|---|---|---|---|---|
| cube function on all of | it's a positive constant times a square | at only. | 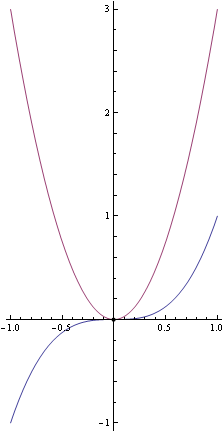
| |
| on all of | We use that for all | at integer multiples of only. This forms a discrete set, i.e., they are all isolated points. | Fill this in later |
Example to illustrate the distinction with the isolated points version
Consider the function:
is a continuous function, and we can hence define:
Thus, by the fundamental theorem of calculus, . Note that by definition, for all , because the outer part of the composite is an absolute value function. Also, the set of points where is , which is not a discrete set (in particular, the point 0 is not an isolated point and is in fact a limit point). However, it is true that the zero set of does not contain any intervals, and hence we can still conclude that is an increasing function on all of .
Related facts
Similar facts
- Positive derivative implies increasing
- Zero derivative implies locally constant
- Negative derivative implies decreasing