Cube function
This article is about a particular function from a subset of the real numbers to the real numbers. Information about the function, including its domain, range, and key data relating to graphing, differentiation, and integration, is presented in the article.
View a complete list of particular functions on this wiki
Definition
This function, termed the cube function or cubing function or cube map, is the function that sends any element to its cube, i.e., to its third power. It is defined as:
Key data
| Item | Value |
|---|---|
| default domain | all real numbers, i.e., all of |
| range | all real numbers |
| period | not a periodic function |
| inverse function | cube root function (both the cube function and the cube root function are one-one functions) |
| first derivative | , i.e., thrice the square function |
| second derivative | , i.e., six times the identity function |
| antiderivative | , i.e., times the fourth power function |
| important symmetries | the origin is a point of half turn symmetry |
| local minimum values and points of attainment | there are no local minimum values because the function is increasing throughout its domain |
| local maximum values and points of attainment | there are no local maximum values because the function is increasing throughout its domain |
| points of inflection (both coordinates) | the origin |
| intervals of increase/decrease and concave up/down | increasing and concave down on . increasing and concave up on . |
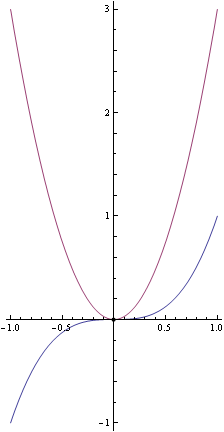
Graph
Below is the graph of the function, with domain restricted to :
Below is the graph of the function and its derivative, with domain restricted to :









![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)