Higher derivative test
This article describes a test that can be used to determine whether a point in the domain of a function gives a point of local, endpoint, or absolute (global) maximum or minimum of the function, and/or to narrow down the possibilities for points where such maxima or minima occur.
View a complete list of such tests
This article describes a variation of second derivative test that is intended to remedy a specific defect, namely second derivative test is inconclusive for function at critical point where second derivative is zero.
Statement
What this test is for
The term higher derivative test or higher derivative tests is used for a slight modification of the second derivative test that is used to determine whether a critical point for a function is a point of local maximum, local minimum, or neither. The higher derivative test can help resolve some of the inconclusive cases of the second derivative test.
What the test says
Suppose is a function and is a point in the interior of the domain of . Suppose is a critical point for of the type where . Suppose further that there exists a natural number such that:
- The derivative of at , namely , exists and is nonzero.
- All lower order derivatives of at , starting onward, are zero. In other words, .
In other words, is the first nonzero-valued derivative of at .
Then, we have the following:
| Case on parity of | Case on sign of | Conclusion about at | Prototypical example (words) | Prototypical example (picture) |
|---|---|---|---|---|
| even | negative | strict local maximum (mimics the second derivative test where ) | (more generally, we can take as for a natural number, and ) | |
| even | positive | strict local minimum (mimics the second derivative test where ) | (more generally, we can take as for a natural number, and ) | |
| odd | negative | neither local maximum nor local minimum. The point is a point of decrease for the function. In fact, it is also a point of inflection, though that is not of relevance here. | (more generally, we can take as for a natural number, and ) | 
|
| odd | positive | neither local maximum nor local minimum. The point is a point of increase for the function. In fact, it is also a point of inflection, though that is not of relevance here. | (more generally, we can take as for a natural number, and ) | 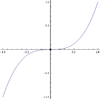
|
Facts used
Proof
The proof essentially follows from Fact (1), which covers a much larger body of cases.
Related tests
- First derivative test
- Second derivative test
- One-sided derivative test
- One-sided version of second derivative test
Strength of the test
Relation with second derivative test
The test contains the second derivative test under the subcase . Further, in case the second derivative test is inconclusive, it is possible that the higher derivative test would still be conclusive. So, we can think of it as a modification of the second derivative test that helps address some of the inadequacies of the second derivative test.
Note that the actual application of the higher derivative test always begins with an attempt to use the second derivative test, so for the cases where the second derivative test is conclusive, the execution of both tests looks exactly the same.
Ease of use
The main advantage of using the higher derivative test is that in cases where it is conclusive, the test is often easier to apply than the first derivative test. This, in turn, is because the test only requires the computation of formal expressions for derivatives and evaluation of the signs of these expressions at a point rather than on an interval. Evaluation at a point often requires less symbolic/algebraic manipulation.
Conclusive and inconclusive cases
Inconclusive cases
| What problem do we run into? | What kind of trouble do we have? | Can we use the first derivative test? |
|---|---|---|
| For critical points that are of the does not exist type, the test cannot be applied. | The test doesn't make sense | We may or may not be able to use the first derivative test. |
| The higher derivatives cease being defined before they get a chance to become nonzero. For instance, if and does not exist, the test is inconclusive. | The test crucially relies on determining the position and sign of the first nonzero derivative. If the higher derivative ceases to exist before it becomes nonzero, the test cannot be used. | We may or may not be able to use the first derivative test. |
| All higher derivatives at the point are zero. | The test crucially relies on determining the position and sign of the first nonzero derivative. If all higher derivatives are zero, we cannot use the test. | We may or may not be able to use the first derivative test. |
Conclusive cases
- Higher derivative test is conclusive for function with algebraic derivative
- Higher derivative test is conclusive for locally analytic function: In particular, it is always conclusive for polynomials, rational functions, and polynomials in and .
























