Sine-squared function

This article is about a particular function from a subset of the real numbers to the real numbers. Information about the function, including its domain, range, and key data relating to graphing, differentiation, and integration, is presented in the article.
View a complete list of particular functions on this wiki

Definition

This function, denoted ${\sin }^2$, is defined as the composite of the square function and the sine function. Explicitly, it is the map:

$x\mapsto (\sin x{)}^2$

For brevity, we write $(\sin x{)}^2$ as ${\sin }^{2}x$.

Key data

Item	Value
Default domain	all real numbers, i.e., all of $\mathbb{R}$
range	$[0,1]$, i.e., $\{y\mid 0\le y\le 1\}$ absolute maximum value: 1, absolute minimum value: 0
period	$\pi$, i.e., $180{}^{\circ }$
local maximum value and points of attainment	All local maximum values are equal to 1, and are attained at odd integer multiples of $\pi /2$.
local minimum value and points of attainment	All local minimum values are equal to 0, and are attained at integer multiples of $\pi$.
points of inflection (both coordinates)	odd multiples of $\pi /4$, with value 1/2 at each point.
derivative	$x\mapsto \sin (2x)=2\sin x\cos x$, i.e., double-angle sine function.
second derivative	$x\mapsto 2\cos (2x)$
$n^{th}$ derivative	$2^{n-1}$ times an expression that is $\pm \sin$ or $\pm \cos$ of $2x$, depending on the remainder of $n$ mod $4$
antiderivative	$x\mapsto \frac{x}{2}-\frac{\sin (2x)}{4}+C$
mean value over a period	1/2
expression as a sinusoidal function plus a constant function	$(1/2)-\cos (2x)/2$
important symmetries	even function (follows from composite of even function with odd function is even, the square function being even, and the sine function being odd) more generally, miror symmetry about any vertical line of the form $x=n\pi /2$, $n$ an integer. Also, half turn symmetry about all points of the form $(n\pi /2+\pi /4,1/2)$.
interval description based on increase/decrease and concave up/down	For each integer $n$, the interval from $n\pi$ to $(n+1)\pi$ is subdivided into four pieces: $(n\pi ,n\pi +\pi /4)$: increasing and concave up $(n\pi +\pi /4,n\pi +\pi /2)$: increasing and concave down $(n\pi +\pi /2,n\pi +3\pi /4)$: decreasing and concave down, $(n\pi +3\pi /4,(n+1)\pi )$: decreasing and concave up
power series and Taylor series	The power series about 0 (which is hence also the Taylor series) is $\sum _{k=1}^{\mathrm{\infty }}\frac{(2{)}^{2k-1}(-1{)}^{k-1}{x}^{2k}}{(2k)!}=x^2-\frac{x^4}{3}+\frac{2x^6}{45}-\dots$ It is a globally convergent power series.

Identities

We have the following important identities involving ${\sin }^2$:

• ${\sin }^{2}x+{\cos }^{2}x=1$, relating it to the cosine-squared function.
• $\cos (2x)=1-2{\sin }^{2}x$, or equivalently, ${\sin }^{2}x=(1-\cos (2x))/2$.

Graph

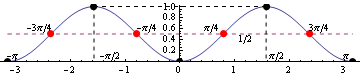
Here is the graph on the interval $[-2\pi ,2\pi ]$, drawn to scale:

Here is a close-up view of the graph between $-\pi$ and $\pi$. The dashed horizontal line indicates the mean value of $1/2$:

The red dotted points indicate the points of inflection and the black dotted points indicate local extreme values.

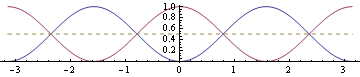
Here is a picture showing the function (blue) and the cosine-squared function (purple) with the dashed line being $y=1/2$. The picture illustrates that ${\sin }^{2}x+{\cos }^{2}x=1$:

Differentiation

First derivative

WHAT WE USE: chain rule for differentiation, differentiation rule for power functions, sine function#First derivative, double angle cosine formula

We have:

$\frac{d}{dx}({\sin }^{2}x)=\sin (2x)$

We can do this two ways.

Using the chain rule for differentiation, we have:

$\frac{d}{dx}[(\sin x{)}^2]=2\sin x\frac{d}{dx}(\sin x)=2\sin x\cos x$

By the double angle sine formula, this is the same as $\sin (2x)$.

Alternatively, using the double angle cosine formula, we rewrite:

${\sin }^{2}x=\frac{1-\cos (2x)}{2}$

Differentating, we get:

$\frac{d}{dx}({\sin }^{2}x)=\frac{-1}{2}\frac{d}{dx}(\cos (2x))=\frac{-1}{2}\cdot 2\cdot (-\sin (2x))=\sin (2x)$

Second derivative

Differentiating the derivative again, we get:

$\frac{d^2}{d{x}^2}({\sin }^{2}x)=\frac{d}{dx}[\sin (2x)]=\frac{d}{d(2x)}[\sin (2x)]\frac{d(2x)}{dx}=2\cos (2x)$

Graph of function with derivative

Fill this in later

Points and intervals of interest

Critical points

Consider $f(x)={\sin }^{2}x$. As computed earlier, we have:

$f^{\prime }(x)=\sin (2x)$

This equals zero precisely at the points $x$ where $2x=n\pi ,n\in \mathbb{Z}$, so $x=n\pi /2,n\in \mathbb{Z}$. In other words, the critical points occur at the integer multiples of $\pi /2$.

Intervals of increase and decrease

The function $f^{\prime }$ is positive for $2x\in (2n\pi ,(2n+1)\pi )$, with $n\in \mathbb{Z}$ and negative for $2x\in ((2n+1)\pi ,(2n+2)\pi )$, with $n\in \mathbb{Z}$. Dividing by 2, we get:

• $f$ is increasing on intervals of the form $(n\pi ,n\pi +\pi /2)$, $n\in \mathbb{Z}$.
• $f$ is decreasing on intervals of the form $(n\pi +\pi /2,n\pi +\pi )$, $n\in \mathbb{Z}$.

Local extreme values

From the information on the intervals of increase and decrease, we conclude that:

• $f$ attains its local maximum values at points of the form $n\pi +\pi /2$, $n\in \mathbb{Z}$, and all the values are equal to 1.
• $f$ attains its local minimum values at points of the form $n\pi$, $n\in \mathbb{Z}$, and all the values are equal to 0.

Intervals of concave up and concave down

The second derivative $f^{″}$ is the function $x\mapsto 2\cos (2x)$. This is positive for $2x\in (2n\pi -\pi /2,2n\pi +\pi /2)$ and negative for $2x\in (2n\pi +\pi /2,2n\pi +3\pi /2)$, where $n\in \mathbb{Z}$. We thus get:

• $f$ is concave up on intervals of the form $(n\pi -\pi /4,n\pi +\pi /4)$, with $n\in \mathbb{Z}$.
• $f$ is concave down on intervals of the form $(n\pi +\pi /4,n\pi +3\pi /4)$, with $n\in \mathbb{Z}$.

Points of inflection

From the determination of intervals where $f$ is concave up and concave down, we discover that the points of inflection are the points with $x$-coordinate an odd multiple of $\pi /4$. The function value at all these points is $1/2$.

• At points with $x=n\pi +\pi /4,n\in \mathbb{Z}$, the function is transitioning from concave up (on the left) to concave down (on the right).
• At points with $x=n\pi +3\pi /4,n\in \mathbb{Z}$, the function is transitioning from concave down (on the left) to concave up (on the right).

Integration

First antiderivative

WHAT WE USE: double angle cosine formula, recursive version of integration by parts, integration of linear transform of function

Using the double angle cosine formula

${\sin }^{2}x=\frac{1-\cos (2x)}{2}$

We can now do the integration:

$\int {\sin }^{2}xdx=\int \frac{1-\cos (2x)}{2}dx=\int \frac{1}{2}dx-\int \frac{\cos (2x)}{2}dx=\frac{x}{2}-\frac{1}{2}\int \cos (2x)dx$

To integrate $\cos (2x)$, we use the method of integration of linear transform of function to get $\sin (2x)/2$. Plugging that in, we get:

$\frac{x}{2}-\frac{1}{2}(\frac{\sin (2x)}{2})+C=\frac{x}{2}-\frac{\sin (2x)}{4}+C$

Using integration by parts

We rewrite ${\sin }^{2}x=(\sin x)(\sin x)$ and use integration by parts in its recursive version:

$\int {\sin }^{2}xdx=(\sin x)(-\cos x)-\int (\cos x)(-\cos x)dx=-\sin x\cos x+\int {\cos }^{2}xdx$

We now rewrite ${\cos }^{2}x=1-{\sin }^{2}x$ and obtain:

$\int {\sin }^{2}xdx=-\sin x\cos x+\int (1-{\sin }^{2}x)dx$

Setting $I$ to be a choice of antiderivative so that the above holds without any freely floating constants, we get:

$I=-\sin x\cos x+x-I$

Rearranging, we get:

$2I=x-\sin x\cos x$

This gives:

$I=\frac{x-\sin x\cos x}{2}$

So the general antiderivative is:

$\frac{x-\sin x\cos x}{2}+C$

Using the double angle sine formula

$\sin (2x)=2\sin x\cos x$

, we can verify that this matches with the preceding answer.

For a given continuous function on a connected set, antiderivatives obtained by different methods must differ by a constant. In some cases, the antiderivatives may be exactly equal, but this is not necessary in general.
See zero derivative implies locally constant

Graph of function with antiderivative

In the picture below, we depict ${\sin }^2$ (blue) and the function $x\mapsto \frac{x}{2}-\frac{\sin (2x)}{4}$ (purple). This is the unique antiderivative that takes the value 0 at 0. The other antiderivatives can be obtained by vertically shifting the purple graph:

The black dots correspond to local extreme values for ${\sin }^2$, and the red dots correspond to points of inflection for the antiderivative. Each black dot is in the same vertical line as a red dot, as we should expect, because points of inflection for the antiderivative correspond to local extreme values for the original function. Further:

• The antiderivative is increasing everywhere because ${\sin }^2$ is everywhere nonnegative, and is zero only at isolated points.
• The antiderivative is concave up on those intervals where ${\sin }^2$ is increasing, i.e., intervals of the form $(n\pi ,n\pi +\pi /2)$ as $n$ varies over the integers.
• The antiderivative is concave down on those intervals where ${\sin }^2$ is decreasing, i.e., intervals of the form $(n\pi +\pi /2,n\pi +\pi )$ as $n$ varies over the integers.

Definite integrals

The $x/2$ part in the antiderivative signifies that the linear part of the antiderivative of ${\sin }^2$ has slope $1/2$, and this is related to the fact that ${\sin }^2$ has a mean value of $1/2$ on any interval of length equal to the period. It is in fact clear that the function is a sinusoidal function about $x=1/2$.

Thus, we have:

$\underset{a}{\overset{a+n\pi }{\int }}{\sin }^{2}xdx=\frac{n\pi }{2}$

where $n$ is an integer.

The mean value of ${\sin }^2$ over an interval of length equal to a multiple of the period is $1/2$. Thus, for very large intervals, the mean value of ${\sin }^2$ is very close to 1/2, even though it need not be exactly 1/2. Specifically:

$\underset{x\to \mathrm{\infty }}{lim}\frac{1}{x}\underset{a}{\overset{a+x}{\int }}{\sin }^{2}tdt=\frac{1}{2}$

Transformed versions

Based on the integration of ${\sin }^2$, we can also integrate the square of any sinusoidal function using the integration of linear transform of function:

$\int {\sin }^2(mx+\phi )dx=\frac{x}{2}-\frac{\sin (2(mx+\phi ))}{4m}+C$

We thus see that the mean value of this function is also $1/2$ over any interval of length a multiple of the period $\pi /m$. Also, over a sufficiently long interval, the mean value is close to 1/2:

$\underset{x\to \mathrm{\infty }}{lim}\frac{1}{x}\underset{a}{\overset{a+x}{\int }}{\sin }^2(mt+\phi )dt=\frac{1}{2}$

Higher antiderivatives

It is possible to antidifferentiate ${\sin }^2$ more than once. The $n^{th}$ antiderivative is the sum of a polynomial of degree $n$ and a trigonometric function with a period of $\pi$.

Power series and Taylor series

Computation of power series

We can use the identity:

${\sin }^{2}x=\frac{1-\cos (2x)}{2}$

along with the power series for the cosine function, to find the power series for ${\sin }^2$.

The power series for the cosine function converges to the function everywhere, and is:

$\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\dots =\sum _{k=0}^{\mathrm{\infty }}\frac{(-1{)}^k{x}^{2k}}{(2k)!}$

The power series for $\cos (2x)$ is:

$\cos (2x)=1-\frac{(2x{)}^2}{2!}+\frac{(2x{)}^4}{4!}-\frac{(2x{)}^6}{6!}+\dots =\sum _{k=0}^{\mathrm{\infty }}\frac{(-1{)}^k{2}^{2k}{x}^{2k}}{(2k)!}$

The power series for $1-\cos (2x)$ is:

$1-\cos (2x)=\frac{(2x{)}^2}{2!}-\frac{(2x{)}^4}{4!}+\frac{(2x{)}^6}{6!}-\dots =\sum _{k=1}^{\mathrm{\infty }}\frac{(-1{)}^{k-1}{2}^{2k}{x}^{2k}}{(2k)!}$

Dividing by 2, we get the power series for ${\sin }^{2}x$:

${\sin }^{2}x=\frac{2^1{x}^2}{2!}-\frac{2^3{x}^4}{4!}+\frac{2^5{x}^6}{6!}-\dots =\sum _{k=1}^{\mathrm{\infty }}\frac{(-1{)}^{k-1}{2}^{2k-1}{x}^{2k}}{(2k)!}$

Here's another formulation with the first few terms written more explicitly:

${\sin }^{2}x=x^2-\frac{x^4}{3}+\frac{2x^6}{45}-\dots$

Taylor polynomials as approximations

Note that since ${\sin }^2$ is an even function, all its Taylor polynomials are also even polynomials. In the figure below, we consider the graphs of ${\sin }^2$ and its second, fourth, and sixth Taylor approximations.

• Second Taylor polynomial $P_2(x)$, which equals the third Taylor polynomial, $P_3(x)$, is $x^2$.
• Fourth Taylor polynomial $P_4(x)$, which equals the fifth Taylor polynomial, $P_5(x)$, is $x^2-\frac{x^4}{3}$.
• Sixth Taylor polynomial, $P_6(x)$, which equals the seventh Taylor polynomial $P_7(x)$, is $x^2-\frac{x^4}{3}+\frac{2x^6}{45}$.

Limit computations

Order of zero

We get the following limit from the power series:

$\underset{x\to 0}{lim}\frac{{\sin }^{2}x}{x^2}=1$

Thus, the order of the zero of ${\sin }^2$ at zero is 2 and the residue is 1.

This limit can be computed in many ways:

Name of method for computing the limit	Details
Simple manipulation, using $\underset{x\to 0}{lim}(\sin x)/x=1$	$\underset{x\to 0}{lim}\frac{{\sin }^{2}x}{x^2}=\underset{x\to 0}{lim}{(\frac{\sin x}{x})}^2={(\underset{x\to 0}{lim}\frac{\sin x}{x})}^2=1^2=1$
Using the L'Hopital rule	$\underset{x\to 0}{lim}\frac{{\sin }^{2}x}{x^2}\stackrel{*}{=}\underset{x\to 0}{lim}\frac{\sin (2x)}{2x}\stackrel{*}{=}\underset{x\to 0}{lim}\frac{2\cos (2x)}{2}=1$
Using the power series	We have ${\sin }^{2}x=x^2-\frac{x^4}{3}+\dots$, so we get $\frac{{\sin }^{2}x}{x^2}=1-\frac{x^2}{3}+\dots$. Taking the limit as $x\to 0$ gives 1.

Higher order limits

We have the limit:

$\underset{x\to 0}{lim}\frac{x^2-{\sin }^{2}x}{x^4}=\frac{1}{3}$

This limit can be computed in many ways:

Name of method for computing the limit	Details
Using $\underset{x\to 0}{lim}\frac{x-\sin x}{x^3}=1/6$ and $\underset{x\to 0}{lim}\frac{\sin x}{x}=1$	We have $\underset{x\to 0}{lim}\frac{x^2-{\sin }^{2}x}{x^4}=\underset{x\to 0}{lim}\frac{x-\sin x}{x^3}\cdot \frac{x+\sin x}{x}=\underset{x\to 0}{lim}\frac{x-\sin x}{x^3}\cdot \underset{x\to 0}{lim}\frac{x+\sin x}{x}$. The first limit is $1/6$ and the second limit is 2 from the given data. We thus get $(1/6)\cdot 2=1/3$.
Using the L'Hopital rule	$\underset{x\to 0}{lim}\frac{x^2-{\sin }^{2}x}{x^4}\stackrel{*}{=}\underset{x\to 0}{lim}\frac{2x-\sin (2x)}{4x^3}\stackrel{*}{=}\underset{x\to 0}{lim}\frac{2-2\cos (2x)}{12x^2}\stackrel{*}{=}\underset{x\to 0}{lim}\frac{4\sin (2x)}{24x}\stackrel{*}{=}\underset{x\to 0}{lim}\frac{8\cos (2x)}{24}=1/3$.
Using the power series	We have ${\sin }^{2}x=x^2-\frac{x^4}{3}+O(x^6)$, so $\frac{x^2-{\sin }^{2}x}{x^4}=\frac{1}{3}-O(x^2)$, so the limit as $x\to 0$ is 1/3.