Limit: Difference between revisions

Revision as of 20:15, 22 December 2012

ORIGINAL FULL PAGE: Limit
STUDY THE TOPIC AT MULTIPLE LEVELS:
ALSO CHECK OUT: Quiz (multiple choice questions to test your understanding) |Page with videos on the topic, both embedded and linked to

Motivation

Quick summary

The term "limit" in mathematics is closely related to one of the many senses in which the term "limit" is used in day-to-day English. In day-to-day English, there are two uses of the term "limit":

Limit as something that one approaches, or is headed toward
Limit as a boundary or cap that cannot be crossed or exceeded

The mathematical term "limit" refers to the first of these two meanings. In other words, the mathematical concept of limit is a formalization of the intuitive concept of limit as something that one approaches or is headed toward.

For a function $f$ , the notation:

$lim_{x \to c} f (x)$

is meant to say "the limit, as $x$ approaches $c$ , of the function value $f (x)$ " and thus, the mathematical equality:

$lim_{x \to c} f (x) = L$

is meant to say "the limit, as $x$ approaches $c$ , of the function value $f (x)$ , is $L$ ." In a rough sense, what this means is that as $x$ gets closer and closer to $c$ , $f (x)$ eventually comes, and stays, close enough to $L$ .

Graphical interpretation

The graphical interpretation of " $lim_{x \to c} f (x) = L$ " is that, if we move along the graph $y = f (x)$ of the function $f$ in the plane, then the graph approaches the point $(c, L)$ whether we make $x$ approach $c$ from the left or the right. However, this interpretation works well only if $f$ is continuous on the immediate left and immediate right of $c$ .

This interpretation is sometimes termed the "two finger test" where one finger is used to follow the graph for $x$ slightly less than $c$ and the other finger is used to follow the graph for $x$ slightly greater than $c$ .

Two key ideas

The concept of limit involves two key ideas, both of which help explain why the definition is structured the way it is:

Arbitrarily close: The limit depends on how things behave arbitrarily close to the point involved. The notion of "arbitrarily close" is difficult to quantify non-mathematically, but what it means is that any fixed distance is too much. For instance, if doing $lim_{x \to 2} f (x)$ , we can take points close to 2 such as 2.1, 2.01, 2.001, 2.0001, 2.0000001, 2.000000000000001. Any of these points, viewed in and of itself, is too far from 2 to offer any meaningful information. It is only the behavior in the limit, as we get arbitrarily close, that matters.
Trapping of the function close by: For a function to have a certain limit at a point, it is not sufficient to have the function value come close to that point. Rather, for $lim_{x \to c} f (x) = L$ to hold, it is necessary that for $x$ very close to $c$ , the function value $f (x)$ is trapped close to $L$ . It is not enough that it keeps oscillating between being close to $L$ and being far from $L$ .

Full timed transcript: [SHOW MORE]

0:00:15.549,0:00:19.259

Vipul: Okay, so in this talk, I'm going to go over the basic

0:00:19.259,0:00:24.619 motivation behind the definition of limit, and not so much the

0:00:24.619,0:00:28.099 epsilon-delta definition. That was just an intuitive idea, and a few somewhat

0:00:28.099,0:00:29.680 non-intuitive aspects of that.

0:00:29.680,0:00:36.680 Here I have the notation: "limit as x approaches c of f(x) is L" is

0:00:37.540,0:00:42.079 written like this. Limit ... Under the limit, we write where the

0:00:42.079,0:00:46.180 domain point goes, so x is approaching a value, c, and c could be an

0:00:46.180,0:00:51.059 actual number. x, however, will always be a variable letter. This x

0:00:51.059,0:00:54.519 will not be a number. c could be a number like zero, one, two, three,

0:00:54.519,0:00:55.329 or something.

0:00:55.329,0:01:02.050 f(x). f is the function. We are saying that as x approaches some

0:01:02.050,0:01:06.640 number c, f(x) approaches some number L, and thatâs what this is:

0:01:06.640,0:01:09.030 Limit as x approaches c of f(x) is L.

0:01:09.030,0:01:15.259 Now what does this mean? Roughly what it means is that as x is coming

0:01:15.259,0:01:22.259 closer and closer to c, f(x) is sort of hanging around L. Itâs coming

0:01:22.410,0:01:28.720 closer and closer to L. By the way, there are two senses in which the

0:01:28.720,0:01:32.429 word limit is used in the English language: One meaning its limit in

0:01:32.429,0:01:36.310 this approach sense, which is the mathematical meaning of limit.

0:01:36.310,0:01:41.319 There is another sense in which the word limit is used in the English

0:01:41.319,0:01:46.220 language, which is limit as a boundary or a as a gap or as a bound.

0:01:46.220,0:01:53.160 We may say, there is a limit to how many apples you can eat from the

0:01:53.160,0:01:58.640 food vault or something, and that sense of limit is not used ... for

0:01:58.640,0:02:02.110 that sense of limit you do not use the word "limit" in mathematics. For

0:02:02.110,0:02:05.899 that sense of limit, you use the word bound. In mathematics, we

0:02:05.899,0:02:11.800 reserve the use of the word limit only for this approach sense. Just

0:02:11.800,0:02:18.800 so we donât get confused in mathematics. As I said, the idea is that

0:02:21.120,0:02:25.760 as x approaches c, f(x) approaches L, so as x is coming closer and

0:02:25.760,0:02:29.480 closer to c, the distance between x and c is becoming smaller and

0:02:29.480,0:02:32.740 smaller, the distance between f(x) and L is also roughly becoming

0:02:32.740,0:02:37.980 smaller and smaller. This doesnât quite work unless your function is

0:02:37.980,0:02:41.250 increasing or decreasing near c, so you could have various

0:02:41.250,0:02:46.750 complications with oscillatory functions, so the point is this notion

0:02:46.750,0:02:52.170 doesnât really â¦ it's not very clear what we mean here without further

0:02:52.170,0:02:55.470 elaboration and without a clear definition.

0:02:55.470,0:03:02.470 I'm going to sort of move up toward the definition, and before we go

0:03:02.970,0:03:09.180 there, I want to say, that there is a graphical concept of limit,

0:03:09.180,0:03:13.430 which you may have seen in school. (well, if youâve seen limits in

0:03:13.430,0:03:17.110 school, which hopefully you have. This video is sort of more of a

0:03:17.110,0:03:21.500 review type than learning it for the first time). Let's try to

0:03:21.500,0:03:24.630 understand this from that point of view.

0:03:24.630,0:03:31.630 Let's say, you have a function whose graph looks something like this.

0:03:35.990,0:03:42.990 This is x of c, so this is the value x of c, and this is a graph of

0:03:44.069,0:03:48.310 the function, these curves are the graph of the function, so where x

0:03:48.310,0:03:53.900 is less than c, the graph is along this curve. For x greater than c,

0:03:53.900,0:03:58.120 the graph is this curve. So x less than c, the graph is this curve; x

0:03:58.120,0:04:01.740 greater than c, the graph is this curve. At x equal to c, the value

0:04:01.740,0:04:06.330 is that filled dot.

0:04:06.330,0:04:13.330 You can see from here that as x is approaching c from the left, so if

0:04:13.880,0:04:17.819 you take values of x, which are slightly less than c, the function

0:04:17.819,0:04:23.259 values â¦ so the function, the graph of it, the function values are

0:04:23.259,0:04:27.449 their prospective Y coordinates, so this is x, this is Y, this is the

0:04:27.449,0:04:34.449 graph. Y is f(x). When x is to the initial left of c, the value, Y

0:04:35.749,0:04:42.749 value, the Y approach f(x) value is â¦ are these values, so this or

0:04:44.610,0:04:51.610 this. As x approaches c from the left, the Y values are approaching

0:04:53.699,0:04:57.240 the Y coordinate of this open circle.

0:04:57.240,0:05:04.240 In a sense, if you just were looking at the limit from the left for x

0:05:05.680,0:05:10.830 approaching c from the left, then the limit would be the Y coordinate

0:05:10.830,0:05:16.279 of this open circle. You can also see an x approaches c from the

0:05:16.279,0:05:22.749 right, so approaches from here â¦ the Y coordinate is approaching the Y

0:05:22.749,0:05:29.749 coordinate of this thing, this open circle on top. There are actually

0:05:31.009,0:05:38.009 two concepts here, the left-hand limit is this value. We will call this L1. The right-hand limit is this value,

0:05:45.599,0:05:49.349 L2, so the left-hand limit, which is the notation as limit as x

0:05:49.349,0:05:56.349 approaches c from the left of f(x) is L1, the right-hand limit from the

0:05:58.089,0:06:05.089 right, thatâs plus of f(x), is L2, and the value f of c is some third

0:06:08.059,0:06:15.059 number. We donât know what it is, but f of c, L1, L2, are in this case

0:06:16.770,0:06:18.360 all different.

0:06:18.360,0:06:25.360 What does this mean as far as the limit is concerned? Well, the

0:06:25.900,0:06:28.259 concept of limit is usually a concept of two sides of limit, which

0:06:28.259,0:06:33.419 means that in this case the limit as x approaches c of f(x) does not

0:06:33.419,0:06:36.289 exist because you have a left-hand limit, and you have a right-hand

0:06:36.289,0:06:39.860 limit, and they are not equal to each other. The value, as such,

0:06:39.860,0:06:43.279 doesnât matter, so whether the value exists, what it is, does not

0:06:43.279,0:06:46.379 affect this concept of limit, but the real problem here is that the

0:06:46.379,0:06:48.490 left-hand limit and right-hand limit are not equal. The left-hand

0:06:48.490,0:06:55.490 limit is here; the right-hand limit is up here.

0:06:59.050,0:07:03.499 This graphical interpretation, you see the graphical interpretation is

0:07:03.499,0:07:07.749 sort of that. For the left-hand limit, you basically sort of follow

0:07:07.749,0:07:11.499 the graph on the immediate left and see where it's headed to and you

0:07:11.499,0:07:15.789 get the Y coordinate of that. For the right-hand limit, you follow

0:07:15.789,0:07:21.129 the graph on the right and see where they're headed to, and add the Y

0:07:21.129,0:07:22.240 coordinate of that.

0:07:22.240,0:07:29.240 Let me make an example, where the limit does exist. Let's say you

0:07:42.899,0:07:48.449 have a picture, something like this. In this case, the left-hand limit

0:07:48.449,0:07:52.610 and right-hand limit are the same thing, so this number, but the

0:07:52.610,0:07:55.889 values are different. You could also have a situation where the value

0:07:55.889,0:08:00.460 doesnât exist at all. The function isn't defined at the point, but

0:08:00.460,0:08:03.139 the limits still exist because the left-hand limit and right-hand

0:08:03.139,0:08:04.719 limit are the same.

0:08:04.719,0:08:09.979 Now, all these examples, they're sort of a crude way of putting this

0:08:09.979,0:08:13.710 idea, which is called the two-finger test. You may have heard it in

0:08:13.710,0:08:18.399 some slightly different names. The two-finger test idea is that you

0:08:18.399,0:08:23.929 use one finger to trace the curve on the immediate left and see where

0:08:23.929,0:08:28.259 thatâs headed to, and use another finger to trace the curve on the

0:08:28.259,0:08:33.640 immediate right and see where thatâs headed to, and if your two

0:08:33.640,0:08:38.270 fingers can meet each other, then the place where they meet, the Y

0:08:38.270,0:08:41.870 coordinate of that, is the limit. If, however, they do not come to

0:08:41.870,0:08:46.940 meet each other, which happens in this case, one of them is here, one

0:08:46.940,0:08:51.120 is here, and then the limit doesnât exist because the left-hand limit

0:08:51.120,0:08:53.509 and right-hand limit are not equal.

0:08:53.509,0:08:59.819 This, hopefully, you have seen in great detail where youâve done

0:08:59.819,0:09:05.779 limits in detail in school. However, what I want to say here is that

0:09:05.779,0:09:11.850 this two-finger test is not really a good definition of limit. Whatâs

0:09:11.850,0:09:13.600 the problem? The problem is that you could have really crazy

0:09:13.600,0:09:18.790 function, and it's really hard to move your finger along the graph of

0:09:18.790,0:09:25.220 the function. If the function sort of jumps around a lot, it's really

0:09:25.220,0:09:29.440 hard, and it doesnât really solve any problem. It's not really a

0:09:29.440,0:09:35.100 mathematically pure thing. It's like trying to answer the

0:09:35.100,0:09:39.540 mathematical question using a physical description, which is sort of

0:09:39.540,0:09:41.579 the wrong type of answer.

0:09:41.579,0:09:45.610 While this is very good for a basic intuition for very simple types of

0:09:45.610,0:09:50.040 functions, it's not actually the correct idea of limit. What kind of

0:09:50.040,0:09:56.990 things could give us trouble? Why do we need to define our

0:09:56.990,0:10:03.209 understanding of limit? The main thing is functions which have a lot

0:10:03.209,0:10:07.980 of oscillation. Let me do an example.

0:10:07.980,0:10:14.980 I'm now going to write down a type of function where, in fact, you

0:10:18.220,0:10:21.899 have to develop a pure cut concept of limit to be able to answer this

0:10:21.899,0:10:28.899 question precisely. This is a graph of a function, sine 1 over x.

0:10:28.959,0:10:32.920 Now this looks a little weird. It's not 1 over sine x; that would

0:10:32.920,0:10:39.920 just equal secant x. It's not that. It's sine of 1 over x, and this

0:10:44.879,0:10:50.220 function itself is not defined at x equals zero, but just the fact

0:10:50.220,0:10:52.660 that thatâs not defined, isn't good enough for us to say the limit

0:10:52.660,0:10:55.139 doesn't [inaudible 00:10:36] we actually have to try to make a picture

0:10:55.139,0:10:57.660 of this and try to understand what the limit is here.

0:10:57.660,0:11:04.660 Let's first make the picture of sine x. Sine-x looks like that. How

0:11:12.560,0:11:19.560 will sine 1 over x look? Let's start of where x is nearly infinity.

0:11:20.100,0:11:25.759 When x is very large positive, 1 over x is near zero, slightly

0:11:25.759,0:11:30.660 positive, just slightly bigger than zero, and sine 1 over x is

0:11:30.660,0:11:36.879 therefore slightly positive. It's like here. It's going to start up

0:11:36.879,0:11:42.810 with an S [inaudible 00:11:21] at zero. Then it's going to sort of go

0:11:42.810,0:11:49.420 this path, but much more slowly, each one, then it's going to go this

0:11:49.420,0:11:56.420 path, but in reverse, so like that. Then it's going to go this path,

0:11:57.149,0:12:00.740 but now it does all these oscillations, all of these oscillations. It

0:12:00.740,0:12:03.569 has to go faster and faster.

0:12:03.569,0:12:10.569 For instance, this is pi, this 1 over pi, then this is 2 pi, this

0:12:12.329,0:12:16.990 number is 1 over 2 pi, then the then next time it reaches zero will be

0:12:16.990,0:12:21.160 1 over 3 pi, and so on. Whatâs going to happen is that near zero it's

0:12:21.160,0:12:24.579 going to be crazily oscillating between minus 1, and 1. The frequency

0:12:24.579,0:12:29.170 of the oscillation keeps getting faster and faster as you come closer

0:12:29.170,0:12:34.050 and closer to zero. The same type of picture on the left side as

0:12:34.050,0:12:40.360 well; it's just that it's an odd function. It's this kind of picture.

0:12:40.360,0:12:47.360 I'll make a bigger picture here ... I'll make a bigger picture on another

0:12:53.649,0:13:00.649 one. all of these oscillation should be between minus 1 and 1, and we

0:13:22.439,0:13:29.399 get faster so we get faster and faster, and now my pen is too thick.

0:13:29.399,0:13:31.600 It's the same, even if you used your finger instead of the pen to

0:13:31.600,0:13:38.600 place it, it would be too thick, it's called the thick finger problem.

0:13:38.850,0:13:45.060 Iâm not being very accurate here, but just the idea. The pen or

0:13:45.060,0:13:49.199 finger is too thick, but actually, there's a very thin line, and it's

0:13:49.199,0:13:52.519 an infinitely thin line of the graph, which goes like that.

0:13:52.519,0:13:59.519 Let's get back to our question: What is limit as x approaches zero,

0:14:02.699,0:14:09.699 sine 1 over x. I want you to think about this a bit. Think about like

0:14:13.439,0:14:18.050 the finger test. You move your finger around, move it like this,

0:14:18.050,0:14:21.579 this, this â¦ you're sort of getting close to here but still not quite

0:14:21.579,0:14:28.579 reaching it. It's â¦ where are you headed? It's kind of a little

0:14:31.610,0:14:36.879 unclear. Notice, it's not that just because we plug in zero doesnât

0:14:36.879,0:14:39.170 make sense, the limit doesn't... Thatâs not the issue. The issue is

0:14:39.170,0:14:43.249 that after you make the graph, it's unclear whatâs happening.

0:14:43.249,0:14:49.329 One kind of logic is that the other limit is zero? Why? Well, it's

0:14:49.329,0:14:52.949 kind of balance around here. It's a bit above and below, and it keeps

0:14:52.949,0:14:59.949 coming close to zero. That any number of the form x is 1 over N pi,

0:15:00.329,0:15:07.329 sine 1 over x is zero. It keeps coming close to zero. As x

0:15:07.990,0:15:12.459 approaches zero, this number keeps coming close to zero.

0:15:12.459,0:15:17.449 If you think of limit as something thatâs approaching, then as x

0:15:17.449,0:15:24.449 approaches zero, sine 1 over x is sort of coming close to zero, is it?

0:15:31.230,0:15:36.550 It's definitely coming near zero, right? Anything you make around

0:15:36.550,0:15:41.920 zero, any small â¦ this you make around zero, the graph is going to

0:15:41.920,0:15:42.399 enter that.

0:15:42.399,0:15:47.269 On the other hand, it's not really staying close to zero. It's kind of

0:15:47.269,0:15:50.300 oscillating with the minus 1 and 1. However, smaller interval you

0:15:50.300,0:15:54.540 take around zero on the x thing, the function is oscillating between

0:15:54.540,0:15:57.600 minus 1 and 1. It's not staying faithful to zero.

0:15:57.600,0:16:02.249 Now you have kind of this question: What should be the correct

0:16:02.249,0:16:09.249 definition of this limit? Should it mean that it approaches the

0:16:10.029,0:16:15.100 point, but maybe goes in and out, close and far? Or should it mean it

0:16:15.100,0:16:18.879 approaches and stays close to the point? That is like a judgment you

0:16:18.879,0:16:22.629 have to make in the definition, and it so happens that people who

0:16:22.629,0:16:28.639 tried defining this chose the latter idea; that is, it should come

0:16:28.639,0:16:33.089 close and stay close. So thatâs actually key idea number two we have

0:16:33.089,0:16:38.290 here the function â¦ for the function to have a limit at the point, the

0:16:38.290,0:16:43.639 function needs to be trapped near the limit, close to the point in the

0:16:43.639,0:16:45.079 domain.

0:16:45.079,0:16:49.459 This is, therefore, it doesnât have a limit at zero because the

0:16:49.459,0:16:54.420 function is oscillating too widely. You cannot trap it. You cannot

0:16:54.420,0:17:01.059 trap the function values. You cannot say thatâ¦ you cannot trap the

0:17:01.059,0:17:08.059 function value, say, in this small horizontal strip near zero. You

0:17:08.319,0:17:11.650 cannot trap in the area, so that means the limit cannot be zero, but

0:17:11.650,0:17:15.400 the same logic works anywhere else. The limit cannot be half, because

0:17:15.400,0:17:20.440 you cannot trap the function in a small horizontal strip about half

0:17:20.440,0:17:22.130 whereas x approaches zero.

0:17:22.130,0:17:26.440 We will actually talk about this example in great detail in our future

0:17:26.440,0:17:30.330 with you after we've seen the formal definition, but the key idea you

0:17:30.330,0:17:33.890 need to remember is that the function doesnât just need to come close

0:17:33.890,0:17:37.340 to the point of its limit. It actually needs to stay close. It needs

0:17:37.340,0:17:41.050 to be trapped near the point.

0:17:41.050,0:17:44.810 The other important idea regarding limits is that the limit depends

0:17:44.810,0:17:50.370 only on the behavior very, very close to the point. What do I mean by

0:17:50.370,0:17:56.580 very, very close? If you were working it like, the real goal, you may

0:17:56.580,0:18:02.300 say, it's like, think of some really small number and you say that

0:18:02.300,0:18:07.050 much distance from it. Let's say I want to get the limit as x

0:18:07.050,0:18:14.050 approaches 2...I'll just write it here. I want to get, let's say,

0:18:23.520,0:18:30.520 limit has x approaches 2 of some function, we may say, well, we sort

0:18:30.550,0:18:37.550 of â¦ whatâs close enough? Is 2.1 close enough? No, thatâs too far.

0:18:38.750,0:18:43.380 What about 2.0000001? Is that close enough?

0:18:43.380,0:18:47.420 Now, if you werenât a mathematician, you would probably say, "Yes,

0:18:47.420,0:18:54.420 this is close enough." The difference is like ... so it's

0:18:57.040,0:19:04.040 10^{-7}. It's really only close to 2 compared to our usual sense of

0:19:12.990,0:19:16.670 numbers, but as far as mathematics is concerned, both of these numbers

0:19:16.670,0:19:21.110 are really far from 2. Any individual number that is not 2 is very

0:19:21.110,0:19:22.130 far from 2.

0:19:22.130,0:19:29.130 What do I mean by that, well, think back to one of our

0:19:29.670,0:19:36.670 pictures. Here's a picture. Supposed I take some points. Let's say

0:19:41.970,0:19:47.640 this is 2, and suppose I take one point here, which is really close to

0:19:47.640,0:19:50.970 2, and I just change the value of the function at that point. I

0:19:50.970,0:19:55.200 change the value of the function at that point, or I just change the

0:19:55.200,0:19:59.990 entire picture of the graph from that point rightward. I just take

0:19:59.990,0:20:05.940 this picture, and I change it to, let's say â¦ so I replace this

0:20:05.940,0:20:11.410 picture by that picture, or I replace the picture by some totally new

0:20:11.410,0:20:15.250 picture like that picture. I just change the part of the graph to the

0:20:15.250,0:20:21.440 right of some point, like 2.00001, whatever. Will that effect the

0:20:21.440,0:20:25.770 limit at 2? No, because the limit at 2 really depends only on the

0:20:25.770,0:20:27.520 behavior if you're really, really close.

0:20:27.520,0:20:32.040 If you take any fixed point, which is not 2, and you change the

0:20:32.040,0:20:35.000 behavior sort of at this time that point or farther away than that

0:20:35.000,0:20:42.000 point, then the behavior close to 2 doesnât get affected. Thatâs the

0:20:42.820,0:20:46.660 other key idea here. Actually I did these in [inaudible 00:20:30].

0:20:46.660,0:20:52.060 Thatâs how it is coming, actually, but I'll just say it again.

0:20:52.060,0:20:56.570 The limit depends on the behavior arbitrarily close to the point. It

0:20:56.570,0:21:00.210 doesnât depend on the behavior at any single specific other point. It

0:21:00.210,0:21:06.910 just depends on the behavior as you approach the point and any other

0:21:06.910,0:21:11.330 point is far away. It's only sort of together that all the other

0:21:11.330,0:21:16.230 points matter, and it's only them getting really close that

0:21:16.230,0:21:19.790 matters. The other thing is that the function actually needs to be

0:21:19.790,0:21:26.790 tracked near the point for the limit notion to be true. This type of

0:21:26.860,0:21:29.650 picture where it's oscillating between minus 1 and 1, however close

0:21:29.650,0:21:35.150 you get to zero, keeps oscillating, and so you cannot trap it around

0:21:35.150,0:21:40.590 any point. You cannot trap the function value in any small enough

0:21:40.590,0:21:47.590 strip. In that case, the limit doesnât exist. In subsequent videos,

0:21:48.550,0:21:54.630 we'll see Epsilon definition, we'll do a bit of formalism to that, and

0:21:54.630,0:22:00.640 then we'll come back to some of these issues later with the formal

0:22:00.640,0:22:01.870

understanding.

Definition for finite limit for function of one variable

Two-sided limit

Suppose $f$ is a function of one variable and $c \in R$ is a point such that $f$ is defined to the immediate left and immediate right of $c$ (note that $f$ may or may not be defined at $c$ ). In other words, there exists some value $t > 0$ such that $f$ is defined on $(c - t, c + t) ∖ {c} = (c - t, c) \cup (c, c + t)$ .

For a given value $L \in R$ , we say that:

$lim_{x \to c} f (x) = L$

if the following holds (the single sentence is broken down into multiple points to make it clearer):

For every $ε > 0$ (the symbol $ε$ is a Greek lowercase letter pronounced "epsilon")
there exists $δ > 0$ such that (the symbol $δ$ is a Greek lowercase letter pronounced "delta")
for all $x \in R$ satisfying $0 < | x - c | < δ$ (explicitly, $x \in (c - δ, c) \cup (c, c + δ) = (c - δ, c + δ) ∖ {c}$ ),
we have $| f (x) - L | < ε$ (explicitly, $f (x) \in (L - ε, L + ε)$ ).

The limit (also called the two-sided limit) $lim_{x \to c} f (x)$ is defined as a value $L \in R$ such that $lim_{x \to c} f (x) = L$ . By the uniqueness theorem for limits, there is at most one value of $L \in R$ for which $lim_{x \to c} f (x) = L$ . Hence, it makes sense to talk of the limit when it exists.

Full timed transcript: [SHOW MORE]

0:00:15.809,0:00:20.490 Vipul: In this talk, I'm going to introduce the definition, the formal epsilon delta definition

0:00:20.490,0:00:24.669 of a two-sided limit for a function of a one variable, that's called f.

0:00:24.669,0:00:31.349 I'm going to assume there is a point c and c doesn't actually have to be in the domain of f.

0:00:31.349,0:00:38.030 Thus f doesn't have to be defined at c for this notion to make sense rather f is defined around c.

0:00:38.030,0:00:44.909 What that means is f is defined on some open set containing c.

0:00:51.009,0:01:03.009 Let's make a picture here so you have c, c + t, c -- t.

0:01:03.040,0:01:11.040 What this is saying is there is some t probably small enough so that the function is defined

0:01:12.549,0:01:18.590 in here and may be it's not defined at the point c.

0:01:18.590,0:01:31.590 This set for some t>0. The function is defined on the immediate left of c and it is defined

0:01:31.999,0:01:34.770 on the immediate right of c.

0:01:34.770,0:01:38.890 We need that in order to make sense of what I'm going to say.

0:01:38.890,0:01:44.590 We say that limit as x approaches c of f(x) is L where L is some other real number or

0:01:44.590,0:01:49.679 maybe it's the same real number [as c], so we say this limit equals L, now I'll write the definition

0:01:49.679,0:01:56.679 in multiple lines just to be clear about the parts of the definition.

0:01:56.770,0:02:39.770 For every epsilon > 0. This is epsilon. There exists delta > 0 such that for all x in R satisfying...what?

0:02:41.070,0:02:45.070 Rui: Satisfying |x -- c| ...

0:02:45.659,0:02:53.659 Vipul: [|x-c|] should be not equal to zero so zero less than, exclude the point c itself,

0:02:54.810,0:02:56.930 less than delta. What do we have?

0:02:56.930,0:02:59.459 Rui: We have y is within.

0:02:59.459,0:03:04.260 Vipul: Well y is just f(x).

0:03:04.260,0:03:10.290 Rui: f(x_0)

0:03:14.290,0:03:16.819 Vipul: Well f(x) minus the claimed limit is?

0:03:17.219,0:03:18.040 Rui: L.

0:03:18.640,0:03:22.890 Vipul: You're thinking of continuity which is a little different but here we have this less than?

0:03:22.890,0:03:24.569 Rui: Epsilon.

0:03:24.569,0:03:37.569 Vipul: Epsilon. Let me now just re-write these conditions in interval notation.

0:03:37.830,0:03:40.031 What is this saying x in what interval? [ANSWER!]

0:03:40.040,0:03:43.519 Rui: c +- ...

0:03:43.519,0:03:49.840 Vipul: c- delta to c + delta excluding the point c itself, that is what 0 < [|x -- c|] is telling us.

0:03:49.840,0:03:56.530 It is telling us x is within delta distance of c, but it is not including c.

0:03:56.530,0:04:10.530 Another way of writing this is (c -- delta,c) union (c, c + delta)

0:04:12.810,0:04:19.340 x is either on immediate delta left of c or it's on the immediate delta right of c.

0:04:21.040,0:04:31.040 You do something similar on the f(x) side so what interval is this saying, f(x) is in what? [ANSWER!]

0:04:31.720,0:04:35.930 Rui: L -- epsilon, L + epsilon.

0:04:35.930,0:04:42.930 Vipul: Awesome. Instead of writing the conditions in this inequality form you could have written

0:04:43.919,0:04:47.590 them in this form, so instead of writing this you could have written this or this, instead

0:04:47.590,0:04:49.580 of writing this you could have written this.

0:04:50.080,0:04:59.500 If this statement is true, the way you read this is you say limit as x approaches c of f(x) equals L.

0:04:59.500,0:05:07.500 Okay. Now how do we define the limit?

0:05:11.169,0:05:18.169 It's the number L for which the above holds. This should be in quotes.

0:05:22.009,0:05:29.009 If a number L exists for which.

0:05:34.220,0:05:41.220 Now what would you need in order to show that this definition makes sense?

0:05:47.919,0:05:52.919 Rui: I don't think I understand your question.

0:06:03.090,0:06:09.090 Vipul: What I mean is, what I wanted to ask was what would you need to prove in order

0:06:09.990,0:06:14.889 to say the notion of the limit makes sense? Well, you need to show that there is uniqueness here.

0:06:14.740,0:06:19.080 It cannot happen that the limit is some number L and the limit is another number M so you

0:06:19.080,0:06:20.539 need to show uniqueness.

0:06:20.539,0:06:27.330 You need to show that if this holds for one number L it cannot also hold for another number.

0:06:27.330,0:06:32.050 Once you have shown that then it you could define it like this.

0:06:32.050,0:06:38.440 Now I should say "if it exists."

0:06:38.440,0:06:42.120 What I'm saying is that there is a uniqueness theorem which we will prove some other time.

0:06:42.120,0:06:49.120 Which says that if this is true for one number it cannot be true for any other number so

0:06:49.440,0:06:54.740 this statement is true for at the most one value of L and if there is such a value of

0:06:54.740,0:06:55.050

L that's called the limit.

Note: Although the definition customarily uses the letters $ε$ and $δ$ , any other letters can be used, as long as these letters are different from each other and from the letters already in use. The reason for sticking to a standard letter choice is that it reduces cognitive overload.

Left hand limit

Suppose $f$ is a function of one variable and $c \in R$ is a point such that $f$ is defined on the immediate left of $c$ (note that $f$ may or may not be defined at $c$ ). In other words, there exists some value $t > 0$ such that $f$ is defined on $(c - t, c)$ .

For a given value $L \in R$ , we say that:

$lim_{x \to c^{-}} f (x) = L$

if the following holds (the single sentence is broken down into multiple points to make it clearer):

For every $ε > 0$
there exists $δ > 0$ such that
for all $x \in R$ satisfying $0 < c - x < δ$ (explicitly, $x \in (c - δ, c)$ ),
we have $| f (x) - L | < ε$ (explicitly, $f (x) \in (L - ε, L + ε)$ .

The left hand limit (acronym LHL) $lim_{x \to c^{-}} f (x)$ is defined as a value $L \in R$ such that $lim_{x \to c^{-}} f (x) = L$ . By the uniqueness theorem for limits (one-sided version), there is at most one value of $L \in R$ for which $lim_{x \to c^{-}} f (x) = L$ . Hence, it makes sense to talk of the left hand limit when it exists.

Right hand limit

Suppose $f$ is a function of one variable and $c \in R$ is a point such that $f$ is defined on the immediate right of $c$ (note that $f$ may or may not be defined at $c$ ). In other words, there exists some value $t > 0$ such that $f$ is defined on $(c, c + t)$ .

For a given value $L \in R$ , we say that:

$lim_{x \to c^{+}} f (x) = L$

if the following holds (the single sentence is broken down into multiple points to make it clearer):

For every $ε > 0$
there exists $δ > 0$ such that
for all $x \in R$ satisfying $0 < x - c < δ$ (explicitly, $x \in (c, c + δ)$ ),
we have $| f (x) - L | < ε$ (explicitly, $f (x) \in (L - ε, L + ε)$ .

The right hand limit (acronym RHL) $lim_{x \to c^{+}} f (x)$ is defined as a value $L \in R$ such that $lim_{x \to c^{+}} f (x) = L$ . By the uniqueness theorem for limits (one-sided version), there is at most one value of $L \in R$ for which $lim_{x \to c^{+}} f (x) = L$ . Hence, it makes sense to talk of the right hand limit when it exists.

Relation between the limit notions

The two-sided limit exists if and only if (both the left hand limit and right hand limit exist and they are equal to each other).

Definition of finite limit for function of one variable in terms of a game

The formal definitions of limit, as well as of one-sided limit, can be reframed in terms of a game. This is a special instance of an approach that turns any statement with existential and universal quantifiers into a game.

Two-sided limit

Consider the limit statement, with specified numerical values of $c$ and $L$ and a specified function $f$ :

$lim_{x \to c} f (x) = L$

Note that there is one trivial sense in which the above statement can be false, or rather, meaningless, namely, that $f$ is not defined on the immediate left or immediate right of $c$ . In that case, the limit statement above is false, but moreover, it is meaningless to even consider the notion of limit.

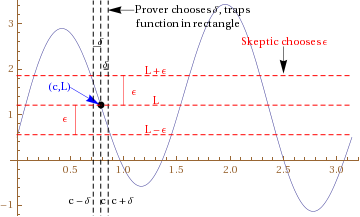
The game is between two players, a Prover whose goal is to prove that the limit statement is true, and a Skeptic (also called a Verifier or sometimes a Disprover) whose goal is to show that the statement is false. The game has three moves:

First, the skeptic chooses $ε > 0$ , or equivalently, chooses the target interval $(L - ε, L + ε)$ .
Then, the prover chooses $δ > 0$ , or equivalently, chooses the interval $(c - δ, c + δ) ∖ {c}$ .
Then, the skeptic chooses a value $x$ satisfying $0 < | x - c | < δ$ , or equivalently, $x \in (c - δ, c + δ) ∖ {c}$ , which is the same as $(c - δ, c) \cup (c, c + δ)$ .

Now, if $| f (x) - L | < ε$ (i.e., $f (x) \in (L - ε, L + ε)$ ), the prover wins. Otherwise, the skeptic wins (see the subtlety about the domain of definition issue below the picture).

We say that the limit statement

$lim_{x \to c} f (x) = L$

is true if the prover has a winning strategy for this game. The winning strategy for the prover basically constitutes a strategy to choose an appropriate $δ$ in terms of the $ε$ chosen by the skeptic. Thus, it is an expression of $δ$ as a function of $ε$ .

We say that the limit statement

$lim_{x \to c} f (x) = L$

is false if the skeptic has a winning strategy for this game. The winning strategy for the skeptic involves a choice of $ε$ , and a strategy that chooses a value of $x$ (constrained in the specified interval) based on the prover's choice of $δ$ .

Slight subtlety regarding domain of definition: The domain of definition issue leads to a couple of minor subtleties:

A priori, it is possible that the $x$ chosen by the skeptic is outside the domain of $f$ , so it does not make sense to evaluate $f (x)$ . In the definition given above, this would lead to the game being won by the skeptic. In particular, if $f$ is not defined on the immediate left or right of $c$ , the skeptic can always win by picking $x$ outside the domain.
It may make sense to restrict discussion to the cases where f is defined on the immediate left or right of c. Explicitly, we assume that f is defined on the immediate left and immediate right, i.e., there exists t>0 such that f is defined on the interval (c−t,c+t)∖{c}. In this case, it does not matter what rule we set regarding the case that the skeptic picks x outside the domain. To simplify matters, we could alter the rules in any one of the following ways, and the meaning of limit would remain the same as in the original definition:
- We could require (as part of the game rules) that the prover pick $δ$ such that $(c - δ, c + δ) ∖ {c} \subseteq d o m f$ . This pre-empts the problem of picking $x$ -values outside the domain.
- We could require (as part of the game rules) that the skeptic pick $x$ in the domain, i.e., pick $x$ with $0 < | x - c | < δ$ and $x \in d o m f$ .
- We could alter the rule so that if the skeptic picks $x$ outside the domain, the prover wins (instead of the skeptic winning).

Non-existence of limit

The statement $lim_{x \to c} f (x)$ does not exist could mean one of two things:

$f$ is not defined around $c$ , i.e., there is no $t > 0$ for which $f$ is defined on $(c - t, c + t) ∖ {c}$ . In this case, it does not even make sense to try taking a limit.
$f$ is defined around $c$ , around $c$ , i.e., there is $t > 0$ for which $f$ is defined on $(c - t, c + t) ∖ {c}$ . So, it does make sense to try taking a limit. However, the limit still does not exist.

The formulation of the latter case is as follows:

For every
$L \in R$
, there exists
$ε > 0$
such that for every
$δ > 0$
, there exists
$x$
satisfying
$0 < | x - c | < δ$
and such that
$| f (x) - L | \geq ε$
.

We can think of this in terms of a slight modification of the limit game, where, in our modification, there is an extra initial move by the prover to propose a value $L$ for the limit. The limit does not exist if the skeptic has a winning strategy for this modified game.

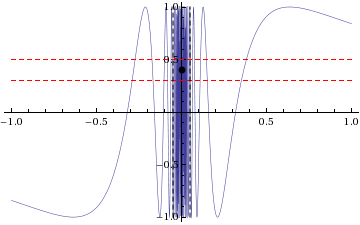
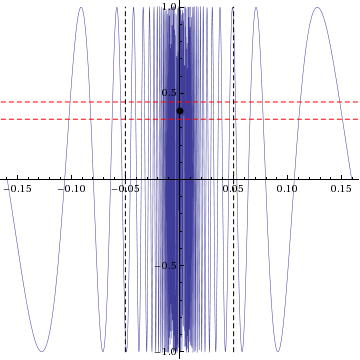
An example of a function that does not have a limit at a specific point is the sine of reciprocal function. Explicitly, the limit:

$lim_{x \to 0} \sin (\frac{1}{x})$

does not exist. The skeptic's winning strategy is as follows: regardless of the $L$ chosen by the prover, pick a fixed $ε < 1$ (independent of $L$ , so $ε$ can be decided in advance of the game -- note that the skeptic could even pick $ε = 1$ and the strategy would still work). After the prover has chosen a value $δ$ , find a value $x \in (0 - δ, 0 + δ) ∖ {0}$ such that the $\sin (1 / x)$ function value lies outside $(L - ε, L + ε)$ . This is possible because the interval $(L - ε, L + ε)$ has width $2 ε$ , hence cannot cover the entire interval $[- 1, 1]$ , which has width 2. However, the range of the $\sin (1 / x)$ function on $(0 - δ, 0 + δ) ∖ {0}$ is all of $[- 1, 1]$ .

Conceptual definition and various cases

Formulation of conceptual definition

Below is the conceptual definition of limit. Suppose $f$ is a function defined in a neighborhood of the point $c$ , except possibly at the point $c$ itself. We say that:

$lim_{x \to c} f (x) = L$

if:

For every choice of neighborhood of $L$ (where the term neighborhood is suitably defined)
there exists a choice of neighborhood of $c$ (where the term neighborhood is suitably defined) such that
for all $x \neq c$ that are in the chosen neighborhood of $c$
$f (x)$ is in the chosen neighborhood of $L$ .

Functions of one variable case

The following definitions of neighborhood are good enough to define limits.

For points in the interior of the domain, for functions of one variable: We can take an open interval centered at the point. For a point $c$ , such an open interval is of the form $(c - t, c + t), t > 0$ . Note that if we exclude the point $c$ itself, we get $(c - t, c) \cup (c, c + t)$ .
For the point $+ \infty$ , for functions of one variable: We take intervals of the form $(a, \infty)$ , where $a \in R$ .
For the point $- \infty$ , for functions of one variable: We can take interval of the form $(- \infty, a)$ , where $a \in R$ .

We can now list the nine cases of limits, combining finite and infinite possibilities:

Case	Definition
$lim_{x \to c} f (x) = L$	For every $ε > 0$ , there exists $δ > 0$ such that for all $x$ satisfying $0 < \| x - c \| < δ$ (i.e., $x \in (c - δ, c) \cup (c, c + δ)$ ), we have $\| f (x) - L \| < ε$ (i.e., $f (x) \in (L - ε, L + ε)$ ).
$lim_{x \to c} f (x) = - \infty$	For every $a \in R$ , there exists $δ > 0$ such that for all $x$ satisfying $0 < \| x - c \| < δ$ (i.e., $x \in (c - δ, c) \cup (c, c + δ)$ ), we have $f (x) < a$ (i.e., $f (x) \in (- \infty, a)$ ).
$lim_{x \to c} f (x) = \infty$	For every $a \in R$ , there exists $δ > 0$ such that for all $x$ satisfying $0 < \| x - c \| < δ$ (i.e., $x \in (c - δ, c) \cup (c, c + δ)$ ), we have $f (x) > a$ (i.e., $f (x) \in (a, \infty)$ ).
$lim_{x \to - \infty} f (x) = L$	For every $ε > 0$ , there exists $a \in R$ such that for all $x$ satisfying $x < a$ (i.e., $x \in (- \infty, a)$ ), we have $\| f (x) - L \| < ε$ (i.e., $f (x) \in (L - ε, L + ε)$ ).
$lim_{x \to - \infty} f (x) = - \infty$	For every $b \in R$ , there exists $a \in R$ such that for all $x$ satisfying $x < a$ (i.e., $x \in (- \infty, a)$ ), we have $f (x) < b$ (i.e., $f (x) \in (- \infty, b)$ ).
$lim_{x \to - \infty} f (x) = \infty$	For every $b \in R$ , there exists $a \in R$ such that for all $x$ satisfying $x < a$ (i.e., $x \in (- \infty, a)$ ), we have $f (x) > b$ (i.e., $f (x) \in (b, \infty)$ ).
$lim_{x \to \infty} f (x) = L$	For every $ε > 0$ , there exists $a \in R$ such that for all $x$ satisfying $x > a$ (i.e., $x \in (a, \infty)$ ), we have $\| f (x) - L \| < ε$ (i.e., $f (x) \in (L - ε, L + ε)$ ).
$lim_{x \to \infty} f (x) = - \infty$	For every $b \in R$ , there exists $a \in R$ such that for all $x$ satisfying $x > a$ (i.e., $x \in (a, \infty)$ ), we have $f (x) < b$ (i.e., $f (x) \in (- \infty, b)$ ).
$lim_{x \to \infty} f (x) = \infty$	For every $b \in R$ , there exists $a \in R$ such that for all $x$ satisfying $x > a$ (i.e., $x \in (a, \infty)$ ), we have $f (x) > b$ (i.e., $f (x) \in (b, \infty)$ ).

Limit of sequence versus real-sense limit

Fill this in later

Real-valued functions of multiple variables case

We consider the multiple input variables as a vector input variable, as the definition is easier to frame from this perspective.

The correct notion of neighborhood is as follows: for a point $\bar{c}$ , we define the neighborhood parametrized by a positive real number $r$ as the open ball of radius $r$ centered at $\bar{c}$ , i.e., the set of all points $\bar{x}$ such that the distance from $\bar{x}$ to $\bar{c}$ is less than $r$ . This distance is the same as the norm of the difference vector $\bar{x} - \bar{c}$ . The norm is sometimes denoted $| \bar{x} - \bar{c} |$ . This open ball is sometimes denoted $B_{r} (\bar{c})$ .

Suppose $f$ is a real-valued (i.e., scalar) function of a vector variable $\bar{x}$ . Suppose $\bar{c}$ is a point such that $f$ is defined "around" $\bar{c}$ , except possibly at $\bar{c}$ . In other words, there is an open ball centered at $\bar{c}$ such that $f$ is defined everywhere on that open ball, except possibly at $\bar{c}$ .

With these preliminaries out of the way, we can define the notion of limit. We say that:

$lim_{\bar{x} \to \bar{c}} f (\bar{x}) = L$

if the following holds:

For every $ε > 0$
there exists $δ > 0$ such that
for all $\bar{x}$ satisfying $0 < | \bar{x} - \bar{c} | < δ$ (i.e., $\bar{x}$ is in a ball of radius $δ$ centered at $\bar{c}$ but not the point $\bar{c}$ itself -- note that the $| \cdot |$ notation is for the norm, or length, of a vector)
we have $| f (\bar{x}) - L | < ε$ . Note that $f (\bar{x})$ and $L$ are both scalars, so the $| \cdot |$ here is the usual absolute value function.