Point of local extremum implies critical point

This article describes a test that can be used to determine whether a point in the domain of a function gives a point of local, endpoint, or absolute (global) maximum or minimum of the function, and/or to narrow down the possibilities for points where such maxima or minima occur.
View a complete list of such tests

Statement

Suppose $f$ is a function of one variable and $c$ is a point in the interior of the domain of $f$ (i.e., $f$ is defined on an open interval containing $c$).

Suppose further that $c$ is a point of local extremum for $f$, i.e., $f$ attains a local extreme value (either a local maximum or a local minimum) at $c$.

Then, $c$ is a critical point for $f$, i.e., either the derivative $f'(c)$ equals zero or the derivative $f'(c)$ does not exist.

Note that the $f'(c)$ not existing case could occur in either of these ways: one or both the one-sided derivatives of $f$ at $c$ not existing, or both one-sided derivatives of $f$ at $c$ existing but being unequal.

Related facts

• Point of local extremum implies critical point for a function of multiple variables

Significance

General comments

The main significance of this result is that it mostly reduces an optimization problem (finding a maximum or minimum) to an equation-solving problem (finding when an expression is zero).

The reduction isn't perfect, in that it has the following caveats:

• The result is only a one-sided implication. Any point of local extremum is a critical point, but it's possible for a critical point to not be a point of local extremum. Even so, in many cases, the set of critical points is already small enough and manageable enough.
• This result is about local extrema, not absolute / global extrema. There may be many points of local extremum that aren't points of absolute extremum. Moreover, there could be many cases where an absolute extremum doesn't exist; for instance, for a function that is going to infinity as the input goes to infinity or to a point of discontinuity (such as $x\mapsto 1/x$ as $x\to 0^{+}$ and $x\to 0^{-}$. With that being said, in many cases, we can rule out limiting behaviors of that sort, and the set of points of local extremum is small enough that it's feasible to find the absolute extremum by looking among them.

Qualitative and existential significance

Type of function for which we are interested in understanding local extrema	Maximum number of points of local extremum	Inference	Example
polynomial function of degree $d$	$d-1$	The derivative is a polynomial of degree $d-1$, so it is defined everywhere and has at most $d-1$ real roots. Therefore, there are at most $d-1$ critical points (all of the "derivative equals zero" type, none of the "derivative is undefined" type) and therefore at most $d-1$ points of local extremum for the function.	$x^{3}-3x$ of degree $d=3$ has $3-1=2$ critical points: the two solutions to $3x^{2}-3=0$, namely $x=-1$ and $x=1$. Both of these turn out to be points of local extremum.
rational function in simplified form with numerator degree $d_{1}$ and denominator degree $d_{2}$	$d_{1}+d_{2}-1$	The derivative is a rational function with numerator degree at most $d_{1}+d_{2}-1$ and denominator a square of the original denominator. The only way for the derivative to be undefined is for the denominator to be zero, in which case the denominator of the original rational function would also be zero, so that the original rational function would also be undefined. Therefore, the derivative exists everywhere that the function is defined, and the only critical points are cases where the derivative is zero. Since the numerator is a polynomial of degree at most $d_{1}+d_{2}-1$, there are therefore at most $d_{1}+d_{2}-1$ critical points, and therefore at most $d_{1}+d_{2}-1$ points of local extremum.	$x/(x^{2}+1)$ with $d_{1}=1,d_{2}=2$ has derivative $(1-x^{2})/(x^{2}+1)^{2}$ and has $1+2-1=2$ critical points, namely the solutions to $1-x^{2}=0$, so $x=-1$ and $x=1$. Both of these turn out to be points of local extremum.

Computational feasibility significance

As a general rule, for any family of functions ${\mathcal {F}}$ for which we know how to find the roots of any function in the family (i.e., the points where the function is zero), we have a strategy to find critical points (and therefore points of local extremum) for any function whose derivative is in ${\mathcal {F}}$.

In particular, since we know how to find the roots of polynomials of degree 1 (linear polynomial) or 2 (quadratic polynomial), we can find the critical points of any degree 2 (quadratic) or degree 3 (cubic) function, as well as of any rational function with a linear numerator and quadratic denominator.

From the perspective of numerical approximation, any method for numerically approximating the roots of a function in a family ${\mathcal {F}}$ can become a method for finding the critical points (and hence, the points of local extremum) of a function whose derivative is in ${\mathcal {F}}$. Some of these translations are below:

Root-finding method	Corresponding optimization method
Newton's method for root-finding for a function of one variable	Newton's method for optimization of a function of one variable

Facts used

Statement of facts

Fact no. (for reference in proof)	Statement	Assumption about one-sided local extremum	Conclusion about sign of one-sided derivative	Quick explanation in terms of the difference quotient ${\frac {f(x)-f(c)}{x-c}}$	Prototypical pictures
1	Local maximum from the left implies left-hand derivative is nonnegative if it exists (has full proof + video)	$f$ has a (possibly, but not necessarily, strict) local maximum from the left at $c$.	The left-hand derivative $f'_{-}(c)$, if it exists, is positive or zero	In the difference quotient, the numerator is negative or zero and the denominator is negative. The quotient is thus positive or zero. Hence, so is the limit, if it exists.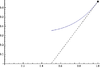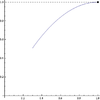
2	Local minimum from the left implies left-hand derivative is nonpositive if it exists	$f$ has a (possibly, but not necessarily, strict) local minimum from the left at $c$.	The left-hand derivative $f'_{-}(c)$, if it exists, is negative or zero	In the difference quotient, the numerator is positive or zero and the denominator is negative. The quotient is thus negative or zero. Hence, so is the limit, if it exists.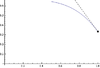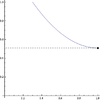
3	Local maximum from the right implies right-hand derivative is nonpositive if it exists	$f$ has a (possibly, but not necessarily, strict) local maximum from the right at $c$.	The right-hand derivative $f'_{+}(c)$, if it exists, is negative or zero	In the difference quotient, the numerator is negative or zero and the denominator is positive. The quotient is thus negative or zero. Hence, so is the limit, if it exists.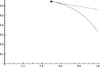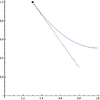
4	Local minimum from the right implies right-hand derivative is nonnegative if it exists	$f$ has a (possibly, but not necessarily, strict) local minimum from the right at $c$.	The right-hand derivative $f'_{+}(c)$, if it exists, is positive or zero	In the difference quotient, the numerator is positive or zero and the denominator is positive. The quotient is thus positive or zero. Hence, so is the limit, if it exists.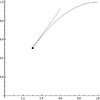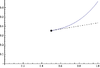

The video below provides an intuitive explanation of the above facts. For a full proof, see the page on Fact (1).

{{#widget:YouTube|id=sko6usPekeQ}}

Note on strictness

All the facts as stated above are for not necessarily strict one-sided local extrema, i.e., we allow $f(x)=f(c)$ for $x$ on the immediate left or right of $c$. However, even if we impose the additional condition of strictness, we still cannot eliminate the possibility of the one-sided derivative being zero. The reason is that even though the difference quotient must now be strictly positive or strictly negative in the various cases, the one-sided derivative, which is defined as a one-sided limit of the difference quotient, may still be equal to zero. All the prototypical pictures in the previous section are pictures of strict local extrema, and some of them show a one-sided derivative of zero.

For more, see the note on strictness in the proof for Fact (1).

This observation will be crucial when we piece together the two-sided information.

Note on sign sensitivity

In the facts used above, we see that, when ascertaining the sign of the difference quotient ${\frac {f(x)-f(c)}{x-c}}$, the following are true:

• The sign of the numerator is governed by whether the point is a point of local maximum or minimum. For a point of local maximum, the numerator is negative or zero, and for a point of local minimum, the numerator is positive or zero.
• The sign of the denominator is governed by whether we are approaching from the left or the right. For a left-sided approach, the denominator is negative and for a right-sided approach, the denominator is positive.

The upshot of this is that if we change the direction of approach while preserving the nature of the local extreme value, the sign of the one-sided derivative flips. This is crucial to the proof.

Proof

Proof idea

The idea is to convert two-sided local extremum information into both its one-sided pieces, then determine the signs of the one-sided derivatives. As noted in #Note on sign sensitivity, the sign conclusions for the two one-sided derivatives are opposite. We then pit these two pieces of information against each other to force the two-sided derivative, if it exists, to equal zero.

Local maximum case

Given: A function $f$, a point $c$ in the interior of the domain of $f$ such that $f$ attains a local maximum at $c$, i.e., $f(x)\leq f(c)$ for all $x\in (c-\delta ,c+\delta )$ for some choice of $\delta >0$.

To prove: If $\!f'(c)$ exists, then $\!f'(c)=0$

Proof

Step no.	Assertion/construction	Facts used	Given data used	Previous steps used	Explanation
1	If the left-hand derivative of $f$ at $c$ exists, then it is nonnegative, i.e., it is positive or zero.	Fact (1)	$f$ attains a (two-sided) local maximum at $c$		Since $f$ attains a two-sided local maximum at $c$, it in particular attains a local maximum from the left. Thus, Fact (1) applies.
2	If the right-hand derivative of $f$ at $c$ exists, then it is nonpositive, i.e., it is negative or zero.	Fact (3)	$f$ attains a (two-sided) local maximum at $c$		Since $f$ attains a two-sided local maximum at $c$, it in particular attains a local maximum from the right. Thus, Fact (3) applies.
3	If the (two-sided) derivative of $f$ exists at $c$, it must be zero.			Steps (1), (2)	For the (two-sided) derivative to exist, both the left-hand derivative and the right-hand derivative must exist and they must be equal to each other and to the derivative. By Step (1), the derivative must be positive or zero. By Step (2), the derivative must be negative or zero. The only way both of these can be simultaneously true is if the derivative equals zero.

{{#widget:YouTube|id=gExgdK8xKUs}}

Local minimum case

Given: A function $f$, a point $c$ in the interior of the domain of $f$ such that $f$ attains a local minimum at $c$, i.e., $f(x)\geq f(c)$ for all $x\in (c-\delta ,c+\delta )$ for some choice of $\delta >0$.

To prove: If $f'(c)$ exists, then $f'(c)=0$

Proof

Step no.	Assertion/construction	Facts used	Given data used	Previous steps used	Explanation
1	If the left-hand derivative of $f$ at $c$ exists, then it is nonpositive, i.e., it is negative or zero.	Fact (2)	$f$ attains a (two-sided) local minimum at $c$		Since $f$ attains a two-sided local minimum at $c$, it in particular attains a local minimum from the left. Thus, Fact (2) applies.
2	If the right-hand derivative of $f$ at $c$ exists, then it is nonnegative, i.e., it is positive or zero.	Fact (4)	$f$ attains a (two-sided) local minimum at $c$		Since $f$ attains a two-sided local minimum at $c$, it in particular attains a local minimum from the right. Thus, Fact (4) applies.
3	If the (two-sided) derivative of $f$ exists at $c$, it must be zero.			Steps (1), (2)	For the (two-sided) derivative to exist, both the left-hand derivative and the right-hand derivative must exist and they must be equal to each other and to the derivative. By Step (1), the derivative must be negative or zero. By Step (2), the derivative must be positive or zero. The only way both of these can be simultaneously true is if the derivative equals zero.

Note on strictness

Even if we consider the case of strict two-sided local maximum or strict two-sided local minimum, we can still have either of the two types of critical point: $f'(c)=0$ or $f'(c)$ not existing. The $f'(c)=0$ case continues to be possible because, for the one-sided versions, we can have the one-sided derivative equal to zero even assuming strict one-sided local extremum.