|
|
| (80 intermediate revisions by the same user not shown) |
| Line 1: |
Line 1: |
| {{perspectives}} | | {{perspectives}} |
| | | {{core term}} |
| ==Motivation== | | ==Motivation== |
|
| |
|
| Line 27: |
Line 27: |
|
| |
|
| This interpretation is sometimes termed the "two finger test" where one finger is used to follow the graph for <math>x</math> slightly less than <math>c</math> and the other finger is used to follow the graph for <math>x</math> slightly greater than <math>c</math>. | | This interpretation is sometimes termed the "two finger test" where one finger is used to follow the graph for <math>x</math> slightly less than <math>c</math> and the other finger is used to follow the graph for <math>x</math> slightly greater than <math>c</math>. |
| | |
| | The interpretation is problematic in that it is not really a definition, and fails to have computational utility for wildly oscillatory functions or functions with other forms of weird behavior. |
|
| |
|
| ===Two key ideas=== | | ===Two key ideas=== |
| Line 46: |
Line 48: |
|
| |
|
| 0:00:24.619,0:00:28.099 | | 0:00:24.619,0:00:28.099 |
| epsilon-delta definition. That was just an intuitive idea, | | epsilon-delta definition. This is just an intuitive idea, |
| and a few somewhat | | and a few somewhat |
|
| |
|
| Line 81: |
Line 83: |
| 0:01:02.050,0:01:06.640 | | 0:01:02.050,0:01:06.640 |
| number c, f(x) approaches some number L, and | | number c, f(x) approaches some number L, and |
| thatâs what this is:
| | that's what this is: |
|
| |
|
| 0:01:06.640,0:01:09.030 | | 0:01:06.640,0:01:09.030 |
| Line 92: |
Line 94: |
| 0:01:15.259,0:01:22.259 | | 0:01:15.259,0:01:22.259 |
| closer and closer to c, f(x) is sort of hanging | | closer and closer to c, f(x) is sort of hanging |
| around L. Itâs coming | | around L. It's coming |
|
| |
|
| 0:01:22.410,0:01:28.720 | | 0:01:22.410,0:01:28.720 |
| Line 100: |
Line 102: |
| 0:01:28.720,0:01:32.429 | | 0:01:28.720,0:01:32.429 |
| word limit is used in the English language: | | word limit is used in the English language: |
| One meaning its limit in | | One meaning is limit in |
|
| |
|
| 0:01:32.429,0:01:36.310 | | 0:01:32.429,0:01:36.310 |
| Line 111: |
Line 113: |
|
| |
|
| 0:01:41.319,0:01:46.220 | | 0:01:41.319,0:01:46.220 |
| language, which is limit as a boundary or | | language, which is limit as a boundary or as a cap or as a bound. |
| a as a gap or as a bound.
| |
|
| |
|
| 0:01:46.220,0:01:53.160 | | 0:01:46.220,0:01:53.160 |
| Line 119: |
Line 120: |
|
| |
|
| 0:01:53.160,0:01:58.640 | | 0:01:53.160,0:01:58.640 |
| food vault or something, and that sense of
| | fruit bowl or something, and that sense of |
| limit is not used ... for | | limit is not used ... for |
|
| |
|
| Line 135: |
Line 136: |
|
| |
|
| 0:02:11.800,0:02:18.800 | | 0:02:11.800,0:02:18.800 |
| so we donât get confused in mathematics. | | so we don't get confused in mathematics. |
| As I said, the idea is that | | As I said, the idea is that |
|
| |
|
| Line 151: |
Line 152: |
|
| |
|
| 0:02:32.740,0:02:37.980 | | 0:02:32.740,0:02:37.980 |
| smaller and smaller. This doesnât quite | | smaller and smaller. This doesn't quite |
| work unless your function is | | work unless your function is |
|
| |
|
| Line 163: |
Line 164: |
|
| |
|
| 0:02:46.750,0:02:52.170 | | 0:02:46.750,0:02:52.170 |
| doesnât really ⦠it's not very clear what
| | doesn't really ... it's not very clear what |
| we mean here without further | | we mean here without further |
|
| |
|
| Line 179: |
Line 180: |
| 0:03:09.180,0:03:13.430 | | 0:03:09.180,0:03:13.430 |
| which you may have seen in school. (well, | | which you may have seen in school. (well, |
| if youâve seen limits in | | if you've seen limits in |
|
| |
|
| 0:03:13.430,0:03:17.110 | | 0:03:13.430,0:03:17.110 |
| Line 197: |
Line 198: |
|
| |
|
| 0:03:35.990,0:03:42.990 | | 0:03:35.990,0:03:42.990 |
| This is x of c, so this is the value x of | | This is x is c, so this is the value x is |
| c, and this is a graph of | | c, and this is the graph of |
|
| |
|
| 0:03:44.069,0:03:48.310 | | 0:03:44.069,0:03:48.310 |
| Line 228: |
Line 229: |
|
| |
|
| 0:04:17.819,0:04:23.259 | | 0:04:17.819,0:04:23.259 |
| values ⦠so the function, the graph of it, | | values ... so the function, the graph of it, |
| the function values are | | the function values are |
|
| |
|
| 0:04:23.259,0:04:27.449 | | 0:04:23.259,0:04:27.449 |
| their prospective Y coordinates, so this is | | their respective y coordinates, so this is |
| x, this is Y, this is the | | x, this is y, this is the |
|
| |
|
| 0:04:27.449,0:04:34.449 | | 0:04:27.449,0:04:34.449 |
| graph. Y is f(x). When x is to the initial | | graph. y is f(x). When x is to the immediate |
| left of c, the value, Y | | left of c, the value, y |
|
| |
|
| 0:04:35.749,0:04:42.749 | | 0:04:35.749,0:04:42.749 |
| value, the Y approach f(x) value is ⦠are | | value, the y equals f(x) value is ... are |
| these values, so this or | | these values, so this or |
|
| |
|
| 0:04:44.610,0:04:51.610 | | 0:04:44.610,0:04:51.610 |
| this. As x approaches c from the left, the | | this. As x approaches c from the left, the |
| Y values are approaching
| | y values are approaching |
|
| |
|
| 0:04:53.699,0:04:57.240 | | 0:04:53.699,0:04:57.240 |
| the Y coordinate of this open circle. | | the y coordinate of this open circle. |
|
| |
|
| 0:04:57.240,0:05:04.240 | | 0:04:57.240,0:05:04.240 |
| Line 256: |
Line 257: |
| 0:05:05.680,0:05:10.830 | | 0:05:05.680,0:05:10.830 |
| approaching c from the left, then the limit | | approaching c from the left, then the limit |
| would be the Y coordinate | | would be the y coordinate |
|
| |
|
| 0:05:10.830,0:05:16.279 | | 0:05:10.830,0:05:16.279 |
| Line 263: |
Line 264: |
|
| |
|
| 0:05:16.279,0:05:22.749 | | 0:05:16.279,0:05:22.749 |
| right, so approaches from here ⦠the Y coordinate | | right, so approaches from here ... the y coordinate |
| is approaching the Y | | is approaching the y |
|
| |
|
| 0:05:22.749,0:05:29.749 | | 0:05:22.749,0:05:29.749 |
| Line 284: |
Line 285: |
|
| |
|
| 0:05:58.089,0:06:05.089 | | 0:05:58.089,0:06:05.089 |
| right, thatâs plus of f(x), | | right, that's plus of f(x), |
| is L2, and the value f of c is some third | | is L2, and the value f of c is some third |
|
| |
|
| 0:06:08.059,0:06:15.059 | | 0:06:08.059,0:06:15.059 |
| number. We donât know what | | number. We don't know what |
| it is, but f of c, L1, L2, are in this case | | it is, but f of c, L1, L2, are in this case |
|
| |
|
| Line 300: |
Line 301: |
| 0:06:25.900,0:06:28.259 | | 0:06:25.900,0:06:28.259 |
| concept of limit is usually a concept of two | | concept of limit is usually a concept of two |
| sides of limit, which
| | sided limit, which |
|
| |
|
| 0:06:28.259,0:06:33.419 | | 0:06:28.259,0:06:33.419 |
| Line 315: |
Line 316: |
|
| |
|
| 0:06:39.860,0:06:43.279 | | 0:06:39.860,0:06:43.279 |
| doesnât matter, so whether the value exists,
| | doesn't matter, so whether the value exists, |
| what it is, does not | | what it is, does not |
|
| |
|
| Line 335: |
Line 336: |
|
| |
|
| 0:07:03.499,0:07:07.749 | | 0:07:03.499,0:07:07.749 |
| sort of that. For the left-hand limit, you | | sort of that: for the left-hand limit, you |
| basically sort of follow | | basically sort of follow |
|
| |
|
| Line 343: |
Line 344: |
|
| |
|
| 0:07:11.499,0:07:15.789 | | 0:07:11.499,0:07:15.789 |
| get the Y coordinate of that. For the right-hand | | get the y coordinate of that. For the right-hand |
| limit, you follow | | limit, you follow |
|
| |
|
| 0:07:15.789,0:07:21.129 | | 0:07:15.789,0:07:21.129 |
| the graph on the right and see where they're | | the graph on the right and see where we're |
| headed to, and add the Y | | headed to, and get the y |
|
| |
|
| 0:07:21.129,0:07:22.240 | | 0:07:21.129,0:07:22.240 |
| Line 366: |
Line 367: |
|
| |
|
| 0:07:52.610,0:07:55.889 | | 0:07:52.610,0:07:55.889 |
| values are different. You could also have
| | value is different. You could also have |
| a situation where the value | | a situation where the value |
|
| |
|
| 0:07:55.889,0:08:00.460 | | 0:07:55.889,0:08:00.460 |
| doesnât exist at all. The function isn't
| | doesn't exist at all. The function isn't |
| defined at the point, but | | defined at the point, but |
|
| |
|
| 0:08:00.460,0:08:03.139 | | 0:08:00.460,0:08:03.139 |
| the limits still exist because the left-hand | | the limit still exists because the left-hand |
| limit and right-hand | | limit and right-hand |
|
| |
|
| Line 381: |
Line 382: |
|
| |
|
| 0:08:04.719,0:08:09.979 | | 0:08:04.719,0:08:09.979 |
| Now, all these examples, they're sort of a | | Now, all these examples, there's sort of a |
| crude way of putting this | | crude way of putting this |
|
| |
|
| Line 397: |
Line 398: |
|
| |
|
| 0:08:23.929,0:08:28.259 | | 0:08:23.929,0:08:28.259 |
| thatâs headed to, and use another finger
| | that's headed to, and use another finger |
| to trace the curve on the | | to trace the curve on the |
|
| |
|
| 0:08:28.259,0:08:33.640 | | 0:08:28.259,0:08:33.640 |
| immediate right and see where thatâs headed | | immediate right and see where that's headed |
| to, and if your two | | to, and if your two |
|
| |
|
| 0:08:33.640,0:08:38.270 | | 0:08:33.640,0:08:38.270 |
| fingers can meet each other, then the place | | fingers can meet each other, then the place |
| where they meet, the Y | | where they meet, the y |
|
| |
|
| 0:08:38.270,0:08:41.870 | | 0:08:38.270,0:08:41.870 |
| Line 417: |
Line 418: |
|
| |
|
| 0:08:46.940,0:08:51.120 | | 0:08:46.940,0:08:51.120 |
| is here, and then the limit doesnât exist | | is here, and then the limit doesn't exist |
| because the left-hand limit | | because the left-hand limit |
|
| |
|
| Line 425: |
Line 426: |
| 0:08:53.509,0:08:59.819 | | 0:08:53.509,0:08:59.819 |
| This, hopefully, you have seen in great detail | | This, hopefully, you have seen in great detail |
| where youâve done
| | when you've done |
|
| |
|
| 0:08:59.819,0:09:05.779 | | 0:08:59.819,0:09:05.779 |
| Line 433: |
Line 434: |
| 0:09:05.779,0:09:11.850 | | 0:09:05.779,0:09:11.850 |
| this two-finger test is not really a good | | this two-finger test is not really a good |
| definition of limit. Whatâs | | definition of limit. What's |
|
| |
|
| 0:09:11.850,0:09:13.600 | | 0:09:11.850,0:09:13.600 |
| Line 448: |
Line 449: |
|
| |
|
| 0:09:25.220,0:09:29.440 | | 0:09:25.220,0:09:29.440 |
| hard, and it doesnât really solve any problem. | | hard, and it doesn't really solve any problem. |
| It's not really a | | It's not really a |
|
| |
|
| Line 472: |
Line 473: |
| 0:09:50.040,0:09:56.990 | | 0:09:50.040,0:09:56.990 |
| things could give us trouble? Why do we need | | things could give us trouble? Why do we need |
| to define our | | to refine our |
|
| |
|
| 0:09:56.990,0:10:03.209 | | 0:09:56.990,0:10:03.209 |
| Line 486: |
Line 487: |
|
| |
|
| 0:10:18.220,0:10:21.899 | | 0:10:18.220,0:10:21.899 |
| have to develop a pure cut concept of limit | | have to develop a clear cut concept of limit |
| to be able to answer this | | to be able to answer this |
|
| |
|
| Line 498: |
Line 499: |
|
| |
|
| 0:10:32.920,0:10:39.920 | | 0:10:32.920,0:10:39.920 |
| just equal secant x. It's not that. It's sine | | just equal cosecant x. It's not that. It's sine |
| of 1 over x, and this | | of 1 over x, and this |
|
| |
|
| Line 506: |
Line 507: |
|
| |
|
| 0:10:50.220,0:10:52.660 | | 0:10:50.220,0:10:52.660 |
| that thatâs not defined, isn't good enough | | that that's not defined, isn't good enough |
| for us to say the limit | | for us to say the limit |
|
| |
|
| 0:10:52.660,0:10:55.139 | | 0:10:52.660,0:10:55.139 |
| doesn't [inaudible 00:10:36] we actually have | | doesn't exist; we actually have |
| to try to make a picture | | to try to make a picture |
|
| |
|
| 0:10:55.139,0:10:57.660 | | 0:10:55.139,0:10:57.660 |
| of this and try to understand what the limit | | of this and try to understand what the limit |
| is here. | | is going to be. |
|
| |
|
| 0:10:57.660,0:11:04.660 | | 0:10:57.660,0:11:04.660 |
| Line 522: |
Line 523: |
|
| |
|
| 0:11:12.560,0:11:19.560 | | 0:11:12.560,0:11:19.560 |
| will sine 1 over x look? Let's start of where | | will sine 1 over x look? Let's start off where |
| x is nearly infinity. | | x is nearly infinity. |
|
| |
|
| Line 535: |
Line 536: |
| 0:11:30.660,0:11:36.879 | | 0:11:30.660,0:11:36.879 |
| therefore slightly positive. It's like here. | | therefore slightly positive. It's like here. |
| It's going to start up | | It's going to start off |
|
| |
|
| 0:11:36.879,0:11:42.810 | | 0:11:36.879,0:11:42.810 |
| with an S [inaudible 00:11:21] at zero. Then | | with an asymptote, a horizontal asymptote, at zero. |
| it's going to sort of go | | Then it's going to sort of go |
|
| |
|
| 0:11:42.810,0:11:49.420 | | 0:11:42.810,0:11:49.420 |
| Line 565: |
Line 566: |
|
| |
|
| 0:12:16.990,0:12:21.160 | | 0:12:16.990,0:12:21.160 |
| 1 over 3 pi, and so on. Whatâs going to | | 1 over 3 pi, and so on. What's going to |
| happen is that near zero it's | | happen is that near zero it's |
|
| |
|
| Line 605: |
Line 606: |
|
| |
|
| 0:13:38.850,0:13:45.060 | | 0:13:38.850,0:13:45.060 |
| Iâm not being very accurate here, but just
| | I'm not being very accurate here, but just |
| the idea. The pen or | | the idea. The pen or |
|
| |
|
| Line 629: |
Line 630: |
|
| |
|
| 0:14:18.050,0:14:21.579 | | 0:14:18.050,0:14:21.579 |
| this, this ⦠you're sort of getting close | | this, this ... you're sort of getting close |
| to here but still not quite | | to zero but still not quite |
|
| |
|
| 0:14:21.579,0:14:28.579 | | 0:14:21.579,0:14:28.579 |
| reaching it. It's ⦠where are you headed? | | reaching it. It's ... where are you headed? |
| It's kind of a little | | It's kind of a little |
|
| |
|
| 0:14:31.610,0:14:36.879 | | 0:14:31.610,0:14:36.879 |
| unclear. Notice, it's not that just because | | unclear. Notice, it's not that just because |
| we plug in zero doesnât | | we plug in zero doesn't |
|
| |
|
| 0:14:36.879,0:14:39.170 | | 0:14:36.879,0:14:39.170 |
| make sense, the limit doesn't... Thatâs | | make sense, the limit doesn't... That's |
| not the issue. The issue is | | not the issue. The issue is |
|
| |
|
| 0:14:39.170,0:14:43.249 | | 0:14:39.170,0:14:43.249 |
| that after you make the graph, it's unclear | | that after you make the graph, it's unclear |
| whatâs happening.
| | what's happening. |
|
| |
|
| 0:14:43.249,0:14:49.329 | | 0:14:43.249,0:14:49.329 |
| One kind of logic is that the other limit | | One kind of logic is that, yeah, the limit |
| is zero? Why? Well, it's | | is zero? Why? Well, it's |
|
| |
|
| 0:14:49.329,0:14:52.949 | | 0:14:49.329,0:14:52.949 |
| kind of balance around here. It's a bit above | | kind of balanced around zero, right? It's a bit |
| and below, and it keeps | | above and below, and it keeps |
|
| |
|
| 0:14:52.949,0:14:59.949 | | 0:14:52.949,0:14:59.949 |
| Line 669: |
Line 670: |
|
| |
|
| 0:15:12.459,0:15:17.449 | | 0:15:12.459,0:15:17.449 |
| If you think of limit as something thatâs | | If you think of limit as something it's |
| approaching, then as x | | approaching, then as x |
|
| |
|
| Line 681: |
Line 682: |
|
| |
|
| 0:15:36.550,0:15:41.920 | | 0:15:36.550,0:15:41.920 |
| zero, any small ⦠this you make around zero, | | zero, any small ... this you make around zero, |
| the graph is going to | | the graph is going to |
|
| |
|
| Line 692: |
Line 693: |
|
| |
|
| 0:15:47.269,0:15:50.300 | | 0:15:47.269,0:15:50.300 |
| oscillating with the minus 1 and 1. However, | | oscillating within [-1,1]. However |
| smaller interval you
| | small an interval you |
|
| |
|
| 0:15:50.300,0:15:54.540 | | 0:15:50.300,0:15:54.540 |
| Line 728: |
Line 729: |
|
| |
|
| 0:16:28.639,0:16:33.089 | | 0:16:28.639,0:16:33.089 |
| close and stay close. So thatâs actually | | close and stay close. So that's actually |
| key idea number two we have | | key idea number two we have |
|
| |
|
| 0:16:33.089,0:16:38.290 | | 0:16:33.089,0:16:38.290 |
| here the function ⦠for the function to | | here the function ... for the function to |
| have a limit at the point, the | | have a limit at the point, the |
|
| |
|
| Line 743: |
Line 744: |
|
| |
|
| 0:16:45.079,0:16:49.459 | | 0:16:45.079,0:16:49.459 |
| This is, therefore, it doesnât have a limit | | This is, therefore, it doesn't have a limit |
| at zero because the | | at zero because the |
|
| |
|
| Line 751: |
Line 752: |
|
| |
|
| 0:16:54.420,0:17:01.059 | | 0:16:54.420,0:17:01.059 |
| trap the function values. You cannot say that⦠| | trap the function values. You cannot say that... |
| you cannot trap the | | you cannot trap the |
|
| |
|
| Line 782: |
Line 783: |
|
| |
|
| 0:17:30.330,0:17:33.890 | | 0:17:30.330,0:17:33.890 |
| need to remember is that the function doesnât | | need to remember is that the function doesn't |
| just need to come close | | just need to come close |
|
| |
|
| Line 821: |
Line 822: |
|
| |
|
| 0:18:30.550,0:18:37.550 | | 0:18:30.550,0:18:37.550 |
| of ⦠whatâs close enough? Is 2.1 close | | of ... what's close enough? Is 2.1 close |
| enough? No, thatâs too far. | | enough? No, that's too far. |
|
| |
|
| 0:18:38.750,0:18:43.380 | | 0:18:38.750,0:18:43.380 |
| Line 828: |
Line 829: |
|
| |
|
| 0:18:43.380,0:18:47.420 | | 0:18:43.380,0:18:47.420 |
| Now, if you werenât a mathematician, you | | Now, if you weren't a mathematician, you |
| would probably say, "Yes, | | would probably say, "Yes, |
|
| |
|
| Line 876: |
Line 877: |
| 0:19:59.990,0:20:05.940 | | 0:19:59.990,0:20:05.940 |
| this picture, and I change it to, let's say | | this picture, and I change it to, let's say |
| ⦠so I replace this
| | ... so I replace this |
|
| |
|
| 0:20:05.940,0:20:11.410 | | 0:20:05.940,0:20:11.410 |
| Line 902: |
Line 903: |
|
| |
|
| 0:20:32.040,0:20:35.000 | | 0:20:32.040,0:20:35.000 |
| behavior sort of at this time that point or | | behavior, sort of at that point or |
| farther away than that | | farther away than that |
|
| |
|
| 0:20:35.000,0:20:42.000 | | 0:20:35.000,0:20:42.000 |
| point, then the behavior close to 2 doesnât | | point, then the behavior close to 2 doesn't |
| get affected. Thatâs the | | get affected. That's the |
|
| |
|
| 0:20:42.820,0:20:46.660 | | 0:20:42.820,0:20:46.660 |
| other key idea here. Actually I did these | | other key idea here. Actually I did these |
| in [inaudible 00:20:30]. | | in reverse order. |
|
| |
|
| 0:20:46.660,0:20:52.060 | | 0:20:46.660,0:20:52.060 |
| Thatâs how it is coming, actually, but I'll
| | That's how it was coming naturally, but I'll |
| just say it again. | | just say it again. |
|
| |
|
| Line 922: |
Line 923: |
|
| |
|
| 0:20:56.570,0:21:00.210 | | 0:20:56.570,0:21:00.210 |
| doesnât depend on the behavior at any single
| | doesn't depend on the behavior at any single |
| specific other point. It | | specific other point. It |
|
| |
|
| Line 942: |
Line 943: |
|
| |
|
| 0:21:19.790,0:21:26.790 | | 0:21:19.790,0:21:26.790 |
| tracked near the point for the limit notion
| | trapped near the point for the limit notion |
| to be true. This type of | | to be true. This type of |
|
| |
|
| Line 958: |
Line 959: |
|
| |
|
| 0:21:40.590,0:21:47.590 | | 0:21:40.590,0:21:47.590 |
| strip. In that case, the limit doesnât exist. | | strip. In that case, the limit doesn't exist. |
| In subsequent videos, | | In subsequent videos, |
|
| |
|
| 0:21:48.550,0:21:54.630 | | 0:21:48.550,0:21:54.630 |
| we'll see Epsilon definition, we'll do a bit | | we'll see the epsilon delta definition, we'll do a bit |
| of formalism to that, and | | of formalism to that, and |
|
| |
|
| Line 972: |
Line 973: |
| understanding.</toggledisplay> | | understanding.</toggledisplay> |
|
| |
|
| | '''Checkpoint questions''': |
| | |
| | * To figure out the limit of a function at <math>2</math>, does the value of the function at <math>2.1</math> matter? Does the value of the function at <math>2.01</math> matter? <math>2.001</math>? How close is close enough? |
| | * What is the limit <math>\lim_{x \to 0} \sin(1/x)</math>? What's the intuitive idea behind the reasoning? More formal versions of this reasoning will be introduced after we have seen the <math>\varepsilon-\delta</math> definition. |
|
| |
|
| ==Definition for finite limit for function of one variable== | | ==Definition for finite limit for function of one variable== |
| Line 983: |
Line 988: |
| <math>\lim_{x \to c} f(x) = L</math> | | <math>\lim_{x \to c} f(x) = L</math> |
|
| |
|
| if the following holds (the single sentence is broken down into multiple points to make it clearer): | | if the following holds: |
| | |
| | {{quotation|For every <math>\varepsilon > 0</math>, there exists <math>\delta > 0</math> such that for all <math>x \in \R</math> satisfying <math>0 < |x - c| < \delta</math>, we have <math>|f(x) - L| < \varepsilon</math>.}} |
|
| |
|
| * For every <math>\varepsilon > 0</math> (the symbol <math>\varepsilon</math> is a Greek lowercase letter pronounced "epsilon")
| | The definition is broken down into its four clauses below: |
| * there exists <math>\delta > 0</math> such that (the symbol <math>\delta</math> is a Greek lowercase letter pronounced "delta")
| | |
| * for all <math>x \in \R</math> satisfying <math>0 < |x - c| < \delta</math> (explicitly, <math>x \in (c - \delta,c) \cup (c, c+ \delta) = (c - \delta, c + \delta) \setminus \{ c \}</math>),
| | {| class="sortable" border="1" |
| * we have <math>|f(x) - L| < \varepsilon</math> (explicitly, <math>f(x) \in (L - \varepsilon,L + \varepsilon)</math>).
| | ! Clause !! Interval description !! Symbol explanations |
| | |- |
| | | For every <math>\varepsilon > 0</math> || <math>\varepsilon \in (0,\infty)</math> || The symbol <math>\varepsilon</math> is a Greek lowercase letter pronounced "epsilon".<br>Although the definition customarily uses the letter <math>\varepsilon</math>, it can be replaced by any other letter, as long as the letter is different from the other letters in use. The reason for sticking to a standard letter choice is that it reduces cognitive overload. |
| | |- |
| | | there exists <math>\delta > 0</math> such that || <math>\delta \in (0,\infty)</math> || The symbol <math>\delta</math> is a Greek lowercase letter pronounced "delta"<br>Although the definition customarily uses the letter <math>\varepsilon</math>, it can be replaced by any other letter, as long as the letter is different from the other letters in use. The reason for sticking to a standard letter choice is that it reduces cognitive overload. |
| | |- |
| | | for all <math>x \in \R</math> satisfying <math>0 < |x - c| < \delta</math> || <math>x \in (c - \delta,c) \cup (c, c+ \delta) = (c - \delta, c + \delta) \setminus \{ c \}</math> || The symbol <math>| \ \ |</math> stands for the [[absolute value function]].<br><math>\in</math> stands for "is in the set" so the statements should be read as saying that <math>x</math> is in the set described in the two equivalent ways.<br><math>\cup</math> stands for the union, so the statement that <math>x \in (c - \delta,c) \cup (c, c+ \delta)</math> should be parsed as saying that <math>x \in (c - \delta,c)</math> ''or'' <math>x \in (c, c + \delta)</math><br><math>\setminus</math> stands for set difference, so the statement <math>x \in (c - \delta, c + \delta) \setminus \{ c \}</math> can be parsed as saying that <math>x</math> could be any value in <math>(c - \delta, c + \delta)</math> '''except''' <math>c</math>. The point <math>c</math> is excluded because we do not want the value of <math>f</math> at <math>c</math> to affect the limit notion. |
| | |- |
| | | we have <math>|f(x) - L| < \varepsilon</math> || <math>f(x) \in (L - \varepsilon,L + \varepsilon)</math> || The symbol <math>| \ \ |</math> stands for the [[absolute value function]].<br><math>\in</math> stands for "is in the set" so the statement should be read as saying that <math>f(x)</math> is in the set <math>(L - \varepsilon, L + \varepsilon)</math>. |
| | |} |
|
| |
|
| The '''limit''' (also called the '''two-sided limit''') <math>\lim_{x \to c} f(x)</math> is defined as a value <math>L \in \R</math> such that <math>\lim_{x \to c} f(x) = L</math>. By the [[uniqueness theorem for limits]], there is at most one value of <math>L \in \R</math> for which <math>\lim_{x \to c} f(x) = L</math>. Hence, it makes sense to talk of ''the'' limit when it exists. | | The '''limit''' (also called the '''two-sided limit''') <math>\lim_{x \to c} f(x)</math> is defined as a value <math>L \in \R</math> such that <math>\lim_{x \to c} f(x) = L</math>. By the [[uniqueness theorem for limits]], there is at most one value of <math>L \in \R</math> for which <math>\lim_{x \to c} f(x) = L</math>. Hence, it makes sense to talk of ''the'' limit when it exists. |
| Line 1,192: |
Line 1,208: |
| L that's called the limit.</toggledisplay> | | L that's called the limit.</toggledisplay> |
|
| |
|
| ''Note'': Although the definition customarily uses the letters <math>\varepsilon</math> and <math>\delta</math>, any other letters can be used, as long as these letters are different from each other and from the letters already in use. The reason for sticking to a standard letter choice is that it reduces cognitive overload. | | '''Checkpoint questions''': |
| | |
| | * In order to make sense of <math>\lim_{x \to c} f(x) = L</math> where must the function <math>f</math> be defined? Must <math>f</math> be defined ''at'' <math>c</math>? If <math>f(c)</math> exists, what can we say about its value? |
| | * What's the formal definition of limit, i.e., what does <math>\lim_{x \to c} f(x) = L</math> mean? |
| | * How would you write the formal definition of limit using intervals rather than absolute value inequalities to describe where <math>x</math> and <math>f(x)</math> should be? |
| | * Why is there a "<math>0 < </math>" in the inequality <math>0 < |x - c| < \delta</math> in the <math>\varepsilon-\delta</math> definition? Why doesn't a <math>0 < </math> appear in the <math>|f(x) - L| < \varepsilon</math> part of the definition? |
| | * In order to be able to talk of ''the'' limit <math>\lim_{x \to c} f(x)</math>, what additional fact do we need beyond the definition of what <math>\lim_{x \to c} f(x) = L</math> means? |
|
| |
|
| ===Left hand limit=== | | ===Left-hand limit=== |
|
| |
|
| Suppose <math>f</math> is a [[function]] of one variable and <math>c \in \R</math> is a point such that <math>f</math> is defined on the immediate left of <math>c</math> (note that <math>f</math> may or may not be defined at <math>c</math>). In other words, there exists some value <math>t > 0</math> such that <math>f</math> is defined on <math>(c-t,c)</math>. | | Suppose <math>f</math> is a [[function]] of one variable and <math>c \in \R</math> is a point such that <math>f</math> is defined on the immediate left of <math>c</math> (note that <math>f</math> may or may not be defined at <math>c</math>). In other words, there exists some value <math>t > 0</math> such that <math>f</math> is defined on <math>(c-t,c)</math>. |
| Line 1,202: |
Line 1,224: |
| <math>\lim_{x \to c^-} f(x) = L</math> | | <math>\lim_{x \to c^-} f(x) = L</math> |
|
| |
|
| if the following holds (the single sentence is broken down into multiple points to make it clearer): | | if the following holds: |
| | |
| | {{quotation|For every <math>\varepsilon > 0</math>, there exists <math>\delta > 0</math> such that for all <math>x \in \R</math> satisfying <math>0 < c - x < \delta</math>, we have <math>|f(x) - L| < \varepsilon</math>.}} |
| | |
| | The definition is broken down into its four clauses below: |
|
| |
|
| * For every <math>\varepsilon > 0</math>
| | {| class="sortable" border="1" |
| * there exists <math>\delta > 0</math> such that
| | ! Clause !! Interval description !! Symbol explanations |
| * for all <math>x \in \R</math> satisfying <math>0 < c - x < \delta</math> (explicitly, <math>x \in (c - \delta,c)</math>),
| | |- |
| * we have <math>|f(x) - L| < \varepsilon</math> (explicitly, <math>f(x) \in (L - \varepsilon,L + \varepsilon)</math>.
| | | For every <math>\varepsilon > 0</math> || <math>\varepsilon \in (0,\infty)</math> || The symbol <math>\varepsilon</math> is a Greek lowercase letter pronounced "epsilon".<br>Although the definition customarily uses the letter <math>\varepsilon</math>, it can be replaced by any other letter, as long as the letter is different from the other letters in use. The reason for sticking to a standard letter choice is that it reduces cognitive overload. |
| | |- |
| | | there exists <math>\delta > 0</math> such that || <math>\delta \in (0,\infty)</math> || The symbol <math>\delta</math> is a Greek lowercase letter pronounced "delta"<br>Although the definition customarily uses the letter <math>\varepsilon</math>, it can be replaced by any other letter, as long as the letter is different from the other letters in use. The reason for sticking to a standard letter choice is that it reduces cognitive overload. |
| | |- |
| | | for all <math>x \in \R</math> satisfying <math>0 < c - x < \delta</math> || <math>x \in (c - \delta,c)</math> || The symbol <math>| \ \ |</math> stands for the [[absolute value function]].<br><math>\in</math> stands for "is in the set" so the statements should be read as saying that <math>x</math> is in the set <math>(c - \delta,c)</math> describing the immediate <math>\delta</math>-left of <math>c</math>. |
| | |- |
| | | we have <math>|f(x) - L| < \varepsilon</math> || <math>f(x) \in (L - \varepsilon,L + \varepsilon)</math> || The symbol <math>| \ \ |</math> stands for the [[absolute value function]].<br><math>\in</math> stands for "is in the set" so the statement should be read as saying that <math>f(x)</math> is in the set <math>(L - \varepsilon, L + \varepsilon)</math>. |
| | |} |
|
| |
|
| The '''left hand limit''' (acronym '''LHL''') <math>\lim_{x \to c^-} f(x)</math> is defined as a value <math>L \in \R</math> such that <math>\lim_{x \to c^-} f(x) = L</math>. By the [[uniqueness theorem for limits]] (one-sided version), there is at most one value of <math>L \in \R</math> for which <math>\lim_{x \to c^-} f(x) = L</math>. Hence, it makes sense to talk of ''the'' left hand limit when it exists. | | The '''left-hand limit''' (acronym '''LHL''') <math>\lim_{x \to c^-} f(x)</math> is defined as a value <math>L \in \R</math> such that <math>\lim_{x \to c^-} f(x) = L</math>. By the [[uniqueness theorem for limits]] (one-sided version), there is at most one value of <math>L \in \R</math> for which <math>\lim_{x \to c^-} f(x) = L</math>. Hence, it makes sense to talk of ''the'' left hand limit when it exists. |
|
| |
|
| ===Right hand limit=== | | ===Right-hand limit=== |
|
| |
|
| Suppose <math>f</math> is a [[function]] of one variable and <math>c \in \R</math> is a point such that <math>f</math> is defined on the immediate right of <math>c</math> (note that <math>f</math> may or may not be defined at <math>c</math>). In other words, there exists some value <math>t > 0</math> such that <math>f</math> is defined on <math>(c,c+t)</math>. | | Suppose <math>f</math> is a [[function]] of one variable and <math>c \in \R</math> is a point such that <math>f</math> is defined on the immediate right of <math>c</math> (note that <math>f</math> may or may not be defined at <math>c</math>). In other words, there exists some value <math>t > 0</math> such that <math>f</math> is defined on <math>(c,c+t)</math>. |
| Line 1,219: |
Line 1,252: |
| <math>\lim_{x \to c^+} f(x) = L</math> | | <math>\lim_{x \to c^+} f(x) = L</math> |
|
| |
|
| if the following holds (the single sentence is broken down into multiple points to make it clearer): | | if the following holds: |
| | |
| | {{quotation|For every <math>\varepsilon > 0</math>, there exists <math>\delta > 0</math> such that for all <math>x \in \R</math> satisfying <math>0 < x - c < \delta</math>, we have <math>|f(x) - L| < \varepsilon</math>.}} |
| | |
| | The definition is broken down into its four clauses below: |
|
| |
|
| * For every <math>\varepsilon > 0</math>
| | {| class="sortable" border="1" |
| * there exists <math>\delta > 0</math> such that
| | ! Clause !! Interval description !! Symbol explanations |
| * for all <math>x \in \R</math> satisfying <math>0 < x - c < \delta</math> (explicitly, <math>x \in (c,c + \delta)</math>),
| | |- |
| * we have <math>|f(x) - L| < \varepsilon</math> (explicitly, <math>f(x) \in (L - \varepsilon,L + \varepsilon)</math>.
| | | For every <math>\varepsilon > 0</math> || <math>\varepsilon \in (0,\infty)</math> || The symbol <math>\varepsilon</math> is a Greek lowercase letter pronounced "epsilon".<br>Although the definition customarily uses the letter <math>\varepsilon</math>, it can be replaced by any other letter, as long as the letter is different from the other letters in use. The reason for sticking to a standard letter choice is that it reduces cognitive overload. |
| | |- |
| | | there exists <math>\delta > 0</math> such that || <math>\delta \in (0,\infty)</math> || The symbol <math>\delta</math> is a Greek lowercase letter pronounced "delta"<br>Although the definition customarily uses the letter <math>\varepsilon</math>, it can be replaced by any other letter, as long as the letter is different from the other letters in use. The reason for sticking to a standard letter choice is that it reduces cognitive overload. |
| | |- |
| | | for all <math>x \in \R</math> satisfying <math>0 < x - c < \delta</math> || <math>x \in (c,c + \delta)</math> || The symbol <math>| \ \ |</math> stands for the [[absolute value function]].<br><math>\in</math> stands for "is in the set" so the statements should be read as saying that <math>x</math> is in the set <math>(c,c + \delta)</math> describing the immediate <math>\delta</math>-right of <math>c</math>. |
| | |- |
| | | we have <math>|f(x) - L| < \varepsilon</math> || <math>f(x) \in (L - \varepsilon,L + \varepsilon)</math> || The symbol <math>| \ \ |</math> stands for the [[absolute value function]].<br><math>\in</math> stands for "is in the set" so the statement should be read as saying that <math>f(x)</math> is in the set <math>(L - \varepsilon, L + \varepsilon)</math>. |
| | |} |
| | |
| | The '''right-hand limit''' (acronym '''RHL''') <math>\lim_{x \to c^+} f(x)</math> is defined as a value <math>L \in \R</math> such that <math>\lim_{x \to c^+} f(x) = L</math>. By the [[uniqueness theorem for limits]] (one-sided version), there is at most one value of <math>L \in \R</math> for which <math>\lim_{x \to c^+} f(x) = L</matH>. Hence, it makes sense to talk of ''the'' right hand limit when it exists. |
| | |
| | ===Side-by-side comparison of the definitions=== |
|
| |
|
| The '''right hand limit''' (acronym '''RHL''') <math>\lim_{x \to c^+} f(x)</math> is defined as a value <math>L \in \R</math> such that <math>\lim_{x \to c^+} f(x) = L</math>. By the [[uniqueness theorem for limits]] (one-sided version), there is at most one value of <math>L \in \R</math> for which <math>\lim_{x \to c^+} f(x) = L</matH>. Hence, it makes sense to talk of ''the'' right hand limit when it exists.
| | {| class="sortable" border="1" |
| | ! Clause for two-sided limit <math>\lim_{x \to c} f(x) = L</math> !! Clause for left hand limit <math>\lim_{x \to c^-} f(x) = L</math> !! Clause for right hand limit <math>\lim_{x \to c^+} f(x) = L</math>!! Comments |
| | |- |
| | | For every <math>\varepsilon > 0</math> || For every <math>\varepsilon > 0</math> || For every <math>\varepsilon > 0</math> || identical so far |
| | |- |
| | | there exists <math>\delta > 0</math> such that || there exists <math>\delta > 0</math> such that || there exists <math>\delta > 0</math> such that || still identical |
| | |- |
| | | for all <math>x \in \R</math> satisfying <math>0 < |x - c| < \delta</math>, i.e., <math>x \in (c - \delta,c) \cup (c,c + \delta)</math> || for all <math>x \in \R</math> satisfying <math>0 < c - x < \delta</math>, i.e., <math>x \in (c - \delta,c)</math> || for all <math>x \in \R</math> satisfying <math>0 < x - c < \delta</math>, i.e., <math>x \in (c,c + \delta)</math> || this is the part that differs, in so far as it is the direction of domain approach that differs between the definitions. |
| | |- |
| | | we have <math>|f(x) - L| < \varepsilon</math>, i.e., <math>f(x) \in (L - \varepsilon,L + \varepsilon)</math> || we have <math>|f(x) - L| < \varepsilon</math>, i.e., <math>f(x) \in (L - \varepsilon,L + \varepsilon)</math> || we have <math>|f(x) - L| < \varepsilon</math>, i.e., <math>f(x) \in (L - \varepsilon,L + \varepsilon)</math> || this part is again identical. Note that the left versus right is only about the direction of approach in the domain, not about the direction of approach of the function value. |
| | |} |
|
| |
|
| <center>{{#widget:YouTube|id=qBjqc78KGx0}}</center> | | <center>{{#widget:YouTube|id=qBjqc78KGx0}}</center> |
| Line 1,619: |
Line 1,677: |
| 0:11:07.000,0:11:09.000 | | 0:11:07.000,0:11:09.000 |
| Okay? [END!]</toggledisplay> | | Okay? [END!]</toggledisplay> |
| | |
| | '''Checkpoint questions''': |
| | |
| | * In order to make sense of <math>\lim_{x \to c^-} f(x) = L</math>, where must the function <math>f</math> be defined? Must <math>f</math> be defined ''at'' <math>c</math>? If <math>f(c)</math> exists, what can we say about its value? |
| | * The definitions of left hand limit, right hand limit and ordinary (two-sided) limit are pretty similar. There is only one clause that differs across the three definitions. What clause is this, and how does it differ across the definitions? Explain both in inequality notation and in interval notation. |
| | * Why should we be careful when dealing with one-sided limits in the context of function compositions? |
|
| |
|
| ===Relation between the limit notions=== | | ===Relation between the limit notions=== |
|
| |
|
| The two-sided limit exists if and only if (both the left hand limit and right hand limit exist and they are equal to each other). | | The two-sided limit exists if and only if (both the left hand limit and right hand limit exist) '''and''' (they are equal to each other). |
|
| |
|
| ==Definition of finite limit for function of one variable in terms of a game==
| | Explicitly, <math>\lim_{x \to c} f(x)</math> exists if '''all three''' of these conditions hold: |
|
| |
|
| The formal definitions of limit, as well as of one-sided limit, can be reframed in terms of a game. This is a special instance of an approach that turns any statement with existential and universal quantifiers into a game. | | * <math>\lim_{x \to c^-} f(x)</math> exists. |
| | * <math>\lim_{x \to c^+} f(x)</math> exists. |
| | * <math>\lim_{x \to c^-} f(x) = \lim_{x \to c^+} f(x)</math>. |
| | |
| | Moreover, in the event that both one-sided limits exist and are equal, the two-sided limit is equal to both of them. |
| | |
| | Further, a particular value of <math>\delta > 0</math> works for a particular value of <math>\varepsilon > 0</math> in the two-sided limit definition if and only if it works in both the left hand limit definition and the right hand limit definition. |
| | |
| | ==Definition of finite limit for function of one variable in terms of a game== |
| | |
| | The formal definitions of limit, as well as of one-sided limit, can be reframed in terms of a game. This is a special instance of an approach that turns any statement with existential and universal quantifiers into a game. |
|
| |
|
| ===Two-sided limit=== | | ===Two-sided limit=== |
| Line 1,634: |
Line 1,708: |
| <math>\!\lim_{x \to c} f(x) = L</math> | | <math>\!\lim_{x \to c} f(x) = L</math> |
|
| |
|
| Note that there is one trivial sense in which the above statement can be false, or rather, meaningless, namely, that <math>f</math> is not defined on the immediate left or immediate right of <math>c</math>. In that case, the limit statement above is false, but moreover, it is meaningless to even consider the notion of limit. | | Note that there is one trivial sense in which the above statement can be false, or rather, meaningless, namely, that <math>f</math> is not defined on the immediate left or immediate right of <math>c</math>. In that case, the limit statement above is false, but moreover, it is meaningless to even consider the notion of limit. We therefore omit this sense from consideration and consider instead only the situation where <math>f</math> is defined on the immediate left and immediate right of <math>c</math>. |
|
| |
|
| The game is between two players, a '''Prover''' whose goal is to prove that the limit statement is true, and a '''Skeptic''' (also called a '''Verifier''' or sometimes a '''Disprover''') whose goal is to show that the statement is false. The game has three moves: | | The game is between two players, a '''Prover''' whose goal is to prove that the limit statement is true, and a '''Skeptic''' (also called a '''Verifier''' or sometimes a '''Disprover''') whose goal is to show that the statement is false. The game has three moves: |
|
| |
|
| # First, the skeptic chooses <math>\varepsilon > 0</math>, or equivalently, chooses the target interval <math>(L - \varepsilon,L + \varepsilon)</math>. | | # First, the skeptic chooses <math>\varepsilon > 0</math>, or equivalently, chooses the target interval <math>(L - \varepsilon,L + \varepsilon)</math> in which the skeptic is challenging the prover to ''trap'' the function. |
| # Then, the prover chooses <math>\delta > 0</math>, or equivalently, chooses the interval <math>(c - \delta, c + \delta) \setminus \{ c \}</math>. | | # Then, the prover chooses <math>\delta > 0</math>, or equivalently, chooses the interval <math>(c - \delta, c + \delta) \setminus \{ c \}</math>. |
| # Then, the skeptic chooses a value <math>x</math> satisfying <math>0 < |x - c| < \delta</math>, or equivalently, <math>x \in (c - \delta, c + \delta) \setminus \{ c \}</math>, which is the same as <math>(c - \delta,c) \cup (c,c + \delta)</math>. | | # Then, the skeptic chooses a value <math>x</math> satisfying <math>0 < |x - c| < \delta</math>, or equivalently, <math>x \in (c - \delta, c + \delta) \setminus \{ c \}</math>, which is the same as <math>(c - \delta,c) \cup (c,c + \delta)</math>. |
|
| |
|
| Now, if <math>|f(x) - L| < \varepsilon</math> (i.e., <math>f(x) \in (L - \varepsilon,L + \varepsilon)</math>), the prover wins. Otherwise, the skeptic wins (see the subtlety about the domain of definition issue below the picture). | | Now, if <math>|f(x) - L| < \varepsilon</math> (i.e., <math>f(x) \in (L - \varepsilon,L + \varepsilon)</math>), the prover wins. Otherwise, the skeptic wins. |
|
| |
|
| We say that the limit statement | | We say that the limit statement |
| Line 1,648: |
Line 1,722: |
| <math>\!\lim_{x \to c} f(x) = L</math> | | <math>\!\lim_{x \to c} f(x) = L</math> |
|
| |
|
| is '''true''' if the prover has a winning strategy for this game. The ''winning strategy'' for the prover basically constitutes a strategy to choose an appropriate <math>\delta</math> in terms of the <matH>\varepsilon</math> chosen by the skeptic. Thus, it is an expression of <math>\delta</math> as a function of <math>\varepsilon</math>. | | is '''true''' if the prover has a '''winning strategy''' for this game. The ''winning strategy'' for the prover basically constitutes a strategy to choose an appropriate <math>\delta</math> in terms of the <math>\varepsilon</math> chosen by the skeptic. Thus, it is an expression of <math>\delta</math> as a function of <math>\varepsilon</math>. Verbally, the goal of the prover is to choose a value of <math>\delta</math> so that when the input is restricted to being within <math>\delta</math> distance of <math>c</math>, the output is '''trapped''' to within <math>\varepsilon</math> distance of the claimed limit <math>L</math>. |
|
| |
|
| We say that the limit statement | | We say that the limit statement |
| Line 1,655: |
Line 1,729: |
|
| |
|
| is '''false''' if the skeptic has a winning strategy for this game. The '''winning strategy''' for the skeptic involves a choice of <math>\varepsilon</math>, ''and'' a strategy that chooses a value of <math>x</math> (constrained in the specified interval) based on the prover's choice of <math>\delta</math>. | | is '''false''' if the skeptic has a winning strategy for this game. The '''winning strategy''' for the skeptic involves a choice of <math>\varepsilon</math>, ''and'' a strategy that chooses a value of <math>x</math> (constrained in the specified interval) based on the prover's choice of <math>\delta</math>. |
| | |
| | Let's review the definition in conjunction with the game along with a deeper semantic understanding of the steps: |
| | |
| | {| class="sortable" border="1" |
| | ! Step no. !! Clause of definition !! Who moves? !! What is chosen? !! Constraints on the choice !! Comment |
| | |- |
| | | 1 || For every <math>\varepsilon > 0</math> || Skeptic || <math>\varepsilon</math> || Must be positive || The "for every" corresponds to the idea that the move is made by the side that does ''not'' have a winning strategy, because we want to argue that the side that ''does'' have a winning strategy can win ''no matter what''. |
| | |- |
| | | 2 || there exists <math>\delta > 0</math> such that || Prover || <math>\delta</math> || Must be positive || The "there exists" corresponds to the idea that the move is made by the side that has a winning strategy, because that side gets to choose a favorable value of the variable (in this case <math>\delta</math>). |
| | |- |
| | | 3 || for all <math>x</math> satisfying <math>0 < |x - c| < \delta</math>, || Skeptic || <math>x</math> || Must be within the interval <math>(c - \delta,c) \cup (c,c + \delta)</math> || The "for all" corresponds to the idea that the move is made by the side that does ''not'' have a winning strategy, because we want to argue that the side that ''does'' have a winning strategy can win ''no matter what''. |
| | |- |
| | | 4 || we have <math>|f(x) - L| < \varepsilon</math> || Neither; it's time for the judge to decide || -- || If <math>f(x) \in (L - \varepsilon,L + \varepsilon)</math> (the condition that we desire) the prover wins. Else, the skeptic wins. || |
| | |} |
|
| |
|
| [[File:Epsilondeltagamepicture.png|1000px]] | | [[File:Epsilondeltagamepicture.png|1000px]] |
|
| |
|
| '''Slight subtlety regarding domain of definition''': The domain of definition issue leads to a couple of minor subtleties: | | '''Slight subtlety regarding domain of definition''': <toggledisplay>The domain of definition issue leads to a couple of minor subtleties: |
|
| |
|
| * A priori, it is possible that the <math>x</math> chosen by the skeptic is outside the domain of <math>f</math>, so it does not make sense to evaluate <math>f(x)</math>. In the definition given above, this would lead to the game being won by the skeptic. In particular, if <math>f</math> is not defined on the immediate left or right of <math>c</math>, the skeptic can always win by picking <math>x</math> outside the domain. | | * A priori, it is possible that the <math>x</math> chosen by the skeptic is outside the domain of <math>f</math>, so it does not make sense to evaluate <math>f(x)</math>. In the definition given above, this would lead to the game being won by the skeptic. In particular, if <math>f</math> is not defined on the immediate left or right of <math>c</math>, the skeptic can always win by picking <math>x</math> outside the domain. |
| Line 1,664: |
Line 1,752: |
| ** We could require (as part of the game rules) that the prover pick <math>\delta</math> such that <math>(c - \delta, c + \delta) \setminus \{ c \} \subseteq \operatorname{dom} f</math>. This pre-empts the problem of picking <math>x</math>-values outside the domain. | | ** We could require (as part of the game rules) that the prover pick <math>\delta</math> such that <math>(c - \delta, c + \delta) \setminus \{ c \} \subseteq \operatorname{dom} f</math>. This pre-empts the problem of picking <math>x</math>-values outside the domain. |
| ** We could require (as part of the game rules) that the skeptic pick <math>x</math> ''in'' the domain, i.e., pick <math>x</math> with <math>0 < |x - c| < \delta</math> and <math>x \in \operatorname{dom} f</math>. | | ** We could require (as part of the game rules) that the skeptic pick <math>x</math> ''in'' the domain, i.e., pick <math>x</math> with <math>0 < |x - c| < \delta</math> and <math>x \in \operatorname{dom} f</math>. |
| ** We could alter the rule so that if the skeptic picks <math>x</math> outside the domain, the prover wins (instead of the skeptic winning). | | ** We could alter the rule so that if the skeptic picks <math>x</math> outside the domain, the prover wins (instead of the skeptic winning).</toggledisplay> |
|
| |
|
| <center>{{#widget:YouTube|id=Kh253PUghFk}}</center> | | <center>{{#widget:YouTube|id=Kh253PUghFk}}</center> |
| Line 2,039: |
Line 2,127: |
| I explain the mathematical symbols.</toggledisplay> | | I explain the mathematical symbols.</toggledisplay> |
|
| |
|
| | ===Negation of limit statement and non-existence of limit=== |
| | |
| | We now consider the explicit description of the definition for the case that the skeptic has a winning strategy for the limit game for <math>\lim_{x \to c} f(x) = L</math>, i.e., for the limit statement being false. |
| | |
| | In words, the definition is: |
| | |
| | {{quotation|There exists <math>\varepsilon > 0</math> such that for every <math>\delta > 0</math>, there exists <math>x</math> satisfying <math>0 < |x - c| < \delta</math> and <math>|f(x) - L| \ge \varepsilon</math>.}} |
| | |
| | Let's review the definition in conjunction with the game along with a deeper semantic understanding of the steps: |
| | |
| | {| class="sortable" border="1" |
| | ! Step no. !! Clause of definition for original limit statement (i.e., prover has a winning strategy) !! Clause of definition for skeptic having a winning strategy !! Who moves? !! What is chosen? !! Constraints on the choice !! Comment |
| | |- |
| | | 1 || For every <math>\varepsilon > 0</math> || There exists <math>\varepsilon > 0</math> such that || Skeptic || <math>\varepsilon</math> || Must be positive || Whether we use "for every" or "there exists" depends on who we're rooting for. |
| | |- |
| | | 2 || there exists <math>\delta > 0</matH> such that || for every <math>\delta > 0</math>, || Prover || <math>\delta</math> || Must be positive || Whether we use "for every" or "there exists" depends on who we're rooting for. |
| | |- |
| | | 3 || for all <math>x \in \R</math> satisfying <math>0 < |x - c| < \delta</math>, || there exists <math>x \in \R</math> satisfying <math>0 < |x - c| < \delta</math> and || Skeptic || <math>x</math> || Must be within the interval <math>(c - \delta,c) \cup (c,c + \delta)</math> || Whether we use "for every" or "there exists" depends on who we're rooting for. |
| | |- |
| | | 4 || we have <math>|f(x) - L| < \varepsilon</math> || <math>|f(x) - L| \ge \varepsilon</math>. || Neither; it's time for the judge to decide || -- || If <math>f(x) \in (L - \varepsilon,L + \varepsilon)</math>, the prover wins. Else, the skeptic wins. || The conditions are negatives of one another. |
| | |} |
| <center>{{#widget:YouTube|id=N0U8Y11nlPk}}</center> | | <center>{{#widget:YouTube|id=N0U8Y11nlPk}}</center> |
|
| |
|
| Line 2,353: |
Line 2,462: |
|
| |
|
| # <math>f</math> is not ''defined'' around <math>c</math>, i.e., there is no <math>t > 0</math> for which <math>f</math> is defined on <math>(c - t, c + t) \setminus \{ c \}</math>. In this case, it does not even make sense to try taking a limit. | | # <math>f</math> is not ''defined'' around <math>c</math>, i.e., there is no <math>t > 0</math> for which <math>f</math> is defined on <math>(c - t, c + t) \setminus \{ c \}</math>. In this case, it does not even make sense to try taking a limit. |
| # <math>f</math> is defined around <math>c</math>, around <math>c</math>, i.e., there is <math>t > 0</math> for which <math>f</math> is defined on <math>(c - t, c + t) \setminus \{ c \}</math>. So, it does make sense to try taking a limit. However, the limit still does not exist. | | # <math>f</math> is defined around <math>c</math>, except possibly at <math>c</math>, i.e., there is <math>t > 0</math> for which <math>f</math> is defined on <math>(c - t, c + t) \setminus \{ c \}</math>. So, it does make sense to try taking a limit. However, the limit still does not exist. |
|
| |
|
| The formulation of the latter case is as follows: | | The formulation of the latter case is as follows: |
| Line 2,366: |
Line 2,475: |
|
| |
|
| does not exist. The skeptic's winning strategy is as follows: regardless of the <math>L</math> chosen by the prover, pick a fixed <math>\varepsilon < 1</math> (independent of <math>L</math>, so <math>\varepsilon</math> can be decided in advance of the game -- note that the skeptic could even pick <math>\varepsilon = 1</math> and the strategy would still work). After the prover has chosen a value <math>\delta</math>, find a value <math>x \in (0 - \delta,0 + \delta) \setminus \{ 0 \}</math> such that the <math>\sin(1/x)</math> function value lies outside <math>(L - \varepsilon,L + \varepsilon)</math>. This is possible because the interval <math>(L - \varepsilon,L + \varepsilon)</math> has width <math>2 \varepsilon</math>, hence cannot cover the entire interval <math>[-1,1]</math>, which has width 2. However, the range of the <math>\sin(1/x)</math> function on <math>(0 - \delta,0 + \delta) \setminus \{ 0 \}</math> is all of <math>[-1,1]</math>. | | does not exist. The skeptic's winning strategy is as follows: regardless of the <math>L</math> chosen by the prover, pick a fixed <math>\varepsilon < 1</math> (independent of <math>L</math>, so <math>\varepsilon</math> can be decided in advance of the game -- note that the skeptic could even pick <math>\varepsilon = 1</math> and the strategy would still work). After the prover has chosen a value <math>\delta</math>, find a value <math>x \in (0 - \delta,0 + \delta) \setminus \{ 0 \}</math> such that the <math>\sin(1/x)</math> function value lies outside <math>(L - \varepsilon,L + \varepsilon)</math>. This is possible because the interval <math>(L - \varepsilon,L + \varepsilon)</math> has width <math>2 \varepsilon</math>, hence cannot cover the entire interval <math>[-1,1]</math>, which has width 2. However, the range of the <math>\sin(1/x)</math> function on <math>(0 - \delta,0 + \delta) \setminus \{ 0 \}</math> is all of <math>[-1,1]</math>. |
| | |
| | {{quotation|Crucially, the inability of the prover to trap the function value close to any point as <math>x \to 0</math> is the reason the limit fails to exist.}} |
|
| |
|
| [[File:Sin1byxlimitat0.png|800px]] | | [[File:Sin1byxlimitat0.png|800px]] |
| Line 2,374: |
Line 2,485: |
|
| |
|
| Full timed transcript: <toggledisplay> | | Full timed transcript: <toggledisplay> |
| 0:00:15.500,0:00:19.140 | | 0:00:31.170,0:00:38.170 |
| Vipul: Okay. This talk is going to be about | | Vipul: Ok, so this talk is going to be about |
| certain misconceptions | | why under certain circumstances limits don't exist |
| | |
| | 0:00:39.800,0:00:46.800 |
| | We are going to take this example of a function |
| | which is defined like this: sin of one over x |
|
| |
|
| 0:00:19.140,0:00:22.440 | | 0:00:47.699,0:00:51.360 |
| that people have regarding limits and these | | Obviously, that definition doesn't work |
| are misconceptions that
| | when x equals zero. |
|
| |
|
| 0:00:22.440,0:00:25.840 | | 0:00:51.360,0:00:57.260 |
| people generally acquire after...
| | So this is a function defined only for all non-zero |
| | reals. |
|
| |
|
| 0:00:25.840,0:00:29.180 | | 0:00:57.260,0:01:01.050 |
| These are not the misconceptions that
| | The goal is to figure out what the limit as |
| people have before studying limits,
| | x approaches 0 of f(x) is. |
|
| |
|
| 0:00:29.180,0:00:32.730 | | 0:01:01.050,0:01:06.630 |
| these are misconceptions you might have after
| | Here is a graph of the function. This is a |
| studying limits,
| | y axis, and x axis. |
|
| |
|
| 0:00:32.730,0:00:35.059 | | 0:01:06.630,0:01:08.490 |
| after studying the epsilon delta definition.
| | The function looks like this. |
|
| |
|
| 0:00:35.059,0:00:38.550 | | 0:01:08.490,0:01:10.680 |
| I'm going to describe these misconceptions
| | It is oscillatory. |
| in terms of the limit game,
| | |
| | 0:01:10.680,0:01:16.270 |
| | As you approach zero it oscillates more, faster |
| | and faster. |
|
| |
|
| 0:00:38.550,0:00:41.900 | | 0:01:16.270,0:01:19.070 |
| the prover skeptic game of the limit. Though | | What are the upper and lower limits of oscillation? |
| the misconceptions
| |
|
| |
|
| 0:00:41.900,0:00:45.850 | | 0:01:19.070,0:01:25.580 |
| themselves can be, sort of, don't depend
| | Actually all these things should be the same |
| on the understanding of the
| | height. |
|
| |
|
| 0:00:45.850,0:00:49.059 | | 0:01:25.580,0:01:29.760 |
| game but to understand exactly what's
| | My drawing wasn't good, but, it should all |
| happening, it's better to think
| | be the same height, above and below. |
|
| |
|
| 0:00:49.059,0:00:51.010 | | 0:01:29.760,0:01:31.290 |
| of it in terms of the game.
| | What are these upper and lower limits? [ANSWER!] |
|
| |
|
| 0:00:51.010,0:00:55.370 | | 0:01:31.290,0:01:32.790 |
| First recall the definition. So limit as x
| | Rui: 1 and -1. |
| approaches c of f(x) is a
| |
|
| |
|
| 0:00:55.370,0:01:01.629 | | 0:01:32.790,0:01:39.790 |
| number L; so c and L are both numbers, real
| | Vipul: So the lower limit is negative one |
| numbers. f is a function,
| | and the upper limit is one. Ok, good. |
|
| |
|
| 0:01:01.629,0:01:06.380 | | 0:01:39.829,0:01:46.829 |
| x is approaching c. And we said this is true
| | So what does it mean, what is the limit at |
| if the following -- for
| | zero for this function? [ANSWER!] |
|
| |
|
| 0:01:06.380,0:01:10.180 | | 0:01:46.850,0:01:53.850 |
| every epsilon greater than zero, there exists
| | This is where...you need to really think, so |
| a delta greater than
| | I might say ok the limit is, looks like it's zero. |
|
| |
|
| 0:01:10.180,0:01:14.800 | | 0:01:58.259,0:01:58.509 |
| zero such that for all x which are given delta
| |
| distance of c, f(x) is
| |
|
| |
|
| 0:01:14.800,0:01:17.590 | | 0:01:58.469,0:02:04.749 |
| within epsilon distance of L. Okay?
| | At zero, you say that looks neat, that looks |
| | right because you see when the x value approaches, |
|
| |
|
| 0:01:17.590,0:01:24.590 | | 0:02:04.749,0:02:09.190 |
| Now, how do we describe this in terms for
| | comes close to zero, the f(x) value also comes |
| limit game?
| | close to zero. |
|
| |
|
| 0:01:26.530,0:01:33.530 | | 0:02:09.190,0:02:12.700 |
| KM: So, skeptic starts off with the first
| | It keeps oscillating between -1and 1, |
| part of the definition.
| | and it keeps coming. |
|
| |
|
| 0:01:34.990,0:01:38.189 | | 0:02:12.700,0:02:19.700 |
| Vipul: By picking the epsilon? Okay, that's
| | I draw a very small ball around zero, like |
| the thing written in
| | that. |
|
| |
|
| 0:01:38.189,0:01:42.939 | | 0:02:19.780,0:02:22.700 |
| black. What's the skeptic trying to do? What's the
| | The function is going to keep entering this |
| goal of the skeptic?
| | ball. |
|
| |
|
| 0:01:42.939,0:01:49.100 | | 0:02:22.700,0:02:27.060 |
| KM: To try and pick an epsilon that would
| | A ball or a square one or whatever. |
| not work.
| | |
| | 0:02:27.060,0:02:34.060 |
| | A very small neighborhood of this origin point |
| | here in this two-dimensional picture. |
|
| |
|
| 0:01:49.100,0:01:53.450 | | 0:02:35.230,0:02:40.459 |
| Vipul: So the goal of the skeptic is to try
| | The function graph is going to enter that |
| to show that the statement is false.
| | repeatedly. |
|
| |
|
| 0:01:53.450,0:01:54.100 | | 0:02:40.459,0:02:42.010 |
| KM: Yeah.
| | Do you think the limit is zero? [ANSWER!] |
|
| |
|
| 0:01:54.100,0:01:57.790 | | 0:02:42.010,0:02:42.830 |
| Vipul: Right? In this case the skeptic should
| | Rui: No. |
| try to start by choosing
| |
|
| |
|
| 0:01:57.790,0:02:02.220 | | 0:02:42.830,0:02:46.860 |
| an epsilon that is really -- the goal of
| | Vipul: No? Why not? Isn't it coming really |
| the skeptic is to pick an
| | close to zero? |
|
| |
|
| 0:02:02.220,0:02:04.500 | | 0:02:46.860,0:02:47.430 |
| epsilon that's really small, what is the
| | Rui: Sometimes. |
| skeptic trying to challenge
| |
|
| |
|
| 0:02:04.500,0:02:07.920 | | 0:02:47.430,0:02:49.140 |
| the prover into doing by picking the epsilon?
| | Vipul: What do you mean "sometimes?" |
| The skeptic is trying to
| |
|
| |
|
| 0:02:07.920,0:02:11.959 | | 0:02:49.140,0:02:56.140 |
| challenge the prover into trapping the function
| | Rui: It means sometimes it is real close to |
| close to L when x is | | zero and then it flies away. |
|
| |
|
| 0:02:11.959,0:02:17.040 | | 0:02:56.870,0:03:03.870 |
| close to c. And the skeptic specifies what
| | Vipul: Ok, "flies away." [Hmm] So what's |
| is meant by "close to L" is | | your objection? What is not happening? |
|
| |
|
| 0:02:17.040,0:02:19.860 | | 0:03:04.019,0:03:06.010 |
| by the choice of epsilon. Okay?
| | Rui: We can not trap. |
|
| |
|
| 0:02:19.860,0:02:24.900 | | 0:03:06.010,0:03:07.239 |
| When picking epsilon the skeptic is
| | Vipul: We cannot trap... |
| effectively picking this interval, L -
| |
|
| |
|
| 0:02:24.900,0:02:30.700 | | 0:03:07.239,0:03:11.909 |
| epsilon, L + epsilon). Okay? And basically
| | Rui: ...trap it in a neighborhood of zero. |
| that's what the skeptic is
| |
|
| |
|
| 0:02:30.700,0:02:33.680 | | 0:03:11.909,0:03:18.480 |
| doing. The prover is then picking a delta.
| | Vipul: Function not trapped. |
| What is the goal of the
| |
|
| |
|
| 0:02:33.680,0:02:36.239 | | 0:03:18.480,0:03:20.110 |
| prover in picking the delta? The prover is
| | What should the limit be if it is not zero? |
| saying, "Here's how I can
| |
|
| |
|
| 0:02:36.239,0:02:40.099 | | 0:03:20.110,0:03:24.849 |
| trap the function within that interval. I'm
| | Should it be half, two-thirds, what should |
| going to pick a delta and
| | the limit be? [ANSWER!] |
|
| |
|
| 0:02:40.099,0:02:43.520 | | 0:03:24.849,0:03:31.849 |
| my claim is that if the x value within delta distance of c, except the
| | (I'll explain this later), what do you think |
| | the limit should be? |
|
| |
|
| 0:02:43.520,0:02:47.000 | | 0:03:34.659,0:03:36.730 |
| point c itself, so my claim is for any x value
| | Rui: It doesn't have a limit. |
| there the function is
| |
|
| |
|
| 0:02:47.000,0:02:48.260 | | 0:03:36.730,0:03:38.299 |
| trapped in here."
| | Vipul: It doesn't have a limit. |
|
| |
|
| 0:02:48.260,0:02:52.819 | | 0:03:38.299,0:03:39.790 |
| So, the prover picks the delta and then the
| | Ok, so what does that mean? |
| skeptic tries to meet the
| |
|
| |
|
| 0:02:52.819,0:02:56.709 | | 0:03:39.790,0:03:45.290 |
| prover's claim or rather, test the prover's
| | Whatever limit you claim the function has |
| claim by picking an x | | you are wrong...If you claim the function had |
|
| |
|
| 0:02:56.709,0:02:59.670 | | 0:03:45.290,0:03:49.170 |
| which is within the interval specified by
| | any numerical limit, if you claim if it is half you |
| the prover and then they
| | are wrong. |
|
| |
|
| 0:02:59.670,0:03:03.379 | | 0:03:49.170,0:03:50.640 |
| both check whether f(x) is within epsilon
| | If you claim minus half you are wrong. |
| distance [of L]. If it is
| |
|
| |
|
| 0:03:03.379,0:03:07.940 | | 0:03:50.640,0:03:52.720 |
| then the prover wins and if it is not, if
| | If you claim the limit is 50, you are wrong. |
| this [|f(x) - L|]is not less
| |
|
| |
|
| 0:03:07.940,0:03:09.989 | | 0:03:52.720,0:03:54.959 |
| than epsilon then the skeptic wins. Okay?
| | Whatever claim you make about the limit, |
| | you are wrong. |
|
| |
|
| 0:03:09.989,0:03:13.659 | | 0:03:54.959,0:04:00.780 |
| So, the skeptic is picking the neighborhood | | So let's try to think of this in terms of the |
| of the target point which
| | game between a prover and a skeptic. |
|
| |
|
| 0:03:13.659,0:03:17.030 | | 0:04:00.780,0:04:02.730 |
| in this case is just the open interval of
| | (You should go and review that video |
| radius epsilon, the prover
| |
|
| |
|
| 0:03:17.030,0:03:21.940 | | 0:04:02.730,0:04:09.730 |
| is picking the delta which is effectively the
| | or read the corresponding material to understand |
| neighborhood of the domain
| | what I am going to say.) |
|
| |
|
| 0:03:21.940,0:03:25.760 | | 0:04:09.829,0:04:13.969 |
| point except the point c as I've said open
| | It's good if you have also seen the video |
| interval (c - delta, c +
| | on the definition of limit statement being |
|
| |
|
| 0:03:25.760,0:03:30.870 | | 0:04:13.969,0:04:17.709 |
| delta) excluding c and then the skeptic picks
| | false, which builds on that. |
| an x in the neighborhood
| |
|
| |
|
| 0:03:30.870,0:03:35.700 | | 0:04:17.709,0:04:21.620 |
| specified by prover and if the function value
| | What I am now asking you, what does it mean |
| is within the interval
| | to say the limit does not exist? |
|
| |
|
| 0:03:35.700,0:03:38.830 | | 0:04:21.620,0:04:23.980 |
| specified by the skeptic then the prover wins.
| | As x approaches c [limit] of f(x) does not exist. |
|
| |
|
| 0:03:38.830,0:03:41.989 | | 0:04:23.980,0:04:27.810 |
| Now, what does it mean to say the statement
| | Here c is zero, but that is not relevant... |
| is true in terms of the | | that is not necessary for the definition. |
|
| |
|
| 0:03:41.989,0:03:43.080 | | 0:04:27.810,0:04:32.910 |
| game?
| | Well it is the usual way we say that the |
| | limit statement is false except we need to |
|
| |
|
| 0:03:43.080,0:03:50.080 | | 0:04:32.910,0:04:37.170 |
| KM: So, it means that the prover is always
| | add one step in the beginning, which is for |
| going to win the game.
| | every L in R [the reals]. |
| | |
| | 0:04:37.170,0:04:42.460 |
| | It says that for every L in R [the reals] the statement |
| | limit x approaches c, f(x) equals L, is false. |
|
| |
|
| 0:03:51.849,0:03:55.629 | | 0:04:42.460,0:04:43.900 |
| Vipul: Well, sort of. I mean the prover may
| | So how does it read? |
| play it stupidly. The
| |
|
| |
|
| 0:03:55.629,0:04:00.750 | | 0:04:43.900,0:04:48.220 |
| prover can win the game if the prover plays
| | It says, for every L in R [the reals] there exists epsilon |
| well. So, the prover has a
| | greater than zero such that for every delta |
|
| |
|
| 0:04:00.750,0:04:03.230 | | 0:04:48.220,0:04:55.030 |
| winning strategy for the game. Okay?
| | greater than zero there exists x, within the |
| | delta neighborhood of c such that f(x) is |
|
| |
|
| 0:04:05.230,0:04:10.299 | | 0:04:55.030,0:04:58.590 |
| The statement is true if the prover has a
| | not in the epsilon neighborhood of L. |
| winning strategy for [the
| |
|
| |
|
| 0:04:10.299,0:04:14.090 | | 0:04:58.590,0:05:05.590 |
| game] and that means the prover has a way | | How would you interpret this in terms of a |
| of playing the game such that
| | game between a prover and a skeptic?[ANSWER, THINKING ALONG!] |
|
| |
|
| 0:04:14.090,0:04:17.320 | | 0:05:06.470,0:05:11.570 |
| whatever the skeptic does the prover is going
| | Rui: For every limit the prover proposes... |
| to win the game. The
| |
|
| |
|
| 0:04:17.320,0:04:20.789 | | 0:05:11.570,0:05:16.420 |
| statement is considered false if the skeptic
| | Vipul: This is not quite the same as the limit |
| has a winning strategy
| | game which you may have seen in a previous |
|
| |
|
| 0:04:20.789,0:04:23.370 | | 0:05:16.420,0:05:21.170 |
| for the game which means the skeptic has a
| | video which was assuming that the limit was |
| way of playing so that
| | already given as a part of the game. |
|
| |
|
| 0:04:23.370,0:04:25.729 | | 0:05:21.170,0:05:28.170 |
| whatever the prover does the skeptic can win
| | This is sort of a somewhat more general game or |
| the game. | | a more meta game where part of the game |
|
| |
|
| 0:04:25.729,0:04:27.599 | | 0:05:28.420,0:05:31.950 |
| Or if the game doesn't make sense at all
| | is also the prover trying to specify what |
| ...
| | the limit should be. |
|
| |
|
| 0:04:27.599,0:04:29.460 | | 0:05:31.950,0:05:37.100 |
| maybe the function is not defined on
| | The first step the prover plays, the prover |
| | is in black, skeptic is in red. |
|
| |
|
| 0:04:29.460,0:04:31.050 | | 0:05:37.100,0:05:43.290 |
| the immediate left and right of c. | | The first step the prover plays, proposes |
| | a value of the limit. Then? |
|
| |
|
| 0:04:31.050,0:04:32.370 | | 0:05:43.290,0:05:47.280 |
| If the function isn't defined then we
| | Rui: The skeptic chooses an epsilon. |
|
| |
|
| 0:04:32.370,0:04:34.160 | | 0:05:47.280,0:05:50.020 |
| cannot even make sense of the statement.
| | Vipul: What's the goal of the skeptic in choosing |
| | the epsilon? |
|
| |
|
| 0:04:34.160,0:04:36.990 | | 0:05:50.020,0:05:56.740 |
| Either way -- the skeptic has a winning strategy
| | The goal of the skeptic is.. so let's say |
| | the prover chose a limit value L here, that's |
|
| |
|
| 0:04:36.990,0:04:37.770 | | 0:05:56.740,0:05:58.470 |
| or the game doesn't make sense --
| | numerical value L here. |
|
| |
|
| 0:04:41.770,0:04:43.470 | | 0:05:58.470,0:06:00.050 |
| then the statement is false.
| | The skeptic picks epsilon. |
| | |
| | 0:06:00.050,0:06:06.650 |
| | The skeptic will pick epsilon, which means |
| | the skeptic is picking this band from L minus |
|
| |
|
| 0:04:43.470,0:04:47.660 | | 0:06:06.650,0:06:12.400 |
| If the prover has a winning strategy
| | epsilon to L plus epsilon. |
| the statement is true.
| |
|
| |
|
| 0:04:47.660,0:04:54.660 | | 0:06:12.400,0:06:14.270 |
| With this background in mind let's look
| | Now what does the prover try to do? |
| at some common misconceptions.
| |
|
| |
|
| 0:04:56.540,0:05:03.540 | | 0:06:14.270,0:06:19.000 |
| Okay. Let's say we are trying to prove that
| | The prover tries to pick a delta. What is |
| the limit as x approaches
| | the prover trying to do? |
|
| |
|
| 0:05:27.620,0:05:31.530 | | 0:06:19.000,0:06:24.490 |
| 2 of x^2 is 4, so is that statement correct?
| | Find a neighborhood of c, such that the |
| The statement we're
| | function in that neighborhood of c the function |
|
| |
|
| 0:05:31.530,0:05:32.060 | | 0:06:24.490,0:06:28.370 |
| trying to prove?
| | is trapped within epsilon of L. |
|
| |
|
| 0:05:32.060,0:05:32.680 | | 0:06:28.370,0:06:32.740 |
| KM: Yes.
| | So in our case, c is zero in this example, |
| | so the prover will be trying to pick a neighborhood |
|
| |
|
| 0:05:32.680,0:05:35.960 | | 0:06:32.740,0:06:39.740 |
| Vipul: That's correct. Because in fact x^2
| | of zero, is something like... zero plus delta |
| is a continuous function
| | on the right and zero minus delta on the left. |
|
| |
|
| 0:05:35.960,0:05:40.160 | | 0:06:44.620,0:06:45.750 |
| and the limit of a continuous function at
| | What's the goal of the prover? |
| the point is just the
| |
|
| |
|
| 0:05:40.160,0:05:43.030 | | 0:06:45.750,0:06:50.840 |
| value at the point and 2^2 is 4. But we're
| | To say that whenever x is in this interval, |
| going to now try to prove
| | for all x, |
|
| |
|
| 0:05:43.030,0:05:48.530 | | 0:06:50.840,0:06:53.500 |
| this formally using the epsilon-delta definition
| | The prover is trying to say that all for x |
| of limit, okay? Now
| | in here, the function [difference from L] is less than epsilon. |
|
| |
|
| 0:05:48.530,0:05:51.229 | | 0:06:53.500,0:06:56.170 |
| in terms of the epsilon-delta definition or
| | The skeptic who is trying to disprove that. |
| rather in terms of this
| |
|
| |
|
| 0:05:51.229,0:05:55.160 | | 0:06:56.170,0:06:59.060 |
| game setup, what we need to do is we need
| | What does the skeptic need to do? |
| to describe a winning
| |
|
| |
|
| 0:05:55.160,0:06:01.460 | | 0:06:59.060,0:07:03.900 |
| strategy for the prover. Okay? We need to
| | Rui: Every time the prover finds an x. |
| describe delta in terms of
| |
|
| |
|
| 0:06:01.460,0:06:05.240 | | 0:07:03.900,0:07:07.540 |
| epsilon. The prover essentially ... the only
| | Vipul: Well the prover finds, picks the delta, |
| move the prover makes is
| | what does the skeptic try to do? |
|
| |
|
| 0:06:05.240,0:06:09.130 | | 0:07:07.540,0:07:08.480 |
| this choice of delta. Right? The skeptic picked
| | Rui: Just pick an x. |
| epsilon, the prover
| |
|
| |
|
| 0:06:09.130,0:06:12.810 | | 0:07:08.480,0:07:10.550 |
| picked delta then the skeptic picks x and
| | Vipul: Picks an x such that the function... |
| then they judge who won. The
| |
|
| |
|
| 0:06:12.810,0:06:15.810 | | 0:07:10.550,0:07:12.140 |
| only choice the prover makes is the choice
| | Rui: Is out of the... |
| of delta, right?
| |
|
| |
|
| 0:06:15.810,0:06:16.979 | | 0:07:12.140,0:07:13.960 |
| KM: Exactly.
| | Vipul: Is outside that thing. |
|
| |
|
| 0:06:16.979,0:06:20.080 | | 0:07:13.960,0:07:24.960 |
| Vipul: The prover chooses the delta in terms
| | Let me make this part a little bit more...so |
| of epsilon.
| | here you have... the same colors. |
|
| |
|
| 0:06:20.080,0:06:24.819 | | 0:07:25.150,0:07:41.150 |
| So, here is my strategy. My strategy is I'm
| | This is |
| going to choose delta as,
| | the axis...The skeptic...The prover has picked |
| | this point and the skeptic has picked epsilon. |
|
| |
|
| 0:06:24.819,0:06:29.509 | | 0:07:41.780,0:07:46.670 |
| I as a prover is going to choose delta as
| | So this is L plus epsilon, L minus epsilon. |
| epsilon over the absolute | |
|
| |
|
| 0:06:29.509,0:06:33.690 | | 0:07:46.670,0:07:50.460 |
| value of x plus 2 [|x + 2|]. Okay?
| | The prover is now, it so happens that c is |
| | zero here. |
|
| |
|
| 0:06:33.690,0:06:36.880 | | 0:07:50.460,0:07:56.690 |
| Now, what I want to show that this strategy
| | So that everything is happening near the y |
| works. So, what I'm aiming
| | axis. |
|
| |
|
| 0:06:36.880,0:06:39.840 | | 0:07:56.690,0:08:03.690 |
| is that if ... so let me just finish this
| | Now, the prover wants to pick a delta, the |
| and then you can tell me where
| | prover wants to pick, like this, should be |
|
| |
|
| 0:06:39.840,0:06:43.419 | | 0:08:07.320,0:08:07.910 |
| I went wrong here, okay? I'm claiming that
| | the same. |
| this strategy works which
| |
|
| |
|
| 0:06:43.419,0:06:47.130 | | 0:08:07.910,0:08:14.910 |
| means I'm claiming that if the skeptic now
| | So this is c plus delta which c is zero, so |
| picks any x which is within
| | zero plus delta and zero minus delta. |
|
| |
|
| 0:06:47.130,0:06:54.130 | | 0:08:17.810,0:08:21.960 |
| delta distance of 2; the target point,
| | Now, under what conditions...What happens |
| | next? |
|
| |
|
| 0:06:56.710,0:07:01.490 | | 0:08:21.960,0:08:28.240 |
| then the function value is within epsilon
| | The prover is implicitly trying to claim that |
| distance of 4, the claimed
| | the function, when the x value is close here, |
|
| |
|
| 0:07:01.490,0:07:04.080 | | 0:08:28.240,0:08:30.520 |
| limit. That's what I want to show.
| | the function value is trapped here. |
|
| |
|
| 0:07:04.080,0:07:08.300 | | 0:08:30.520,0:08:35.089 |
| Now is that true? Well, here's how I do
| | What the skeptic wants to show is that, that's |
| it. I think, I started by
| | not true. |
|
| |
|
| 0:07:08.300,0:07:13.539 | | 0:08:35.089,0:08:39.830 |
| picking this expression, I factored it as
| | If it isn't true, in order to do that, the |
| |x - 2||x + 2|. The absolute
| | skeptic should pick a value of x. |
|
| |
|
| 0:07:13.539,0:07:16.810 | | 0:08:39.830,0:08:46.830 |
| value of product is the product of the absolute | | So the skeptic needs to pick a value of x |
| values so this can be
| | somewhere in this interval such that at that |
| | |
| | 0:08:48.110,0:08:55.110 |
| | value of f(x)...let me just make the x axis...so |
| | the skeptic wants to pick a value of x, maybe |
|
| |
|
| 0:07:16.810,0:07:21.599 | | 0:08:59.209,0:09:06.209 |
| split like that. Now I see, while we know
| | its somewhere here, such that when you evaluate |
| that |x - 2| is less than
| | the function at x it lies outside. |
|
| |
|
| 0:07:21.599,0:07:24.979 | | 0:09:07.269,0:09:11.720 |
| delta and this is a positive thing. So we
| | If when you evaluate the function at x, and it lies |
| can either less than delta
| | outside this strip then the skeptic wins and |
|
| |
|
| 0:07:24.979,0:07:31.979 | | 0:09:11.720,0:09:16.290 |
| times absolute value x plus 2. Right? And
| | if the value of the function of x is inside |
| this delta is epsilon over
| | the strip then the prover wins. |
|
| |
|
| 0:07:35.599,0:07:37.620 | | 0:09:16.290,0:09:23.290 |
| |x + 2| and we get epsilon.
| | Now looking back at this function, the question |
| | is, can the prover pick an L such that regardless, |
|
| |
|
| 0:07:37.620,0:07:40.460 | | 0:09:25.209,0:09:31.779 |
| So, this thing equals something, less than
| | so can the prover pick a value of L such that...Is |
| something, equals
| | this whole thing coming? |
|
| |
|
| 0:07:40.460,0:07:43.580 | | 0:09:31.779,0:09:37.860 |
| something, equals something, you have a chain
| | Such that regardless of the epsilon that the |
| of things, there's one
| | skeptic picks, there exists a delta such that |
|
| |
|
| 0:07:43.580,0:07:47.720 | | 0:09:37.860,0:09:44.439 |
| step that you have less than. So overall we
| | for all x the function is trapped? Or is it |
| get that this expression,
| | instead true that the skeptic will win? (i.e.) Is |
|
| |
|
| 0:07:47.720,0:07:53.740 | | 0:09:44.439,0:09:50.579 |
| this thing is less than epsilon. So, we have
| | it true that whatever L the prover picks there |
| shown that whatever x the
| | exists an epsilon, since the skeptic picks |
|
| |
|
| 0:07:53.740,0:08:00.370 | | 0:09:50.579,0:09:57.360 |
| skeptic would pick, the function value lies
| | an epsilon, such that whatever delta the prover |
| within the epsilon
| | picks the function in not in fact, trapped |
|
| |
|
| 0:08:00.370,0:08:05.030 | | 0:09:57.360,0:10:00.399 |
| distance of the claimed limit. Whatever the
| | here. What do you think looking at the picture |
| skeptic picks (x within the
| | here? |
|
| |
|
| 0:08:05.030,0:08:09.240 | | 0:10:00.399,0:10:05.329 |
| delta distance of the target point).
| | Can you trap the function in a rectangle |
| | like this? [ANSWER!] |
|
| |
|
| 0:08:09.240,0:08:16.240 | | 0:10:05.329,0:10:06.100 |
| Does this strategy work? Is this a proof?
| | Rui: No. |
| What's wrong with this?
| |
|
| |
|
| 0:08:24.270,0:08:31.270 | | 0:10:06.100,0:10:09.930 |
| Do you think there's anything wrong
| | Vipul: Well, not if it is a very small rectangle. |
| with the algebra down here?
| |
|
| |
|
| 0:08:33.510,0:08:40.510 | | 0:10:09.930,0:10:16.930 |
| KM: Well, we said that ...
| | What should the skeptic's strategy be? |
|
| |
|
| 0:08:40.910,0:08:47.910 | | 0:10:17.060,0:10:23.930 |
| Vipul: So, is there anything wrong in the
| | The claim is that the limit does not exist, |
| algebra here? This is this,
| | that is the claim. |
|
| |
|
| 0:08:50.160,0:08:51.740 | | 0:10:23.930,0:10:25.990 |
| this is less than delta, delta ... So, this | | The claim is that this limit doesn't exist. |
| part
| |
|
| |
|
| 0:08:51.740,0:08:52.089 | | 0:10:25.990,0:10:29.750 |
| seems fine, right?
| | What is the skeptic's strategy? |
|
| |
|
| 0:08:52.089,0:08:52.339 | | 0:10:29.750,0:10:31.990 |
| KM: Yes.
| | What do you mean by skeptic strategy? |
|
| |
|
| 0:08:52.330,0:08:55.640 | | 0:10:31.990,0:10:37.370 |
| Vipul: There's nothing wrong in the algebra
| | Well, the skeptic should have some strategy |
| here. So, what could be
| | that works, so the skeptic should pick an |
|
| |
|
| 0:08:55.640,0:09:00.310 | | 0:10:37.370,0:10:43.290 |
| wrong? Our setup seems fine. If the x value
| | epsilon that is smart and then the skeptic |
| is within delta distance
| | should pick an x that works. |
|
| |
|
| 0:09:00.310,0:09:03.350 | | 0:10:43.290,0:10:50.209 |
| of 2 then the function value is within epsilon
| | What epsilon should the skeptic pick? Suppose |
| this is 4. That's
| | the skeptic picks epsilon as 50 million, |
|
| |
|
| 0:09:03.350,0:09:05.360 | | 0:10:50.209,0:10:52.050 |
| exactly what we want to prove, correct?
| | is that a winning strategy? |
|
| |
|
| 0:09:05.360,0:09:11.120 | | 0:10:52.050,0:10:52.790 |
| So, there's nothing wrong this point onward.
| | Rui: No. |
| So, the error happened
| |
|
| |
|
| 0:09:11.120,0:09:14.440 | | 0:10:52.790,0:10:53.899 |
| somewhere here. Where do you think that part
| | Vipul: Why not? |
| you think what is wrong
| |
|
| |
|
| 0:09:14.440,0:09:21.160 | | 0:10:53.899,0:10:58.300 |
| here? In the strategy choice step? What do
| | Rui: He should pick something between -1 and |
| you think went wrong in the
| | 1, right? |
|
| |
|
| 0:09:21.160,0:09:24.010 | | 0:10:58.300,0:11:01.920 |
| strategy choice step?
| | Vipul: Well epsilon is a positive number so |
| | what do you mean? |
|
| |
|
| 0:09:24.010,0:09:28.850 | | 0:11:01.920,0:11:04.600 |
| What? Okay, so let's go over the game. Skeptic
| | Rui: Oh, anything between one, smaller. |
| will choose the epsilon,
| |
|
| |
|
| 0:09:28.850,0:09:29.760 | | 0:11:04.600,0:11:05.230 |
| then?
| | Vipul: Smaller than... |
|
| |
|
| 0:09:29.760,0:09:35.130 | | 0:11:05.230,0:11:08.999 |
| KM: Then the prover chooses delta.
| | Rui: Less than one. Epsilon. |
|
| |
|
| 0:09:35.130,0:09:36.080 | | 0:11:08.999,0:11:12.470 |
| Vipul: Prover chooses delta. Then? | | Vipul: Less than one. Why will that work? |
|
| |
|
| 0:09:36.080,0:09:39.529 | | 0:11:12.470,0:11:19.470 |
| KM: Then the skeptic has to choose the x value.
| | Rui: Because even if it is less than one then |
| | anything, no matter what kind of delta... |
|
| |
|
| 0:09:39.529,0:09:42.470 | | 0:11:20.930,0:11:27.930 |
| Vipul: x value. So, when the prover is deciding | | Vipul: Whatever L the prover picked...What |
| the strategy, when the
| | is the width of this interval? The distance |
|
| |
|
| 0:09:42.470,0:09:45.860 | | 0:11:28.209,0:11:29.589 |
| prover is choosing the delta, what information
| | from the top and the bottom is? |
| does the prover have?
| |
|
| |
|
| 0:09:45.860,0:09:48.410 | | 0:11:29.589,0:11:30.279 |
| KM: He just has the information epsilon.
| | Rui: 2 |
|
| |
|
| 0:09:48.410,0:09:50.500 | | 0:11:30.279,0:11:30.980 |
| Vipul: Just the information on epsilon. So? | | Vipul: [2 times] epsilon. |
|
| |
|
| 0:09:50.500,0:09:57.060 | | 0:11:30.980,0:11:31.680 |
| KM: So, in this case the mistake was that
| | Rui: [2 times] epsilon. |
| because he didn't know the x value yet?
| |
|
| |
|
| 0:09:57.060,0:10:03.100 | | 0:11:31.680,0:11:38.680 |
| Vipul: The strategy cannot depend on x. | | Vipul: 2 epsilon. If epsilon |
| | is less than one, the skeptic's strategy is |
| | pick epsilon less than one any epsilon. |
|
| |
|
| 0:10:03.100,0:10:04.800 | | 0:11:43.089,0:11:50.089 |
| KM: Yeah.
| | The skeptic can fix epsilon in the beginning, maybe pick |
| | epsilon as 0.1 or something, but any epsilon |
|
| |
|
| 0:10:04.800,0:10:09.790 | | 0:11:50.610,0:11:52.019 |
| Vipul: So, the prover is sort of picking the
| | less than one will do. |
| delta based on x but the
| |
|
| |
|
| 0:10:09.790,0:10:12.660 | | 0:11:52.019,0:11:59.019 |
| prover doesn't know x at this stage when
| | In fact epsilon equal to one will do. Let |
| picking the delta. The delta
| | us play safe and pick epsilon as 0.1. |
|
| |
|
| 0:10:12.660,0:10:15.910 | | 0:11:59.810,0:12:00.999 |
| that the prover chooses has to be completely
| | Why does it work? |
| a function of epsilon
| |
|
| |
|
| 0:10:15.910,0:10:19.680 | | 0:12:00.999,0:12:06.600 |
| alone, it cannot depend on the future moves
| | Because this 2 epsilon cannot include both |
| of the skeptic because the
| | one and minus one. |
|
| |
|
| 0:10:19.680,0:10:23.700 | | 0:12:06.600,0:12:12.649 |
| prover cannot read the skeptic's mind. Okay?
| | It cannot cover this entire thing because |
| And doesn't know what the
| | this has width two, from one to minus one. |
|
| |
|
| 0:10:23.700,0:10:24.800 | | 0:12:12.649,0:12:17.589 |
| skeptic plans to do. | | If the skeptic picks an epsilon less than |
| | one, regardless of the L the prover has tried, |
|
| |
|
| 0:10:24.800,0:10:31.800 | | 0:12:17.589,0:12:23.079 |
| So that is the ... that's the ... I call
| | the strip is not wide enough to include everything |
| this ... can you see what I
| | from minus one to one. |
|
| |
|
| 0:10:42.240,0:10:43.040 | | 0:12:23.079,0:12:27.990 |
| call this?
| | Regardless of what Delta the prover picks, |
| | we know that however small an interval we |
|
| |
|
| 0:10:43.040,0:10:45.399 | | 0:12:27.990,0:12:32.180 |
| KM: The strongly telepathic prover.
| | pick around zero, the function is going to |
| | take all values from negative one to one in |
|
| |
|
| 0:10:45.399,0:10:51.470 | | 0:12:32.180,0:12:35.759 |
| Vipul: So, do you know what I meant by that?
| | that small interval. |
| Well, I meant the prover
| |
|
| |
|
| 0:10:51.470,0:10:58.470 | | 0:12:35.759,0:12:40.819 |
| is sort of reading the skeptic's mind. All
| | Now the skeptic will be able to find an x |
| right? It's called
| | such that the function value lies outside |
|
| |
|
| 0:11:07.769,0:11:10.329 | | 0:12:40.819,0:12:42.290 |
| telepathy.
| | the interval. |
|
| |
|
| 0:11:10.329,0:11:17.329 | | 0:12:42.290,0:12:45.579 |
| Okay, the next one.
| | The skeptic should...the key idea is that |
| | the skeptic pick epsilon small enough, in |
|
| |
|
| 0:11:25.589,0:11:30.230 | | 0:12:45.579,0:12:50.360 |
| This one says that the function defined this
| | this case the skeptic's choice of epsilon |
| way. Okay? It's defined
| | doesn't depend on what L the prover chose. |
|
| |
|
| 0:11:30.230,0:11:34.829 | | 0:12:50.360,0:12:51.269 |
| as g(x) is x when x is rational and zero when
| | It need not. |
| x is irrational. So,
| |
|
| |
|
| 0:11:34.829,0:11:41.829 | | 0:12:51.269,0:12:52.889 |
| what would this look like? Well, it's like
| | The strategy doesn't. |
| this. There's a line y
| |
|
| |
|
| 0:11:42.750,0:11:49.510 | | 0:12:52.889,0:12:59.889 |
| equals x and there's the x-axis and the
| | Then after the prover has picked a delta, |
| graph is just the irrational x
| | picked an x such that the function lies outside. |
|
| |
|
| 0:11:49.510,0:11:52.750 | | 0:13:01.249,0:13:07.410 |
| coordinate parts of this line and the rational
| | Regardless of the L the prover picks, |
| x coordinate parts of
| | that L doesn't work as a limit because |
|
| |
|
| 0:11:52.750,0:11:56.350 | | 0:13:07.410,0:13:10.550 |
| this line. It's kind of like both these
| | the skeptic wins and so the limit doesn't |
| lines but only parts of
| | exist.</toggledisplay> |
|
| |
|
| 0:11:56.350,0:11:58.529
| | ==Strategic aspects== |
| them. Right?
| |
|
| |
|
| 0:11:58.529,0:12:02.079
| | ===The strategy of small=== |
| Now we want to show that limit as x approaches
| |
| zero of g(x) is
| |
|
| |
|
| 0:12:02.079,0:12:06.899
| | In the game formulation of the limit, the following loose statements are true: |
| zero. So just in here, do you think the statement
| |
| is true? That x goes
| |
|
| |
|
| 0:12:06.899,0:12:09.910
| | * "Smaller is smarter" for the skeptic, i.e., the smaller the choice of <math>\varepsilon</math>, the better the outlook is for the skeptic to win. |
| to zero, does this function go to zero?
| | * "Smaller is smarter" for the prover, i.e., the smaller the choice of <math>\delta</math>, the better the outlook is for the prover to win. |
|
| |
|
| 0:12:09.910,0:12:10.610
| | In other words, each side benefits by making the crucial move of that side as small as possible. However, there does not exist any ''single'' arbitrarily small number -- this is related to the observation in the [[#Two key ideas|motivation section]] that there is no such thing as a ''single'' arbitrarily close number. Thus, saying "choose as small a value as possible" is not a coherent strategy. What we can say is the following: |
| KM: Yes.
| |
|
| |
|
| 0:12:10.610,0:12:17.610 | | * If a value of <math>\delta > 0</math> works for a given value of <math>\varepsilon > 0</math>, the same value of <math>\delta > 0</math> also works for larger choices of <math>\varepsilon</math>. |
| Vipul: Because both the pieces are going to
| | * If a value of <math>\delta > 0</math> works for a given value of <math>\varepsilon > 0</math>, smaller values of <math>\delta > 0</math> also work for the same choice of <math>\varepsilon</math>. |
| zero. That's the inclusion. Okay?
| |
|
| |
|
| 0:12:20.610,0:12:24.089
| | ===Prover's strategy revisited=== |
| This is the proof we have here. So the idea,
| |
| we again think about it
| |
|
| |
|
| 0:12:24.089,0:12:27.790
| | The prover, in choosing a winning strategy, must specify a rule that can determine a value of <math>\delta</math> that works in terms of the value of <math>\varepsilon</math> specified by the skeptic. In other words, the prover must have a way of specifying <math>\delta</math> ''as a function of'' <math>\varepsilon</math>. |
| in terms of the game. The skeptic first picks | |
| the epsilon, okay? Now | |
|
| |
|
| 0:12:27.790,0:12:30.779
| | The skeptic also chooses <math>x</math> in the next move. However, the prover has no way of knowing the value of <math>x</math> that the skeptic plans to pick. Thus, in order for the prover to have a winning strategy, the prover's choice of <math>\delta</math> should be such that ''no matter what'' <math>x</math> the skeptic picks, the prover wins. |
| that we would have to choose the delta, but
| |
| there are really two cases
| |
|
| |
|
| 0:12:30.779,0:12:35.200
| | ===Skeptic's strategy revisited=== |
| on x, right? x rational and x irrational.
| |
| So the prover chooses the
| |
|
| |
|
| 0:12:35.200,0:12:39.459
| | The skeptic, in choosing a winning strategy, must specify the value of <math>\varepsilon</math> and then specify how to pick a value of <math>x</math> that works. When picking the value of <math>\varepsilon</math>, the skeptic does not know what <math>\delta</math> the prover will pick. Thus, the skeptic's choice of <math>\varepsilon</math> cannot be dependent on the prover's subsequent choice of <math>\delta</math>. |
| delta based on sort of whether the x is rational
| |
| or irrational, so if
| |
|
| |
|
| 0:12:39.459,0:12:43.880
| | However, when picking the value of <math>x</math>, the skeptic is aware of (and constrained by) the prover's choice of <math>\delta</math>. |
| the x is rational then the prover just picks | |
| delta equals epsilon, and | |
|
| |
|
| 0:12:43.880,0:12:48.339
| | ==Misconceptions== |
| that's good enough for rational x, right?
| |
| Because for rational x the
| |
|
| |
|
| 0:12:48.339,0:12:51.410
| | Most misconceptions associated with the formal <math>\varepsilon-\delta</math> definition of limit have to do with the ordering of the moves in the game, who's in charge of what move, and what information each person has at the time of making the move. We describe some common misconceptions below. |
| slope of the line is one so picking delta
| |
| as epsilon is good enough.
| |
|
| |
|
| 0:12:51.410,0:12:55.760
| | <center>{{#widget:YouTube|id=F0r_offAc5M}}</center> |
| For irrational x, if the skeptic's planning
| |
| to choose an irrational x
| |
|
| |
|
| 0:12:55.760,0:12:59.730 | | Full timed transcript: <toggledisplay> |
| then the prover can just choose any delta
| | 0:00:15.500,0:00:19.140 |
| actually. Like just pick
| | Vipul: Okay. This talk is going to be about |
| | certain misconceptions |
|
| |
|
| 0:12:59.730,0:13:03.880 | | 0:00:19.140,0:00:22.440 |
| the delta in advance. Like delta is one or
| | that people have regarding limits and these |
| something. Because if x is
| | are misconceptions that |
|
| |
|
| 0:13:03.880,0:13:10.430 | | 0:00:22.440,0:00:25.840 |
| irrational then it's like a constant function
| | people generally acquire after... |
| and therefore, like, for
| |
|
| |
|
| 0:13:10.430,0:13:14.970 | | 0:00:25.840,0:00:29.180 |
| any delta the function is trapped within epsilon
| | These are not the misconceptions that |
| distance of the given
| | people have before studying limits, |
|
| |
|
| 0:13:14.970,0:13:16.970 | | 0:00:29.180,0:00:32.730 |
| limit. Okay?
| | these are misconceptions you might have after |
| | studying limits, |
|
| |
|
| 0:13:16.970,0:13:19.950 | | 0:00:32.730,0:00:35.059 |
| So the prover sort of makes two cases based
| | after studying the epsilon delta definition. |
| on whether the skeptic
| |
|
| |
|
| 0:13:19.950,0:13:26.950 | | 0:00:35.059,0:00:38.550 |
| will pick a rational or an irrational x and
| | I'm going to describe these misconceptions |
| sort of based on that if
| | in terms of the limit game, |
|
| |
|
| 0:13:27.040,0:13:30.730 | | 0:00:38.550,0:00:41.900 |
| it's rational this is the prover's strategy,
| | the prover skeptic game of the limit. Though |
| if it's irrational then
| | the misconceptions |
|
| |
|
| 0:13:30.730,0:13:34.050 | | 0:00:41.900,0:00:45.850 |
| the prover can just do any delta. | | themselves don't depend on |
| | the understanding of the |
|
| |
|
| 0:13:34.050,0:13:37.630 | | 0:00:45.850,0:00:49.059 |
| Can you tell me what's wrong with this proof?
| | game but to understand exactly what's |
| | happening, it's better to think |
|
| |
|
| 0:13:37.630,0:13:44.630 | | 0:00:49.059,0:00:51.010 |
| KM: So, you're still kind of basing it on
| | of it in terms of the game. |
| what the skeptic is going to
| |
|
| |
|
| 0:13:44.750,0:13:45.800 | | 0:00:51.010,0:00:55.370 |
| pick next.
| | First recall the definition. So limit as x |
| | approaches c of f(x) is a |
|
| |
|
| 0:13:45.800,0:13:49.100 | | 0:00:55.370,0:01:01.629 |
| Vipul: Okay. It's actually pretty much the
| | number L; so c and L are both numbers, real |
| same problem [as the
| | numbers. f is a function, |
|
| |
|
| 0:13:49.100,0:13:55.449 | | 0:01:01.629,0:01:06.380 |
| preceding one], in a somewhat minor form.
| | x is approaching c. And we said this is true |
| The prover is sort of making
| | if the following -- for |
|
| |
|
| 0:13:55.449,0:13:59.959 | | 0:01:06.380,0:01:10.180 |
| cases based on what the skeptic is going to
| | every epsilon greater than zero, there exists |
| do next, and choosing a
| | a delta greater than |
|
| |
|
| 0:13:59.959,0:14:01.940 | | 0:01:10.180,0:01:14.800 |
| strategy according to that. But the prover
| | zero such that for all x which are within delta |
| doesn't actually know what
| | distance of c, f(x) is |
|
| |
|
| 0:14:01.940,0:14:05.089 | | 0:01:14.800,0:01:17.590 |
| the skeptic is going to do next, so the prover
| | within epsilon distance of L. Okay? |
| should actually have a
| |
|
| |
|
| 0:14:05.089,0:14:08.970 | | 0:01:17.590,0:01:24.590 |
| single strategy that works in both cases.
| | Now, how do we describe this in terms for |
| If cases will be made to
| | limit game? |
|
| |
|
| 0:14:08.970,0:14:12.209 | | 0:01:26.530,0:01:33.530 |
| prove that the strategy works so the prover
| | KM: So, skeptic starts off with the first |
| has to have a single
| | part of the definition. |
|
| |
|
| 0:14:12.209,0:14:12.459 | | 0:01:34.990,0:01:38.189 |
| strategy.
| | Vipul: By picking the epsilon? Okay, that's |
| | the thing written in |
|
| |
|
| 0:14:12.449,0:14:15.370 | | 0:01:38.189,0:01:42.939 |
| Now in this case the strategy we can choose
| | black. What's the skeptic trying to do? What's the |
| the prover just, the | | goal of the skeptic? |
|
| |
|
| 0:14:15.370,0:14:18.779 | | 0:01:42.939,0:01:49.100 |
| prover can pick delta as epsilon because that
| | KM: To try and pick an epsilon that would |
| will work in both cases.
| | not work. |
|
| |
|
| 0:14:18.779,0:14:20.019 | | 0:01:49.100,0:01:53.450 |
| KM: Exactly.
| | Vipul: So the goal of the skeptic is to try |
| | to show that the statement is false. |
|
| |
|
| 0:14:20.019,0:14:23.320 | | 0:01:53.450,0:01:54.100 |
| Vipul: Yeah. But in general if you have two
| | KM: Yeah. |
| different piece
| |
|
| |
|
| 0:14:23.320,0:14:26.579 | | 0:01:54.100,0:01:57.790 |
| definitions then the way you would do it so
| | Vipul: Right? In this case the skeptic should |
| you would pick delta as
| | try to start by choosing |
|
| |
|
| 0:14:26.579,0:14:30.300 | | 0:01:57.790,0:02:02.220 |
| the min [minimum] of the delta that work in
| | an epsilon that is really [small] -- the goal of |
| the two different pieces, | | the skeptic is to pick an |
|
| |
|
| 0:14:30.300,0:14:32.910 | | 0:02:02.220,0:02:04.500 |
| because you sort of want to make sure that
| | epsilon that's really small, what is the |
| both cases are covered. But
| | skeptic trying to challenge |
|
| |
|
| 0:14:32.910,0:14:36.730 | | 0:02:04.500,0:02:07.920 |
| the point is you have to do that -- take | | the prover into doing by picking the epsilon? |
| the min use that rather than
| | The skeptic is trying to |
|
| |
|
| 0:14:36.730,0:14:39.730 | | 0:02:07.920,0:02:11.959 |
| just say, "I'm going to choose my delta
| | challenge the prover into trapping the function |
| based on what the skeptic is
| | close to L when x is |
|
| |
|
| 0:14:39.730,0:14:42.589 | | 0:02:11.959,0:02:17.040 |
| going to move next." Okay?
| | close to c. And the way the skeptic specifies |
| | what is meant by "close to L" is |
|
| |
|
| 0:14:42.589,0:14:49.120 | | 0:02:17.040,0:02:19.860 |
| This is a minor form of the same misconception
| | by the choice of epsilon. Okay? |
| that that was there in
| |
|
| |
|
| 0:14:49.120,0:14:56.120 | | 0:02:19.860,0:02:24.900 |
| the previous example we saw. | | When picking epsilon the skeptic is |
| | effectively picking this interval, L - |
|
| |
|
| 0:15:04.620,0:15:11.620 | | 0:02:24.900,0:02:30.700 |
| So, this is what I call the mildly telepathic
| | epsilon, L + epsilon). Okay? And basically |
| prover, right? The
| | that's what the skeptic is |
|
| |
|
| 0:15:14.970,0:15:18.579 | | 0:02:30.700,0:02:33.680 |
| prover is still behaving telepathically | | doing. The prover is then picking a delta. |
| predicting the skeptic's future
| | What is the goal of the |
|
| |
|
| 0:15:18.579,0:15:23.740 | | 0:02:33.680,0:02:36.239 |
| moves but it's not so bad. The prover is
| | prover in picking the delta? The prover is |
| just making, like, doing a
| | saying, "Here's how I can |
|
| |
|
| 0:15:23.740,0:15:25.470 | | 0:02:36.239,0:02:40.099 |
| coin toss type of telepathy. That isn't
| | trap the function within that interval. I'm |
| the only one the prover is
| | going to pick a delta and |
|
| |
|
| 0:15:25.470,0:15:30.790 | | 0:02:40.099,0:02:43.520 |
| actually, deciding exactly what x skeptic
| | my claim is that if the x value within delta distance of c, except the |
| would take. But it's still
| |
|
| |
|
| 0:15:30.790,0:15:32.790 | | 0:02:43.520,0:02:47.000 |
| the same problem and the reason why I think | | point c itself, so my claim is for any x value |
| people will have this
| | there the function is |
|
| |
|
| 0:15:32.790,0:15:36.329 | | 0:02:47.000,0:02:48.260 |
| misconception is because they don't think
| | trapped in here." |
| about it in terms of the
| |
|
| |
|
| 0:15:36.329,0:15:38.970 | | 0:02:48.260,0:02:52.819 |
| sequence in which the moves are made, and
| | So, the prover picks the delta and then the |
| the information that each
| | skeptic tries to |
|
| |
|
| 0:15:38.970,0:15:45.970 | | 0:02:52.819,0:02:56.709 |
| body has at any given stage of the game.
| | test the prover's claim by picking an x |
|
| |
|
| 0:15:50.889,0:15:57.889 | | 0:02:56.709,0:02:59.670 |
| Let's do this one.
| | which is within the interval specified by |
| | the prover and then they |
|
| |
|
| 0:16:10.930,0:16:15.259 | | 0:02:59.670,0:03:03.379 |
| So, this is a limit game, right? Let's say
| | both check whether f(x) is within epsilon |
| that limit as x approaches
| | distance [of L]. If it is |
|
| |
|
| 0:16:15.259,0:16:22.259 | | 0:03:03.379,0:03:07.940 |
| 1 of 2x is 2, okay? How do we go about showing
| | then the prover wins and if it is not, if |
| this? Well, the idea is | | this [|f(x) - L|]is not less |
|
| |
|
| 0:16:23.699,0:16:27.990 | | 0:03:07.940,0:03:09.989 |
| let's play the game, right? Let's say
| | than epsilon then the skeptic wins. Okay? |
| the skeptic it picks epsilon as
| |
|
| |
|
| 0:16:27.990,0:16:34.990 | | 0:03:09.989,0:03:13.659 |
| 0.1, okay? The prover picks delta as 0.05.
| | So, the skeptic is picking the neighborhood |
| The skeptic is then picking
| | of the target point which |
|
| |
|
| 0:16:35.139,0:16:38.790 | | 0:03:13.659,0:03:17.030 |
| epsilon as 0.1, the skeptic is saying, "Please | | in this case is just the open interval of |
| trap the function
| | radius epsilon, the prover |
|
| |
|
| 0:16:38.790,0:16:43.800 | | 0:03:17.030,0:03:21.940 |
| between 1.9 and 2.1. Okay? Find the delta
| | is picking the delta which is effectively the |
| small enough so that the
| | neighborhood of the domain |
|
| |
|
| 0:16:43.800,0:16:48.389 | | 0:03:21.940,0:03:25.760 |
| function value is dropped between 1.9 and
| | point except the point c as I've said open |
| 2.1. The prover picks delta
| | interval (c - delta, c + |
|
| |
|
| 0:16:48.389,0:16:55.389 | | 0:03:25.760,0:03:30.870 |
| as 0.05 which means the prover is now getting
| | delta) excluding c and then the skeptic picks |
| the input value trap | | an x in the neighborhood |
|
| |
|
| 0:16:57.850,0:17:04.850 | | 0:03:30.870,0:03:35.700 |
| between 0.95 and 1.05. That's 1 plus minus
| | specified by prover and if the function value |
| this thing. And now the
| | is within the interval |
|
| |
|
| 0:17:05.439,0:17:09.070 | | 0:03:35.700,0:03:38.830 |
| prover is claiming that if the x value is | | specified by the skeptic then the prover wins. |
| within this much distance of
| |
|
| |
|
| 0:17:09.070,0:17:13.959 | | 0:03:38.830,0:03:41.989 |
| 1 except the value equal to 1, then the function
| | Now, what does it mean to say the statement |
| value is within 0.1
| | is true in terms of the |
|
| |
|
| 0:17:13.959,0:17:17.630 | | 0:03:41.989,0:03:43.080 |
| distance of 2. So, the skeptic tries picking
| | game? |
| x within the interval
| |
|
| |
|
| 0:17:17.630,0:17:23.049 | | 0:03:43.080,0:03:50.080 |
| prescribed by the prover, so maybe the skeptic
| | KM: So, it means that the prover is always |
| picks 0.97 which is
| | going to win the game. |
|
| |
|
| 0:17:23.049,0:17:26.380 | | 0:03:51.849,0:03:55.629 |
| within 0.05 distance of 1.
| | Vipul: Well, sort of. I mean the prover may |
| | play it stupidly. The |
|
| |
|
| 0:17:26.380,0:17:31.570 | | 0:03:55.629,0:04:00.750 |
| And then they check that f(x) is 1.94, that
| | prover can win the game if the prover plays |
| is at the distance of 0.06
| | well. So, the prover has a |
|
| |
|
| 0:17:31.570,0:17:38.570 | | 0:04:00.750,0:04:03.230 |
| from 2. So, it's within 0.1 of the claimed
| | winning strategy for the game. Okay? |
| limit. Who won the game?
| |
|
| |
|
| 0:17:38.780,0:17:42.650 | | 0:04:05.230,0:04:10.299 |
| If the thing is within the interval then who
| | The statement is true if the prover has a |
| wins?
| | winning strategy for the |
|
| |
|
| 0:17:42.650,0:17:43.320 | | 0:04:10.299,0:04:14.090 |
| KM: The prover.
| | game and that means the prover has a way |
| | of playing the game such that |
|
| |
|
| 0:17:43.320,0:17:46.720 | | 0:04:14.090,0:04:17.320 |
| Vipul: The prover wins, right? So, the prover
| | whatever the skeptic does the prover is going |
| won again so therefore
| | to win the game. The |
|
| |
|
| 0:17:46.720,0:17:52.100 | | 0:04:17.320,0:04:20.789 |
| this limit statement is true, right? So, what's
| | statement is considered false if the skeptic |
| wrong with this as a
| | has a winning strategy |
|
| |
|
| 0:17:52.100,0:17:57.370 | | 0:04:20.789,0:04:23.370 |
| proof that the limit statement is true? How
| | for the game which means the skeptic has a |
| is this not a proof that
| | way of playing so that |
|
| |
|
| 0:17:57.370,0:18:03.870 | | 0:04:23.370,0:04:25.729 |
| the limit statement is true? This what I've | | whatever the prover does the skeptic can win |
| written here, why is that
| | the game. |
|
| |
|
| 0:18:03.870,0:18:05.990 | | 0:04:25.729,0:04:27.599 |
| not a proof that the limit statement is true?
| | Or if the game doesn't make sense at all |
| | ... |
|
| |
|
| 0:18:05.990,0:18:11.960 | | 0:04:27.599,0:04:29.460 |
| KM: Because it's only an example for the
| | maybe the function is not defined on |
| specific choice of epsilon and x.
| |
|
| |
|
| 0:18:11.960,0:18:16.200 | | 0:04:29.460,0:04:31.050 |
| Vipul: Yes, exactly. So, it's like a single
| | the immediate left and right of c. |
| play of the game, the
| |
|
| |
|
| 0:18:16.200,0:18:20.470 | | 0:04:31.050,0:04:32.370 |
| prover wins, but the limit statement doesn't
| | If the function isn't defined then we |
| just say that the prover
| |
|
| |
|
| 0:18:20.470,0:18:24.380 | | 0:04:32.370,0:04:34.160 |
| wins the game, it says the prover has a winning
| | cannot even make sense of the statement. |
| strategy. It says that
| |
|
| |
|
| 0:18:24.380,0:18:27.660 | | 0:04:34.160,0:04:36.990 |
| the prover can win the game regardless of
| | Either way -- the skeptic has a winning strategy |
| how the skeptic plays;
| |
|
| |
|
| 0:18:27.660,0:18:31.070 | | 0:04:36.990,0:04:37.770 |
| there's a way for the prover to do that.
| | or the game doesn't make sense -- |
| This just gives one example
| |
|
| |
|
| 0:18:31.070,0:18:34.640 | | 0:04:41.770,0:04:43.470 |
| where the prover won the game, but it doesn't
| | then the statement is false. |
| tell us that regardless
| |
|
| |
|
| 0:18:34.640,0:18:37.280 | | 0:04:43.470,0:04:47.660 |
| of the epsilon the skeptic takes the prover
| | If the prover has a winning strategy |
| can pick a delta such that
| | the statement is true. |
|
| |
|
| 0:18:37.280,0:18:41.090 | | 0:04:47.660,0:04:54.660 |
| regardless of the x the skeptic picks, the
| | With this background in mind let's look |
| function is within the
| | at some common misconceptions. |
|
| |
|
| 0:18:41.090,0:18:45.530 | | 0:04:56.540,0:05:03.540 |
| thing. So that's what they should do. Okay?
| | Okay. Let's say we are trying to prove that |
| | the limit as x approaches |
|
| |
|
| 0:18:45.530,0:18:51.160 | | 0:05:27.620,0:05:31.530 |
| Now you notice -- I'm sure you notice this
| | 2 of x^2 is 4, so is that statement correct? |
| but the way the game and the
| | The statement we're |
|
| |
|
| 0:18:51.160,0:18:58.160 | | 0:05:31.530,0:05:32.060 |
| limit definition. The way the limit definition
| | trying to prove? |
| goes, you see that all
| |
|
| |
|
| 0:18:59.870,0:19:04.260 | | 0:05:32.060,0:05:32.680 |
| the moves of the skeptic be right "for every"
| | KM: Yes. |
| "for all." Right? And
| |
|
| |
|
| 0:19:04.260,0:19:07.390 | | 0:05:32.680,0:05:35.960 |
| for all the moves of the prover it's "there
| | Vipul: That's correct. Because in fact x^2 |
| exists." Why do we do
| | is a continuous function |
|
| |
|
| 0:19:07.390,0:19:11.140 | | 0:05:35.960,0:05:40.160 |
| that? Because we are trying to get a winning
| | and the limit of a continuous function at |
| strategy for the prover,
| | the point is just the |
|
| |
|
| 0:19:11.140,0:19:14.309 | | 0:05:40.160,0:05:43.030 |
| so the prover controls his own moves. Okay?
| | value at the point and 2^2 is 4. But we're |
| | going to now try to prove |
|
| |
|
| 0:19:14.309,0:19:15.250 | | 0:05:43.030,0:05:48.530 |
| KM: Exactly.
| | this formally using the epsilon-delta definition |
| | of limit, okay? Now |
|
| |
|
| 0:19:15.250,0:19:18.630 | | 0:05:48.530,0:05:51.229 |
| Vipul: So, therefore wherever it's a prover
| | in terms of the epsilon-delta definition or |
| move it will be a there
| | rather in terms of this |
|
| |
|
| 0:19:18.630,0:19:22.240 | | 0:05:51.229,0:05:55.160 |
| exists. Where there is a skeptic's move
| | game setup, what we need to do is we need |
| the prover has to be prepared
| | to describe a winning |
|
| |
|
| 0:19:22.240,0:19:29.240 | | 0:05:55.160,0:06:01.460 |
| for anything the skeptic does. All those moves | | strategy for the prover. Okay? We need to |
| are "for every."
| | describe delta in terms of |
|
| |
|
| 0:19:30.559,0:19:33.850 | | 0:06:01.460,0:06:05.240 |
| One last one. By the way, this one was called,
| | epsilon. The prover essentially ... the only |
| "You say you want a
| | move the prover makes is |
|
| |
|
| 0:19:33.850,0:19:36.870 | | 0:06:05.240,0:06:09.130 |
| replay?" Which is basically they're just
| | this choice of delta. Right? The skeptic picked |
| saying that just one play is
| | epsilon, the prover |
|
| |
|
| 0:19:36.870,0:19:40.890 | | 0:06:09.130,0:06:12.810 |
| not good enough. If the statement is actually
| | picked delta then the skeptic picks x and |
| true, the prover should
| | then they judge who won. The |
|
| |
|
| 0:19:40.890,0:19:45.370 | | 0:06:12.810,0:06:15.810 |
| be willing to accept the skeptic ones, the
| | only choice the prover makes is the choice |
| reply and say they want to
| | of delta, right? |
|
| |
|
| 0:19:45.370,0:19:47.679 | | 0:06:15.810,0:06:16.979 |
| play it again, the prover should say "sure"
| | KM: Exactly. |
| and "I'm going to win
| |
|
| |
|
| 0:19:47.679,0:19:53.320 | | 0:06:16.979,0:06:20.080 |
| again." That's what it would mean for
| | Vipul: The prover has to specify delta in terms |
| the limit statement to be true.
| | of epsilon. |
|
| |
|
| 0:19:53.320,0:20:00.320 | | 0:06:20.080,0:06:24.819 |
| One last one. Just kind of pretty similar
| | So, here is my strategy. My strategy is I'm |
| to the one we just saw. Just | | going to choose delta as, |
|
| |
|
| 0:20:16.690,0:20:23.690 | | 0:06:24.819,0:06:29.509 |
| a little different. | | I as a prover is going to choose delta as |
| | epsilon over the absolute |
|
| |
|
| 0:20:39.020,0:20:46.020 | | 0:06:29.509,0:06:33.690 |
| Okay, this one, let's see. We are saying | | value of x plus 2 [|x + 2|]. Okay? |
| that the limit as x
| |
|
| |
|
| 0:20:50.450,0:20:56.900 | | 0:06:33.690,0:06:36.880 |
| approaches zero of sin(1/x) is zero, right?
| | Now, what I want to show that this strategy |
| Let's see how we prove
| | works. So, what I'm claiming |
|
| |
|
| 0:20:56.900,0:21:01.409 | | 0:06:36.880,0:06:39.840 |
| this. If the statement true ... well, do you
| | is that if ... so let me just finish this |
| think the statement is
| | and then you can tell me where |
|
| |
|
| 0:21:01.409,0:21:08.409 | | 0:06:39.840,0:06:43.419 |
| true? As x approach to zero, is sin 1 over
| | I went wrong here, okay? I'm claiming that |
| x approaching zero? So
| | this strategy works which |
|
| |
|
| 0:21:13.980,0:21:20.980 | | 0:06:43.419,0:06:47.130 |
| here's the picture of sin(1/x). y-axis.
| | means I'm claiming that if the skeptic now |
| It's an oscillatory function
| | picks any x which is within |
|
| |
|
| 0:21:22.010,0:21:27.870 | | 0:06:47.130,0:06:54.130 |
| and it has this kind of picture. Does it doesn't
| | delta distance of 2; the target point, |
| go to zero as x
| |
|
| |
|
| 0:21:27.870,0:21:29.270 | | 0:06:56.710,0:07:01.490 |
| approaches zero?
| | then the function value is within epsilon |
| | distance of 4, the claimed |
|
| |
|
| 0:21:29.270,0:21:30.669 | | 0:07:01.490,0:07:04.080 |
| KM: No.
| | limit. That's what I want to show. |
|
| |
|
| 0:21:30.669,0:21:35.539 | | 0:07:04.080,0:07:08.300 |
| Vipul: No. So, you said that this statement
| | Now is that true? Well, here's how I do |
| is false, but I'm going to
| | it. I say, I start by |
|
| |
|
| 0:21:35.539,0:21:38.700 | | 0:07:08.300,0:07:13.539 |
| try to show it's true. Here's how I do
| | taking this expression, I factor it as |
| that. Let's say the skeptic
| | |x - 2||x + 2|. The absolute |
|
| |
|
| 0:21:38.700,0:21:44.510 | | 0:07:13.539,0:07:16.810 |
| picks epsilon as two, okay? And then the prover
| | value of product is the product of the absolute |
| ... so, the epsilon is
| | values so this can be |
|
| |
|
| 0:21:44.510,0:21:48.520 | | 0:07:16.810,0:07:21.599 |
| two so that's the interval of width two
| | split like that. Now I say, well, we know |
| about the game limit zero. The
| | that |x - 2| is less than |
|
| |
|
| 0:21:48.520,0:21:55.150 | | 0:07:21.599,0:07:24.979 |
| prover picks delta as 1/pi. Whatever x the
| | delta and this is a positive thing. So we |
| skeptic picks, okay?
| | can write this as less than delta |
|
| |
|
| 0:21:55.150,0:22:02.150 | | 0:07:24.979,0:07:31.979 |
| Regardless of the x that the
| | times absolute value x plus 2. Right? And |
| skeptic picks, the function is trapped
| | this delta is epsilon over |
| within epsilon of the game limit. Is that
| |
|
| |
|
| 0:22:10.340,0:22:16.900 | | 0:07:35.599,0:07:37.620 |
| true? Yes, because sin
| | |x + 2| and we get epsilon. |
| (1/x) is between minus 1 and 1, right? Therefore
| |
|
| |
|
| 0:22:16.900,0:22:20.100 | | 0:07:37.620,0:07:40.460 |
| since the skeptic
| | So, this thing equals something, less than |
| picked an epsilon of 2, the function value
| | something, equals |
|
| |
|
| 0:22:20.100,0:22:24.030 | | 0:07:40.460,0:07:43.580 |
| is completely trapped in
| | something, equals something, you have a chain |
| the interval from -1 to 1, so therefore the
| | of things, there's one |
|
| |
|
| 0:22:24.030,0:22:27.919 | | 0:07:43.580,0:07:47.720 |
| prover managed to trap it
| | step that you have less than. So overall we |
| within distance of 2 of the claimed limit zero.
| | get that this expression, |
|
| |
|
| 0:22:27.919,0:22:30.970 | | 0:07:47.720,0:07:53.740 |
| Okay? Regardless of what
| | this thing is less than epsilon. So, we have |
| the skeptic does, right? It's not just saying | | shown that whatever x the |
|
| |
|
| 0:22:30.970,0:22:34.370 | | 0:07:53.740,0:08:00.370 |
| that the prover won the
| | skeptic would pick, the function value lies |
| game once, it's saying whatever x the skeptic
| | within the epsilon |
|
| |
|
| 0:22:34.370,0:22:40.740 | | 0:08:00.370,0:08:05.030 |
| picks the prover can
| | distance of the claimed limit. As long as the skeptic picks x within |
| still win the game. Right? Regardless if the
| |
|
| |
|
| 0:22:40.740,0:22:43.780 | | 0:08:05.030,0:08:09.240 |
| x is skeptic picks, the
| | delta distance of the target point. |
| prover picked a delta such that the function
| |
|
| |
|
| 0:22:43.780,0:22:48.100 | | 0:08:09.240,0:08:16.240 |
| is trapped. It's
| | Does this strategy work? Is this a proof? |
| completely trapped, okay? It's not an issue
| | What's wrong with this? |
|
| |
|
| 0:22:48.100,0:22:51.130 | | 0:08:24.270,0:08:31.270 |
| of whether the skeptic
| | Do you think there's anything wrong |
| picks the stupid x. Do you think that this
| | with the algebra I've done here? |
|
| |
|
| 0:22:51.130,0:22:52.130 | | 0:08:33.510,0:08:40.510 |
| proves the statement?
| | KM: Well, we said that ... |
|
| |
|
| 0:22:52.130,0:22:59.130 | | 0:08:40.910,0:08:47.910 |
| KM: No, I mean in this case it still depended
| | Vipul: So, is there anything wrong in the |
| on the epsilon that the
| | algebra here? This is this, |
|
| |
|
| 0:23:01.030,0:23:01.820 | | 0:08:50.160,0:08:51.740 |
| skeptic chose.
| | this is less than delta, delta ... So, this |
| | part |
|
| |
|
| 0:23:01.820,0:23:04.980 | | 0:08:51.740,0:08:52.089 |
| Vipul: It's still dependent on the epsilon
| | seems fine, right? |
| that the skeptic chose? So,
| |
|
| |
|
| 0:23:04.980,0:23:05.679 | | 0:08:52.089,0:08:52.339 |
| yes, that's exactly the problem.
| | KM: Yes. |
|
| |
|
| 0:23:05.679,0:23:09.370 | | 0:08:52.330,0:08:55.640 |
| So, we proved that the statement -- we prove | | Vipul: There's nothing wrong in the algebra |
| that from this part onward
| | here. So, what could be |
|
| |
|
| 0:23:09.370,0:23:12.500 | | 0:08:55.640,0:09:00.310 |
| but it still, we didn't prove it for all
| | wrong? Our setup seems fine. If the x value |
| epsilon, we only prove for
| | is within delta distance |
|
| |
|
| 0:23:12.500,0:23:16.309 | | 0:09:00.310,0:09:03.350 |
| epsilon is 2, and 2 is a very big number,
| | of 2 then the function value is within epsilon |
| right? Because the
| | distance of 4. That's |
|
| |
|
| 0:23:16.309,0:23:19.970 | | 0:09:03.350,0:09:05.360 |
| oscillation is all happening between minus
| | exactly what we want to prove, right? |
| 1 and 1, and if in fact the
| |
|
| |
|
| 0:23:19.970,0:23:26.970 | | 0:09:05.360,0:09:11.120 |
| skeptic had pick epsilon as 1 or something
| | So, there's nothing wrong this point onward. |
| smaller than 1 then the two
| | So, the error happened |
|
| |
|
| 0:23:27.030,0:23:32.169 | | 0:09:11.120,0:09:14.440 |
| epsilon strip width would not cover the entire
| | somewhere here. What do you think |
| -1, +1
| | was wrong |
|
| |
|
| 0:23:32.169,0:23:35.490 | | 0:09:14.440,0:09:21.160 |
| interval, and then whatever the prover did
| | here? In the strategy choice step? What do |
| the skeptic could actually | | you think went wrong in the |
|
| |
|
| 0:23:35.490,0:23:39.530 | | 0:09:21.160,0:09:24.010 |
| pick an x and show that it's not trapped.
| | strategy choice step? |
| So, in fact the reason why
| |
|
| |
|
| 0:23:39.530,0:23:43.110 | | 0:09:24.010,0:09:28.850 |
| the prover could win the game from this point
| | Well, okay, so in what order do they play their moves? |
| onward is that the
| | Skeptic will choose the epsilon, |
|
| |
|
| 0:23:43.110,0:23:45.900 | | 0:09:28.850,0:09:29.760 |
| skeptic made of stupid choice of epsilon.
| | then? |
| Okay?
| |
|
| |
|
| 0:23:45.900,0:23:52.289 | | 0:09:29.760,0:09:35.130 |
| In all these situation, all these misconceptions,
| | KM: Then the prover chooses delta. |
| the main problem is, | |
|
| |
|
| 0:23:52.289,0:23:58.919 | | 0:09:35.130,0:09:36.080 |
| that we're not ... keeping in mind the order
| | Vipul: Prover chooses delta. Then? |
| which the moves I made
| |
|
| |
|
| 0:23:58.919,0:24:04.179 | | 0:09:36.080,0:09:39.529 |
| and how much information each claim has at
| | KM: Then the skeptic has to choose the x value. |
| the stage where that move | |
|
| |
|
| 0:24:04.179,0:24:04.789 | | 0:09:39.529,0:09:42.470 |
| is being made.</toggledisplay> | | Vipul: x value. So, when the prover is deciding |
| | the strategy, when the |
|
| |
|
| ==Misconceptions==
| | 0:09:42.470,0:09:45.860 |
| | prover is choosing the delta, what information |
| | does the prover have? |
|
| |
|
| Most misconceptions associated with the formal <math>\varepsilon-\delta</math> definition of limit have to do with the ordering of the moves in the game, who's in charge of what move, and what information each person has at the time of making the move. We describe some common misconceptions below.
| | 0:09:45.860,0:09:48.410 |
| | KM: He just has the information on epsilon. |
|
| |
|
| <center>{{#widget:YouTube|id=Kms_VHwgdZ8}}</center>
| | 0:09:48.410,0:09:50.500 |
| | Vipul: Just the information on epsilon. So? |
|
| |
|
| Full timed transcript: <toggledisplay>
| | 0:09:50.500,0:09:57.060 |
| 0:00:15.500,0:00:19.140 | | KM: So, in this case the mistake was that |
| Vipul: Okay. This talk is going to be about
| | because he didn't know the x value yet? |
| certain misconceptions
| |
|
| |
|
| 0:00:19.140,0:00:22.440 | | 0:09:57.060,0:10:03.100 |
| that people have regarding limits and these
| | Vipul: The strategy cannot depend on x. |
| are misconceptions that
| |
|
| |
|
| 0:00:22.440,0:00:25.840 | | 0:10:03.100,0:10:04.800 |
| people generally acquire after...
| | KM: Yeah. |
|
| |
|
| 0:00:25.840,0:00:29.180 | | 0:10:04.800,0:10:09.790 |
| These are not the misconceptions that
| | Vipul: So, the prover is picking the |
| people have before studying limits,
| | delta based on x but the |
|
| |
|
| 0:00:29.180,0:00:32.730 | | 0:10:09.790,0:10:12.660 |
| these are misconceptions you might have after
| | prover doesn't know x at this stage when |
| studying limits,
| | picking the delta. The delta |
|
| |
|
| 0:00:32.730,0:00:35.059 | | 0:10:12.660,0:10:15.910 |
| after studying the epsilon delta definition.
| | that the prover chooses has to be completely |
| | a function of epsilon |
|
| |
|
| 0:00:35.059,0:00:38.550 | | 0:10:15.910,0:10:19.680 |
| I'm going to describe these misconceptions
| | alone, it cannot depend on the future moves |
| in terms of the limit game,
| | of the skeptic because the |
|
| |
|
| 0:00:38.550,0:00:41.900 | | 0:10:19.680,0:10:23.700 |
| the prover skeptic game of the limit. Though | | prover cannot read the skeptic's mind. Okay? |
| the misconceptions | | And doesn't know what the |
|
| |
|
| 0:00:41.900,0:00:45.850 | | 0:10:23.700,0:10:24.800 |
| themselves can be, sort of, don't depend
| | skeptic plans to do. |
| on the understanding of the
| |
|
| |
|
| 0:00:45.850,0:00:49.059 | | 0:10:24.800,0:10:31.800 |
| game but to understand exactly what's
| | So that is the ... that's the proof. I call |
| happening, it's better to think
| | this the ... |
|
| |
|
| 0:00:49.059,0:00:51.010 | | 0:10:42.240,0:10:43.040 |
| of it in terms of the game.
| | Can you see what I call this? |
|
| |
|
| 0:00:51.010,0:00:55.370 | | 0:10:43.040,0:10:45.399 |
| First recall the definition. So limit as x
| | KM: The strongly telepathic prover. |
| approaches c of f(x) is a
| |
|
| |
|
| 0:00:55.370,0:01:01.629 | | 0:10:45.399,0:10:51.470 |
| number L; so c and L are both numbers, real
| | Vipul: So, do you know what I meant by that? |
| numbers. f is a function,
| | Well, I meant the prover |
|
| |
|
| 0:01:01.629,0:01:06.380 | | 0:10:51.470,0:10:58.470 |
| x is approaching c. And we said this is true
| | is reading the skeptic's mind. All |
| if the following -- for
| | right? It's called telepathy. |
|
| |
|
| 0:01:06.380,0:01:10.180 | | 0:11:07.769,0:11:10.329 |
| every epsilon greater than zero, there exists
| |
| a delta greater than
| |
|
| |
|
| 0:01:10.180,0:01:14.800 | | 0:11:10.329,0:11:17.329 |
| zero such that for all x which are given delta
| | Okay, the next one. |
| distance of c, f(x) is
| |
|
| |
|
| 0:01:14.800,0:01:17.590 | | 0:11:25.589,0:11:30.230 |
| within epsilon distance of L. Okay?
| | This one says there's a function defined piecewise. Okay? It's defined |
|
| |
|
| 0:01:17.590,0:01:24.590 | | 0:11:30.230,0:11:34.829 |
| Now, how do we describe this in terms for
| | as g(x) is x when x is rational and zero when |
| limit game?
| | x is irrational. So, |
|
| |
|
| 0:01:26.530,0:01:33.530 | | 0:11:34.829,0:11:41.829 |
| KM: So, skeptic starts off with the first
| | what would this look like? Well, pictorially, there's a line y |
| part of the definition.
| |
|
| |
|
| 0:01:34.990,0:01:38.189 | | 0:11:42.750,0:11:49.510 |
| Vipul: By picking the epsilon? Okay, that's
| | equals x and there's the x-axis and the |
| the thing written in | | graph is just the irrational x |
|
| |
|
| 0:01:38.189,0:01:42.939 | | 0:11:49.510,0:11:52.750 |
| black. What's the skeptic trying to do? What's the
| | coordinate parts of this line and the rational |
| goal of the skeptic?
| | x coordinate parts of |
|
| |
|
| 0:01:42.939,0:01:49.100 | | 0:11:52.750,0:11:56.350 |
| KM: To try and pick an epsilon that would
| | this line. It's kind of like both these |
| not work.
| | lines but only parts of |
|
| |
|
| 0:01:49.100,0:01:53.450 | | 0:11:56.350,0:11:58.529 |
| Vipul: So the goal of the skeptic is to try
| | them. Right? |
| to show that the statement is false.
| |
|
| |
|
| 0:01:53.450,0:01:54.100 | | 0:11:58.529,0:12:02.079 |
| KM: Yeah.
| | Now we want to show that limit as x approaches |
| | zero of g(x) is |
|
| |
|
| 0:01:54.100,0:01:57.790 | | 0:12:02.079,0:12:06.899 |
| Vipul: Right? In this case the skeptic should
| | zero. So just intuitively, do you think the statement |
| try to start by choosing
| | is true? As x goes |
|
| |
|
| 0:01:57.790,0:02:02.220 | | 0:12:06.899,0:12:09.910 |
| an epsilon that is really -- the goal of
| | to zero, does this function go to zero? |
| the skeptic is to pick an
| |
|
| |
|
| 0:02:02.220,0:02:04.500 | | 0:12:09.910,0:12:10.610 |
| epsilon that's really small, what is the
| | KM: Yes. |
| skeptic trying to challenge
| |
|
| |
|
| 0:02:04.500,0:02:07.920 | | 0:12:10.610,0:12:17.610 |
| the prover into doing by picking the epsilon? | | Vipul: Because both the pieces are going to |
| The skeptic is trying to
| | zero. That's the intuition. Okay? |
|
| |
|
| 0:02:07.920,0:02:11.959 | | 0:12:20.610,0:12:24.089 |
| challenge the prover into trapping the function
| | This is the proof we have here. So the idea |
| close to L when x is
| | is we again think about it |
|
| |
|
| 0:02:11.959,0:02:17.040 | | 0:12:24.089,0:12:27.790 |
| close to c. And the skeptic specifies what
| | in terms of the game. The skeptic first picks |
| is meant by "close to L" is
| | the epsilon, okay? Now |
|
| |
|
| 0:02:17.040,0:02:19.860 | | 0:12:27.790,0:12:30.779 |
| by the choice of epsilon. Okay?
| | the prover has to choose the delta, but |
| | there are really two cases |
|
| |
|
| 0:02:19.860,0:02:24.900 | | 0:12:30.779,0:12:35.200 |
| When picking epsilon the skeptic is
| | on x, right? x rational and x irrational. |
| effectively picking this interval, L -
| | So the prover chooses the |
|
| |
|
| 0:02:24.900,0:02:30.700 | | 0:12:35.200,0:12:39.459 |
| epsilon, L + epsilon). Okay? And basically
| | delta based on whether the x is rational |
| that's what the skeptic is
| | or irrational, so if |
|
| |
|
| 0:02:30.700,0:02:33.680 | | 0:12:39.459,0:12:43.880 |
| doing. The prover is then picking a delta.
| | the x is rational then the prover just picks |
| What is the goal of the
| | delta equals epsilon, and |
|
| |
|
| 0:02:33.680,0:02:36.239 | | 0:12:43.880,0:12:48.339 |
| prover in picking the delta? The prover is
| | that's good enough for rational x, right? |
| saying, "Here's how I can
| | Because for rational x the |
|
| |
|
| 0:02:36.239,0:02:40.099 | | 0:12:48.339,0:12:51.410 |
| trap the function within that interval. I'm
| | slope of the line is one so picking delta |
| going to pick a delta and
| | as epsilon is good enough. |
|
| |
|
| 0:02:40.099,0:02:43.520 | | 0:12:51.410,0:12:55.760 |
| my claim is that if the x value within delta distance of c, except the
| | For irrational x, if the skeptic's planning |
| | to choose an irrational x |
|
| |
|
| 0:02:43.520,0:02:47.000 | | 0:12:55.760,0:12:59.730 |
| point c itself, so my claim is for any x value
| | then the prover can just choose any delta |
| there the function is
| | actually. Like just fix |
|
| |
|
| 0:02:47.000,0:02:48.260 | | 0:12:59.730,0:13:03.880 |
| trapped in here."
| | a delta in advance. Like delta is one or |
| | something. Because if x is |
|
| |
|
| 0:02:48.260,0:02:52.819 | | 0:13:03.880,0:13:10.430 |
| So, the prover picks the delta and then the
| | irrational then it's like a constant function |
| skeptic tries to meet the
| | and therefore, like, for |
|
| |
|
| 0:02:52.819,0:02:56.709 | | 0:13:10.430,0:13:14.970 |
| prover's claim or rather, test the prover's
| | any delta the function is trapped within epsilon |
| claim by picking an x
| | distance of the claimed |
|
| |
|
| 0:02:56.709,0:02:59.670 | | 0:13:14.970,0:13:16.970 |
| which is within the interval specified by
| | limit zero. Okay? |
| the prover and then they
| |
|
| |
|
| 0:02:59.670,0:03:03.379 | | 0:13:16.970,0:13:19.950 |
| both check whether f(x) is within epsilon
| | So the prover makes two cases based |
| distance [of L]. If it is
| | on whether the skeptic is going |
|
| |
|
| 0:03:03.379,0:03:07.940 | | 0:13:19.950,0:13:26.950 |
| then the prover wins and if it is not, if
| | to pick a rational or an irrational x |
| this [|f(x) - L|]is not less
| | and based on that if |
|
| |
|
| 0:03:07.940,0:03:09.989 | | 0:13:27.040,0:13:30.730 |
| than epsilon then the skeptic wins. Okay?
| | it's rational this is the prover's strategy, |
| | if it's irrational then |
|
| |
|
| 0:03:09.989,0:03:13.659 | | 0:13:30.730,0:13:34.050 |
| So, the skeptic is picking the neighborhood
| | the prover can just pick any delta. |
| of the target point which
| |
|
| |
|
| 0:03:13.659,0:03:17.030 | | 0:13:34.050,0:13:37.630 |
| in this case is just the open interval of
| | Can you tell me what's wrong with this proof? |
| radius epsilon, the prover
| |
|
| |
|
| 0:03:17.030,0:03:21.940 | | 0:13:37.630,0:13:44.630 |
| is picking the delta which is effectively the
| | KM: So, he [the prover] is still kind of |
| neighborhood of the domain
| | basing it on what the skeptic is going to |
|
| |
|
| 0:03:21.940,0:03:25.760 | | 0:13:44.750,0:13:45.800 |
| point except the point c as I've said open
| | pick next. |
| interval (c - delta, c +
| |
|
| |
|
| 0:03:25.760,0:03:30.870 | | 0:13:45.800,0:13:49.100 |
| delta) excluding c and then the skeptic picks
| | Vipul: Okay. It's actually pretty much the |
| an x in the neighborhood
| | same problem [as the |
|
| |
|
| 0:03:30.870,0:03:35.700 | | 0:13:49.100,0:13:55.449 |
| specified by prover and if the function value
| | preceding one], in a somewhat milder form. |
| is within the interval | | The prover is making |
|
| |
|
| 0:03:35.700,0:03:38.830 | | 0:13:55.449,0:13:59.959 |
| specified by the skeptic then the prover wins.
| | cases based on what the skeptic is going to |
| | do next, and choosing a |
|
| |
|
| 0:03:38.830,0:03:41.989 | | 0:13:59.959,0:14:01.940 |
| Now, what does it mean to say the statement
| | strategy according to that. But the prover |
| is true in terms of the
| | doesn't actually know what |
|
| |
|
| 0:03:41.989,0:03:43.080 | | 0:14:01.940,0:14:05.089 |
| game?
| | the skeptic is going to do next, so the prover |
| | should actually have a |
|
| |
|
| 0:03:43.080,0:03:50.080 | | 0:14:05.089,0:14:08.970 |
| KM: So, it means that the prover is always
| | single strategy that works in both cases. |
| going to win the game.
| | So cases will be made to |
|
| |
|
| 0:03:51.849,0:03:55.629 | | 0:14:08.970,0:14:12.209 |
| Vipul: Well, sort of. I mean the prover may
| | prove that the strategy works but the prover |
| play it stupidly. The
| | has to have a single |
|
| |
|
| 0:03:55.629,0:04:00.750 | | 0:14:12.209,0:14:12.459 |
| prover can win the game if the prover plays
| | strategy. |
| well. So, the prover has a
| |
|
| |
|
| 0:04:00.750,0:04:03.230 | | 0:14:12.449,0:14:15.370 |
| winning strategy for the game. Okay?
| | Now in this case the correct way of doing the proof is just, the |
|
| |
|
| 0:04:05.230,0:04:10.299 | | 0:14:15.370,0:14:18.779 |
| The statement is true if the prover has a
| | prover can pick delta as epsilon because that |
| winning strategy for [the
| | will work in both cases. |
|
| |
|
| 0:04:10.299,0:04:14.090 | | 0:14:18.779,0:14:20.019 |
| game] and that means the prover has a way
| | KM: Exactly. |
| of playing the game such that
| |
|
| |
|
| 0:04:14.090,0:04:17.320 | | 0:14:20.019,0:14:23.320 |
| whatever the skeptic does the prover is going
| | Vipul: Yeah. But in general if you have two |
| to win the game. The
| | different piece |
|
| |
|
| 0:04:17.320,0:04:20.789 | | 0:14:23.320,0:14:26.579 |
| statement is considered false if the skeptic
| | definitions then the way you would do it so |
| has a winning strategy
| | you would pick delta as |
|
| |
|
| 0:04:20.789,0:04:23.370 | | 0:14:26.579,0:14:30.300 |
| for the game which means the skeptic has a
| | the min [minimum] of the deltas that work in |
| way of playing so that
| | the two different pieces, |
|
| |
|
| 0:04:23.370,0:04:25.729 | | 0:14:30.300,0:14:32.910 |
| whatever the prover does the skeptic can win
| | because you want to make sure that |
| the game.
| | both cases are covered. But |
|
| |
|
| 0:04:25.729,0:04:27.599 | | 0:14:32.910,0:14:36.730 |
| Or if the game doesn't make sense at all
| | the point is you have to do that -- take |
| ...
| | the min use that rather than |
|
| |
|
| 0:04:27.599,0:04:29.460 | | 0:14:36.730,0:14:39.730 |
| maybe the function is not defined on
| | just say, "I'm going to choose my delta |
| | based on what the skeptic is |
|
| |
|
| 0:04:29.460,0:04:31.050 | | 0:14:39.730,0:14:42.589 |
| the immediate left and right of c.
| | going to move next." Okay? |
|
| |
|
| 0:04:31.050,0:04:32.370 | | 0:14:42.589,0:14:49.120 |
| If the function isn't defined then we
| | So this is a milder form of the same |
| | misconception that that was there in |
|
| |
|
| 0:04:32.370,0:04:34.160 | | 0:14:49.120,0:14:56.120 |
| cannot even make sense of the statement.
| | the previous example we saw. |
|
| |
|
| 0:04:34.160,0:04:36.990 | | 0:15:04.620,0:15:11.620 |
| Either way -- the skeptic has a winning strategy
| | So, this is what I call the mildly telepathic |
| | prover, right? The |
|
| |
|
| 0:04:36.990,0:04:37.770 | | 0:15:14.970,0:15:18.579 |
| or the game doesn't make sense --
| | prover is still behaving telepathically |
| | predicting the skeptic's future |
|
| |
|
| 0:04:41.770,0:04:43.470 | | 0:15:18.579,0:15:23.740 |
| then the statement is false.
| | moves but it's not so bad. The prover is |
| | just making, like, doing a |
|
| |
|
| 0:04:43.470,0:04:47.660 | | 0:15:23.740,0:15:25.470 |
| If the prover has a winning strategy
| | coin toss type of telepathy. Whereas in the |
| the statement is true.
| | earlier one is prover is |
|
| |
|
| 0:04:47.660,0:04:54.660 | | 0:15:25.470,0:15:30.790 |
| With this background in mind let's look
| | actually, deciding exactly what x the skeptic |
| at some common misconceptions.
| | would pick. But it's still |
|
| |
|
| 0:04:56.540,0:05:03.540 | | 0:15:30.790,0:15:32.790 |
| Okay. Let's say we are trying to prove that
| | the same problem and the reason why I think |
| the limit as x approaches
| | people will have this |
|
| |
|
| 0:05:27.620,0:05:31.530 | | 0:15:32.790,0:15:36.329 |
| 2 of x^2 is 4, so is that statement correct?
| | misconception is because they don't think |
| The statement we're
| | about it in terms of the |
|
| |
|
| 0:05:31.530,0:05:32.060 | | 0:15:36.329,0:15:38.970 |
| trying to prove?
| | sequence in which the moves are made, and |
| | the information that each |
|
| |
|
| 0:05:32.060,0:05:32.680 | | 0:15:38.970,0:15:45.970 |
| KM: Yes.
| | party has at any given stage of the game. |
|
| |
|
| 0:05:32.680,0:05:35.960 | | 0:15:50.889,0:15:57.889 |
| Vipul: That's correct. Because in fact x^2
| | Let's do this one. |
| is a continuous function
| |
|
| |
|
| 0:05:35.960,0:05:40.160 | | 0:16:10.930,0:16:15.259 |
| and the limit of a continuous function at
| | So, this is a limit claim, right? It says |
| the point is just the | | that the limit as x approaches |
|
| |
|
| 0:05:40.160,0:05:43.030 | | 0:16:15.259,0:16:22.259 |
| value at the point and 2^2 is 4. But we're
| | 1 of 2x is 2, okay? How do we go about showing |
| going to now try to prove
| | this? Well, the idea is |
|
| |
|
| 0:05:43.030,0:05:48.530 | | 0:16:23.699,0:16:27.990 |
| this formally using the epsilon-delta definition
| | let's play the game, right? Let's say |
| of limit, okay? Now
| | the skeptic picks epsilon as |
|
| |
|
| 0:05:48.530,0:05:51.229 | | 0:16:27.990,0:16:34.990 |
| in terms of the epsilon-delta definition or
| | 0.1, okay? The prover picks delta as 0.05. |
| rather in terms of this
| | The skeptic is when picking |
|
| |
|
| 0:05:51.229,0:05:55.160 | | 0:16:35.139,0:16:38.790 |
| game setup, what we need to do is we need
| | epsilon as 0.1, the skeptic is saying, "Please |
| to describe a winning
| | trap the function |
|
| |
|
| 0:05:55.160,0:06:01.460 | | 0:16:38.790,0:16:43.800 |
| strategy for the prover. Okay? We need to
| | between 1.9 and 2.1. Okay? Find the delta |
| describe delta in terms of
| | small enough so that the |
|
| |
|
| 0:06:01.460,0:06:05.240 | | 0:16:43.800,0:16:48.389 |
| epsilon. The prover essentially ... the only
| | function value is trapped between 1.9 and |
| move the prover makes is
| | 2.1. The prover picks delta |
|
| |
|
| 0:06:05.240,0:06:09.130 | | 0:16:48.389,0:16:55.389 |
| this choice of delta. Right? The skeptic picked
| | as 0.05 which means the prover is now getting |
| epsilon, the prover
| | the input value trapped |
|
| |
|
| 0:06:09.130,0:06:12.810 | | 0:16:57.850,0:17:04.850 |
| picked delta then the skeptic picks x and
| | between 0.95 and 1.05. That's 1 plus minus |
| then they judge who won. The
| | this thing. And now the |
|
| |
|
| 0:06:12.810,0:06:15.810 | | 0:17:05.439,0:17:09.070 |
| only choice the prover makes is the choice
| | prover is claiming that if the x value is |
| of delta, right? | | within this much distance of |
|
| |
|
| 0:06:15.810,0:06:16.979 | | 0:17:09.070,0:17:13.959 |
| KM: Exactly.
| | 1 except the value equal to 1, then the function |
| | value is within 0.1 |
|
| |
|
| 0:06:16.979,0:06:20.080 | | 0:17:13.959,0:17:17.630 |
| Vipul: The prover chooses the delta in terms
| | distance of 2. So, the skeptic tries picking |
| of epsilon.
| | x within the interval |
|
| |
|
| 0:06:20.080,0:06:24.819 | | 0:17:17.630,0:17:23.049 |
| So, here is my strategy. My strategy is I'm
| | specified by the prover, so maybe the skeptic |
| going to choose delta as,
| | picks 0.97 which is |
|
| |
|
| 0:06:24.819,0:06:29.509 | | 0:17:23.049,0:17:26.380 |
| I as a prover is going to choose delta as
| | within 0.05 distance of 1. |
| epsilon over the absolute
| |
|
| |
|
| 0:06:29.509,0:06:33.690 | | 0:17:26.380,0:17:31.570 |
| value of x plus 2 [|x + 2|]. Okay?
| | And then they check that 2x [the function f(x)] is |
| | 1.94, that is at the distance of 0.06 |
|
| |
|
| 0:06:33.690,0:06:36.880 | | 0:17:31.570,0:17:38.570 |
| Now, what I want to show that this strategy
| | from 2. So, it's within 0.1 of the claimed |
| works. So, what I'm aiming
| | limit 2. So who won the game? |
|
| |
|
| 0:06:36.880,0:06:39.840 | | 0:17:38.780,0:17:42.650 |
| is that if ... so let me just finish this | | If the thing is within the interval then who |
| and then you can tell me where
| | wins? |
|
| |
|
| 0:06:39.840,0:06:43.419 | | 0:17:42.650,0:17:43.320 |
| I went wrong here, okay? I'm claiming that
| | KM: The prover. |
| this strategy works which
| |
|
| |
|
| 0:06:43.419,0:06:47.130 | | 0:17:43.320,0:17:46.720 |
| means I'm claiming that if the skeptic now
| | Vipul: The prover wins, right? So, the prover |
| picks any x which is within
| | won the game so therefore |
|
| |
|
| 0:06:47.130,0:06:54.130 | | 0:17:46.720,0:17:52.100 |
| delta distance of 2; the target point,
| | this limit statement is true, right? So, what's |
| | wrong with this as a |
|
| |
|
| 0:06:56.710,0:07:01.490 | | 0:17:52.100,0:17:57.370 |
| then the function value is within epsilon
| | proof that the limit statement is true? How |
| distance of 4, the claimed
| | is this not a proof that |
|
| |
|
| 0:07:01.490,0:07:04.080 | | 0:17:57.370,0:18:03.870 |
| limit. That's what I want to show. | | the limit statement is true? This what I've |
| | written here, why is that |
|
| |
|
| 0:07:04.080,0:07:08.300 | | 0:18:03.870,0:18:05.990 |
| Now is that true? Well, here's how I do
| | not a proof that the limit statement is true? |
| it. I think, I started by
| |
|
| |
|
| 0:07:08.300,0:07:13.539 | | 0:18:05.990,0:18:11.960 |
| picking this expression, I factored it as
| | KM: Because it's only an example for the |
| |x - 2||x + 2|. The absolute
| | specific choice of epsilon and x. |
|
| |
|
| 0:07:13.539,0:07:16.810 | | 0:18:11.960,0:18:16.200 |
| value of product is the product of the absolute
| | Vipul: Yes, exactly. So, it's like a single |
| values so this can be
| | play of the game, the |
|
| |
|
| 0:07:16.810,0:07:21.599 | | 0:18:16.200,0:18:20.470 |
| split like that. Now I see, while we know
| | prover wins, but the limit statement doesn't |
| that |x - 2| is less than | | just say that the prover |
|
| |
|
| 0:07:21.599,0:07:24.979 | | 0:18:20.470,0:18:24.380 |
| delta and this is a positive thing. So we
| | wins the game, it says the prover has a winning |
| can either less than delta
| | strategy. It says that |
|
| |
|
| 0:07:24.979,0:07:31.979 | | 0:18:24.380,0:18:27.660 |
| times absolute value x plus 2. Right? And
| | the prover can win the game regardless of |
| this delta is epsilon over
| | how the skeptic plays; |
|
| |
|
| 0:07:35.599,0:07:37.620 | | 0:18:27.660,0:18:31.070 |
| |x + 2| and we get epsilon.
| | there's a way for the prover to do that. |
| | This just gives one example |
|
| |
|
| 0:07:37.620,0:07:40.460 | | 0:18:31.070,0:18:34.640 |
| So, this thing equals something, less than
| | where the prover won the game, but it doesn't |
| something, equals
| | tell us that regardless |
|
| |
|
| 0:07:40.460,0:07:43.580 | | 0:18:34.640,0:18:37.280 |
| something, equals something, you have a chain
| | of the epsilon the skeptic picks the prover |
| of things, there's one
| | can pick a delta such that |
|
| |
|
| 0:07:43.580,0:07:47.720 | | 0:18:37.280,0:18:41.090 |
| step that you have less than. So overall we
| | regardless of the x the skeptic picks, the |
| get that this expression,
| | function is within the |
|
| |
|
| 0:07:47.720,0:07:53.740 | | 0:18:41.090,0:18:45.530 |
| this thing is less than epsilon. So, we have
| | thing. So that's the issue here. Okay? |
| shown that whatever x the
| |
|
| |
|
| 0:07:53.740,0:08:00.370 | | 0:18:45.530,0:18:51.160 |
| skeptic would pick, the function value lies
| | Now you notice -- I'm sure you've noticed |
| within the epsilon
| | this but the way the game and the |
|
| |
|
| 0:08:00.370,0:08:05.030 | | 0:18:51.160,0:18:58.160 |
| distance of the claimed limit. Whatever the
| | limit definition. The way the limit definition |
| skeptic picks (x within the
| | goes, you see that all |
|
| |
|
| 0:08:05.030,0:08:09.240 | | 0:18:59.870,0:19:04.260 |
| delta distance of the target point).
| | the moves of the skeptic we write "for every" |
| | "for all." Right? And |
|
| |
|
| 0:08:09.240,0:08:16.240 | | 0:19:04.260,0:19:07.390 |
| Does this strategy work? Is this a proof?
| | for all the moves of the prover we write "there |
| What's wrong with this?
| | exists." Why do we do |
|
| |
|
| 0:08:24.270,0:08:31.270 | | 0:19:07.390,0:19:11.140 |
| Do you think there's anything wrong
| | that? Because we are trying to get a winning |
| with the algebra down here?
| | strategy for the prover, |
|
| |
|
| 0:08:33.510,0:08:40.510 | | 0:19:11.140,0:19:14.309 |
| KM: Well, we said that ...
| | so the prover controls his own moves. Okay? |
|
| |
|
| 0:08:40.910,0:08:47.910 | | 0:19:14.309,0:19:15.250 |
| Vipul: So, is there anything wrong in the
| | KM: Exactly. |
| algebra here? This is this,
| |
|
| |
|
| 0:08:50.160,0:08:51.740 | | 0:19:15.250,0:19:18.630 |
| this is less than delta, delta ... So, this
| | Vipul: So, therefore wherever it's a prover |
| part
| | move it will be a there |
|
| |
|
| 0:08:51.740,0:08:52.089 | | 0:19:18.630,0:19:22.240 |
| seems fine, right?
| | exists. Where there is a skeptic's move |
| | the prover has to be prepared |
|
| |
|
| 0:08:52.089,0:08:52.339 | | 0:19:22.240,0:19:29.240 |
| KM: Yes.
| | for anything the skeptic does. All those moves |
| | are "for every." |
|
| |
|
| 0:08:52.330,0:08:55.640 | | 0:19:30.559,0:19:33.850 |
| Vipul: There's nothing wrong in the algebra
| | One last one. By the way, this one was called, |
| here. So, what could be
| | "You say you want a |
|
| |
|
| 0:08:55.640,0:09:00.310 | | 0:19:33.850,0:19:36.870 |
| wrong? Our setup seems fine. If the x value
| | replay?" Which is basically they're just |
| is within delta distance | | saying that just one play is |
|
| |
|
| 0:09:00.310,0:09:03.350 | | 0:19:36.870,0:19:40.890 |
| of 2 then the function value is within epsilon
| | not good enough. If the statement is actually |
| this is 4. That's
| | true, the prover should |
|
| |
|
| 0:09:03.350,0:09:05.360 | | 0:19:40.890,0:19:45.370 |
| exactly what we want to prove, correct?
| | be willing to accept it if the skeptic wants a |
| | replay and say they want to |
|
| |
|
| 0:09:05.360,0:09:11.120 | | 0:19:45.370,0:19:47.679 |
| So, there's nothing wrong this point onward.
| | play it again, the prover should say "sure" |
| So, the error happened
| | and "I'm going to win |
|
| |
|
| 0:09:11.120,0:09:14.440 | | 0:19:47.679,0:19:53.320 |
| somewhere here. Where do you think that part
| | again." That's what it would mean for |
| you think what is wrong
| | the limit statement to be true. |
|
| |
|
| 0:09:14.440,0:09:21.160 | | 0:19:53.320,0:20:00.320 |
| here? In the strategy choice step? What do
| | One last one. Just kind of pretty similar |
| you think went wrong in the
| | to the one we just saw. But with |
|
| |
|
| 0:09:21.160,0:09:24.010 | | 0:20:16.690,0:20:23.690 |
| strategy choice step?
| | a little twist. |
|
| |
|
| 0:09:24.010,0:09:28.850 | | 0:20:39.020,0:20:46.020 |
| What? Okay, so let's go over the game. Skeptic
| | Okay, this one, let's see. We are saying |
| will choose the epsilon,
| | that the limit as x |
|
| |
|
| 0:09:28.850,0:09:29.760 | | 0:20:50.450,0:20:56.900 |
| then?
| | approaches zero of sin(1/x) is zero, right? |
| | Let's see how we prove |
|
| |
|
| 0:09:29.760,0:09:35.130 | | 0:20:56.900,0:21:01.409 |
| KM: Then the prover chooses delta.
| | this. If the statement true ... well, do you |
| | think the statement is |
|
| |
|
| 0:09:35.130,0:09:36.080 | | 0:21:01.409,0:21:08.409 |
| Vipul: Prover chooses delta. Then?
| | true? As x approach to zero, is sin 1 over |
| | x approaching zero? So |
|
| |
|
| 0:09:36.080,0:09:39.529 | | 0:21:13.980,0:21:20.980 |
| KM: Then the skeptic has to choose the x value.
| | here's the picture of sin(1/x). y-axis. |
| | It's an oscillatory function |
|
| |
|
| 0:09:39.529,0:09:42.470 | | 0:21:22.010,0:21:27.870 |
| Vipul: x value. So, when the prover is deciding
| | and it has this kind of picture. Does it doesn't |
| the strategy, when the
| | go to zero as x |
|
| |
|
| 0:09:42.470,0:09:45.860 | | 0:21:27.870,0:21:29.270 |
| prover is choosing the delta, what information
| | approaches zero? |
| does the prover have?
| |
|
| |
|
| 0:09:45.860,0:09:48.410 | | 0:21:29.270,0:21:30.669 |
| KM: He just has the information epsilon. | | KM: No. |
|
| |
|
| 0:09:48.410,0:09:50.500 | | 0:21:30.669,0:21:35.539 |
| Vipul: Just the information on epsilon. So? | | Vipul: No. So, you said that this statement |
| | is false, but I'm going to |
|
| |
|
| 0:09:50.500,0:09:57.060 | | 0:21:35.539,0:21:38.700 |
| KM: So, in this case the mistake was that
| | try to show it's true. Here's how I do |
| because he didn't know the x value yet?
| | that. Let's say the skeptic |
|
| |
|
| 0:09:57.060,0:10:03.100 | | 0:21:38.700,0:21:44.510 |
| Vipul: The strategy cannot depend on x.
| | picks epsilon as two, okay? And then the prover |
| | ... so, the epsilon is |
|
| |
|
| 0:10:03.100,0:10:04.800 | | 0:21:44.510,0:21:48.520 |
| KM: Yeah.
| | two so that's the interval of width two |
| | about the game limit zero. The |
|
| |
|
| 0:10:04.800,0:10:09.790 | | 0:21:48.520,0:21:55.150 |
| Vipul: So, the prover is sort of picking the
| | prover picks delta as 1/pi. Whatever x the |
| delta based on x but the | | skeptic picks, okay? |
|
| |
|
| 0:10:09.790,0:10:12.660 | | 0:21:55.150,0:22:02.150 |
| prover doesn't know x at this stage when
| | Regardless of the x that the |
| picking the delta. The delta
| | skeptic picks, the function is trapped |
| | within epsilon of the game limit. Is that |
|
| |
|
| 0:10:12.660,0:10:15.910 | | 0:22:10.340,0:22:16.900 |
| that the prover chooses has to be completely
| | true? Yes, because sin |
| a function of epsilon
| | (1/x) is between minus 1 and 1, right? Therefore |
|
| |
|
| 0:10:15.910,0:10:19.680 | | 0:22:16.900,0:22:20.100 |
| alone, it cannot depend on the future moves
| | since the skeptic |
| of the skeptic because the | | picked an epsilon of 2, the function value |
|
| |
|
| 0:10:19.680,0:10:23.700 | | 0:22:20.100,0:22:24.030 |
| prover cannot read the skeptic's mind. Okay?
| | is completely trapped in |
| And doesn't know what the
| | the interval from -1 to 1, so therefore the |
|
| |
|
| 0:10:23.700,0:10:24.800 | | 0:22:24.030,0:22:27.919 |
| skeptic plans to do.
| | prover managed to trap it |
| | within distance of 2 of the claimed limit zero. |
|
| |
|
| 0:10:24.800,0:10:31.800 | | 0:22:27.919,0:22:30.970 |
| So that is the ... that's the ... I call
| | Okay? Regardless of what |
| this ... can you see what I
| | the skeptic does, right? It's not just saying |
|
| |
|
| 0:10:42.240,0:10:43.040 | | 0:22:30.970,0:22:34.370 |
| call this?
| | that the prover won the |
| | game once, it's saying whatever x the skeptic |
|
| |
|
| 0:10:43.040,0:10:45.399 | | 0:22:34.370,0:22:40.740 |
| KM: The strongly telepathic prover.
| | picks the prover can |
| | still win the game. Right? Regardless if the |
|
| |
|
| 0:10:45.399,0:10:51.470 | | 0:22:40.740,0:22:43.780 |
| Vipul: So, do you know what I meant by that?
| | x the skeptic picks, the |
| Well, I meant the prover
| | prover picked a delta such that the function |
|
| |
|
| 0:10:51.470,0:10:58.470 | | 0:22:43.780,0:22:48.100 |
| is sort of reading the skeptic's mind. All | | is trapped. It's |
| right? It's called
| | completely trapped, okay? It's not an issue |
|
| |
|
| 0:11:07.769,0:11:10.329 | | 0:22:48.100,0:22:51.130 |
| telepathy.
| | of whether the skeptic |
| | picked a stupid x. Do you think that this |
|
| |
|
| 0:11:10.329,0:11:17.329 | | 0:22:51.130,0:22:52.130 |
| Okay, the next one.
| | proves the statement? |
|
| |
|
| 0:11:25.589,0:11:30.230 | | 0:22:52.130,0:22:59.130 |
| This one says that the function defined this
| | KM: No, I mean in this case it still depended |
| way. Okay? It's defined
| | on the epsilon that the |
|
| |
|
| 0:11:30.230,0:11:34.829 | | 0:23:01.030,0:23:01.820 |
| as g(x) is x when x is rational and zero when
| | skeptic chose. |
| x is irrational. So,
| |
|
| |
|
| 0:11:34.829,0:11:41.829 | | 0:23:01.820,0:23:04.980 |
| what would this look like? Well, it's like
| | Vipul: It's still dependent on the epsilon |
| this. There's a line y
| | that the skeptic chose? So, |
|
| |
|
| 0:11:42.750,0:11:49.510 | | 0:23:04.980,0:23:05.679 |
| equals x and there's the x-axis and the
| | yes, that's exactly the problem. |
| graph is just the irrational x
| |
|
| |
|
| 0:11:49.510,0:11:52.750 | | 0:23:05.679,0:23:09.370 |
| coordinate parts of this line and the rational
| | So, we proved that the statement -- we prove |
| x coordinate parts of
| | that from this part onward |
|
| |
|
| 0:11:52.750,0:11:56.350 | | 0:23:09.370,0:23:12.500 |
| this line. It's kind of like both these
| | but it still, we didn't prove it for all |
| lines but only parts of
| | epsilon, we only prove for |
|
| |
|
| 0:11:56.350,0:11:58.529 | | 0:23:12.500,0:23:16.309 |
| them. Right?
| | epsilon is 2, and 2 is a very big number, |
| | right? Because the |
|
| |
|
| 0:11:58.529,0:12:02.079 | | 0:23:16.309,0:23:19.970 |
| Now we want to show that limit as x approaches
| | oscillation is all happening between minus |
| zero of g(x) is
| | 1 and 1, and if in fact the |
|
| |
|
| 0:12:02.079,0:12:06.899 | | 0:23:19.970,0:23:26.970 |
| zero. So just in here, do you think the statement
| | skeptic had pick epsilon as 1 or something |
| is true? That x goes
| | smaller than 1 then the two |
|
| |
|
| 0:12:06.899,0:12:09.910 | | 0:23:27.030,0:23:32.169 |
| to zero, does this function go to zero?
| | epsilon strip width would not cover the entire |
| | -1, +1 |
|
| |
|
| 0:12:09.910,0:12:10.610 | | 0:23:32.169,0:23:35.490 |
| KM: Yes.
| | interval, and then whatever the prover did |
| | the skeptic could actually |
|
| |
|
| 0:12:10.610,0:12:17.610 | | 0:23:35.490,0:23:39.530 |
| Vipul: Because both the pieces are going to
| | pick an x and show that it's not trapped. |
| zero. That's the inclusion. Okay?
| | So, in fact the reason why |
|
| |
|
| 0:12:20.610,0:12:24.089 | | 0:23:39.530,0:23:43.110 |
| This is the proof we have here. So the idea,
| | the prover could win the game from this point |
| we again think about it
| | onward is that the |
|
| |
|
| 0:12:24.089,0:12:27.790 | | 0:23:43.110,0:23:45.900 |
| in terms of the game. The skeptic first picks
| | skeptic made a stupid choice of epsilon. |
| the epsilon, okay? Now
| | Okay? |
|
| |
|
| 0:12:27.790,0:12:30.779 | | 0:23:45.900,0:23:52.289 |
| that we would have to choose the delta, but
| | In all these situation, all these misconceptions, |
| there are really two cases
| | the main problem is, |
|
| |
|
| 0:12:30.779,0:12:35.200 | | 0:23:52.289,0:23:58.919 |
| on x, right? x rational and x irrational.
| | that we're not ... keeping in mind the order |
| So the prover chooses the
| | which the moves I made |
|
| |
|
| 0:12:35.200,0:12:39.459 | | 0:23:58.919,0:24:04.179 |
| delta based on sort of whether the x is rational
| | and how much information each claim has at |
| or irrational, so if
| | the stage where that move |
|
| |
|
| 0:12:39.459,0:12:43.880 | | 0:24:04.179,0:24:04.789 |
| the x is rational then the prover just picks
| | is being made. |
| delta equals epsilon, and
| | </toggledisplay> |
|
| |
|
| 0:12:43.880,0:12:48.339
| | ===Strongly telepathic prover=== |
| that's good enough for rational x, right?
| |
| Because for rational x the
| |
|
| |
|
| 0:12:48.339,0:12:51.410
| | ''Spot the error in this'': |
| slope of the line is one so picking delta
| |
| as epsilon is good enough.
| |
|
| |
|
| 0:12:51.410,0:12:55.760
| | {{quotation|Consider the limit problem <math>\displaystyle \lim_{x \to 2} x^2 = 4</math>. The <math>\varepsilon-\delta</math> proof corresponding to this problem would involve a game between a prover and a skeptic. To show that the limit statement is true, it suffices to exhibit a winning strategy for the prover for the game. The strategy is as follows. Pick <math>\delta = \frac{\varepsilon}{|x + 2|}</math>. Let's prove that this works.<br><br>''Specific claim'': For any skeptic-picked <math>\varepsilon > 0</math>, if the prover picks <math>\delta > 0</math> such that <math>\delta = \varepsilon/|x + 2|</math>, then regardless of the <math>x</math> that the skeptic picks with <math>0 < |x - 2| < \delta</math>, we have <math>|x^2 - 4| < \varepsilon</math>.<br><br>''Proof of claim'': We have: <br><math>|x^2 - 4| = |x - 2||x + 2| < \delta|x + 2| = \frac{\varepsilon}{|x + 2|} |x + 2| = \varepsilon</math>}} |
| For irrational x, if the skeptic's planning | |
| to choose an irrational x
| |
|
| |
|
| 0:12:55.760,0:12:59.730
| | The error is as follows: <toggledisplay>Recall the sequence of moves made in the game. First, the skeptic picks <math>\varepsilon > 0 </math>. Then, the prover picks <math>\delta > 0</math>. ''Then'', the skeptic picks a test value of <math>x</math> to challenge the prover's claim of the function being trapped. In particular, this means that at the stage that the prover picks the value of <math>\delta</math>, the prover is ''unaware'' of the value of <math>x</math> that the skeptic plans to pick. Hence, the prover's strategy for choosing <math>\delta</math> cannot use <math>x</math>. Rather, the prover must have a strategy for <math>\delta</math> purely in terms of <math>\varepsilon</math>, which is the only piece of information known to the prover at that stage in the game. |
| then the prover can just choose any delta
| |
| actually. Like just pick
| |
|
| |
|
| 0:12:59.730,0:13:03.880
| | This also explains why we called this error the ''strongly telepathic prover'', i.e., it involved the prover reading the skeptic's mind about future planned moves, which is impermissible. |
| the delta in advance. Like delta is one or | |
| something. Because if x is
| |
|
| |
|
| 0:13:03.880,0:13:10.430
| | Although this strategy is wrong, it can be fixed to get a correct strategy, i.e., this is the right way to ''start'' thinking about how this type of problem could be attacked. What the prover needs to do is pick a choice of <math>\delta</math> that works for all <math>x</math> that the skeptic can pick in the constrained interval. The algebra done here provides some guidelines on how the prover can make such a choice, but another idea, namely, the idea of a ''cut-off value'', is needed to complete the strategy.</toggledisplay> |
| irrational then it's like a constant function
| |
| and therefore, like, for
| |
|
| |
|
| 0:13:10.430,0:13:14.970
| | ===Mildly telepathic prover=== |
| any delta the function is trapped within epsilon
| |
| distance of the given
| |
|
| |
|
| 0:13:14.970,0:13:16.970
| | ''Spot the error in this'': |
| limit. Okay?
| |
|
| |
|
| 0:13:16.970,0:13:19.950 | | {{quotation|Consider the limit problem: <br><math>g(x) = \left \lbrace \begin{array}{ll} x, & x \text{ rational } \\ 0, & x \text{ irrational }\\\end{array}\right.</math><br>We want to show that <math>\displaystyle \lim_{x \to 0} g(x) = 0</math><br>For this game, we need to exhibit a winning strategy for the prover. The winning strategy is as follows. The skeptic first chooses <math>\varepsilon > 0</math>. The prover now makes two cases. If the skeptic is planning to pick a rational value of <math>x</math>, then the prover chooses the strategy <math>\delta = \varepsilon</math>. If the skeptic is planning to choose an irrational value of <math>x</math>, then the prover can pick any <math>\delta</math>.<br>Clearly, the prover's strategy works in both cases, so we have a winning strategy.}} |
| So the prover sort of makes two cases based
| |
| on whether the skeptic
| |
|
| |
|
| 0:13:19.950,0:13:26.950 | | Th error is as follows: <toggledisplay>Recall the sequence of moves made in the game. First, the skeptic picks <math>\varepsilon > 0 </math>. Then, the prover picks <math>\delta > 0</math>. ''Then'', the skeptic picks a test value of <math>x</math> to challenge the prover's claim of the function being trapped. In particular, this means that at the stage that the prover picks the value of <math>\delta</math>, the prover is ''unaware'' of the value of <math>x</math> that the skeptic plans to pick. Hence, the prover's strategy for choosing <math>\delta</math> cannot rely on specifics about what <math>x</math> the skeptic plans to choose. |
| will pick a rational or an irrational x and
| |
| sort of based on that if
| |
|
| |
|
| 0:13:27.040,0:13:30.730
| | This error is similar to the preceding error. Both involve impermissible telepathy on the prover's part in reading the skeptic's mind. The ''strongly telepathic prover'' error is more severe in the sense that it involves the prover reading the exact value of <math>x</math> that the skeptic plans to play, whereas the ''mildly telepathic prover'' error only involves the prover guessing the ''type'' of value (rational or irrational) that the skeptic plans to play. |
| it's rational this is the prover's strategy, | |
| if it's irrational then
| |
|
| |
|
| 0:13:30.730,0:13:34.050
| | The fix for the mildly telepathic prover error is that the prover chooses a ''combined'' strategy that ''simultaneously'' works for both eventualities. In this situation, the strategy <math>\delta = \varepsilon</math> works for both situations (rational and irrational <math>x</math>). In general, for a function with two piece definitions for rational and irrational points in the domain, we need to take the ''min'' of the <math>\delta</math>-strategies that work for the definitions individually. A similar approach works for different definitions on the left and right.</toggledisplay> |
| the prover can just do any delta. | |
|
| |
|
| 0:13:34.050,0:13:37.630
| | ===You say you want a replay?=== |
| Can you tell me what's wrong with this proof?
| |
|
| |
|
| 0:13:37.630,0:13:44.630
| | ''Spot the error in this'': |
| KM: So, you're still kind of basing it on
| |
| what the skeptic is going to
| |
|
| |
|
| 0:13:44.750,0:13:45.800 | | {{quotation|Consider the limit problem <math>\displaystyle \lim_{x \to 1} 2x = 2</math>. Let's think of this in terms of an <math>\varepsilon-\delta</math> game. The skeptic begins by picking <math>\varepsilon = 0.1</math>. The prover chooses <math>\delta = 0.05</math>. The skeptic now chooses <math>x = 0.97</math>. This value of <math>x</math> is within the <math>\delta</math>-distance of <math>1</math>. It's now checked that <math>2x = 1.94</math> is within <math>\varepsilon</math>-distance of the claimed limit <math>2</math>. The prover has thus won the game, and we have established the truth of the limit statement.}} |
| pick next.
| |
|
| |
|
| 0:13:45.800,0:13:49.100
| | The error is as follows: <toggledisplay>This involves ''only one'' play of the <math>\varepsilon-\delta</math> limit game. The prover did win this play of the game. However, for us to declare the limit statement to be true, we need to establish that the prover has a ''winning strategy'' for the game, which means we need to demonstrate how the prover would pick a <math>\delta</math> in terms of each choice of <math>\varepsilon</math> (preferably by specifying <math>\delta</math> explicitly as a function of <math>\varepsilon</math>) and then show that the strategy works for all <math>x</math> within <math>\delta</math>-distance of the point on the domain side. |
| Vipul: Okay. It's actually pretty much the
| |
| same problem [as the
| |
|
| |
|
| 0:13:49.100,0:13:55.449
| | It so happens that in this case, the limit statement is true and the prover did play the game according to one possible winning strategy: <math>\delta = \varepsilon/2</math>. However, since we weren't actually told the winning strategy, let alone given an explanation of why it works, what we're given fails as a proof.</toggledisplay> |
| preceding one], in a somewhat minor form.
| |
| The prover is sort of making
| |
|
| |
|
| 0:13:55.449,0:13:59.959
| | ===Playing to lose=== |
| cases based on what the skeptic is going to
| |
| do next, and choosing a
| |
|
| |
|
| 0:13:59.959,0:14:01.940
| | ''Spot the error in this'': |
| strategy according to that. But the prover
| |
| doesn't actually know what
| |
|
| |
|
| 0:14:01.940,0:14:05.089 | | {{quotation|Here's an easy proof that <math>\lim_{x \to 0} \sin(1/x) = 0</math>. We need to show that the prover has a winning strategy for the game. Let's say the skeptic starts out by picking <math>\varepsilon = 2</math>. The prover then picks <math>\delta = 1/\pi</math>. It can now easily be verified that for <math>0 < |x| < \delta</math>, <math>|\sin(1/x) - 0| < 2</math>, because the <math>\sin</math> function is trapped within <math>[-1,1]</math>. Thus, the prover has succeeded in trapping the function within the $\varepsilon$-interval specified by the skeptic, and hence won the game. The limit statement is therefore true.}} |
| the skeptic is going to do next, so the prover | |
| should actually have a
| |
|
| |
|
| 0:14:05.089,0:14:08.970
| | The error is as follows: <toggledisplay>This involves ''only one'' choice of <math>\varepsilon</math>. The proof does show that with the choice <math>\varepsilon = 2</math>, the prover wins the game. However, in order to show that the limit statement is true, one would need to demonstrate that the prover wins the game for ''every'' possible choice of <math>\varepsilon</math>. In particular, from the skeptic's viewpoint, ''smaller is smarter'', so the prover needs to have a strategy to win the game for arbitrarily small <math>\varepsilon</math>. |
| single strategy that works in both cases.
| |
| If cases will be made to
| |
|
| |
|
| 0:14:08.970,0:14:12.209
| | In fact, the limit statement is false, and for any choice of <math>\varepsilon \le 1</math>, the prover ''cannot'' win the game, because the range of the function on the immediate left and immediate right of zero is <math>[-1,1]</math>.</toggledisplay> |
| prove that the strategy works so the prover
| |
| has to have a single
| |
|
| |
|
| 0:14:12.209,0:14:12.459
| | ==Conceptual definition and various cases== |
| strategy.
| |
|
| |
|
| 0:14:12.449,0:14:15.370
| | ===Formulation of conceptual definition=== |
| Now in this case the strategy we can choose
| | Below is the ''conceptual'' definition of limit. Suppose <math>f</math> is a function defined in a neighborhood of the point <math>c</math>, except possibly at the point <math>c</math> itself. We say that: |
| the prover just, the | |
|
| |
|
| 0:14:15.370,0:14:18.779
| | <math>\lim_{x \to c} f(x) = L</math> |
| prover can pick delta as epsilon because that
| |
| will work in both cases.
| |
|
| |
|
| 0:14:18.779,0:14:20.019
| | if: |
| KM: Exactly.
| |
|
| |
|
| 0:14:20.019,0:14:23.320
| | * For every choice of neighborhood of <math>L</math> (where the term ''neighborhood'' is suitably defined) |
| Vipul: Yeah. But in general if you have two
| | * there exists a choice of neighborhood of <math>c</math> (where the term ''neighborhood'' is suitably defined) such that |
| different piece
| | * for all <math>x \ne c</math> that are in the chosen neighborhood of <math>c</math> |
| | * <math>f(x)</math> is in the chosen neighborhood of <math>L</math>. |
|
| |
|
| 0:14:23.320,0:14:26.579
| | <center>{{#widget:YouTube|id=bE_aKfmUHN8}}</center> |
| definitions then the way you would do it so
| |
| you would pick delta as
| |
|
| |
|
| 0:14:26.579,0:14:30.300 | | Full timed transcript: <toggledisplay> |
| the min [minimum] of the delta that work in
| | 0:00:15.570,0:00:19.570 |
| the two different pieces, | | Vipul: Ok, so in this talk I'm going to |
| | do the conceptual definition |
|
| |
|
| 0:14:30.300,0:14:32.910 | | 0:00:19.570,0:00:26.320 |
| because you sort of want to make sure that
| | of limit, which is important for a number |
| both cases are covered. But
| | of reasons. The main reason |
|
| |
|
| 0:14:32.910,0:14:36.730 | | 0:00:26.320,0:00:31.349 |
| the point is you have to do that -- take
| | is it allows you to construct definitions |
| the min use that rather than
| | of limit, not just for this |
|
| |
|
| 0:14:36.730,0:14:39.730 | | 0:00:31.349,0:00:34.430 |
| just say, "I'm going to choose my delta
| | one variable, function of one variable, two |
| based on what the skeptic is
| | sided limit which you have |
|
| |
|
| 0:14:39.730,0:14:42.589 | | 0:00:34.430,0:00:38.930 |
| going to move next." Okay?
| | hopefully seen before you saw this video. |
| | Also for a number of other |
|
| |
|
| 0:14:42.589,0:14:49.120 | | 0:00:38.930,0:00:43.210 |
| This is a minor form of the same misconception
| | limit cases which will include limits to infinity, |
| that that was there in
| | functions of two |
|
| |
|
| 0:14:49.120,0:14:56.120 | | 0:00:43.210,0:00:47.789 |
| the previous example we saw.
| | variables, etc. So this is a general blueprint |
| | for thinking about |
|
| |
|
| 0:15:04.620,0:15:11.620 | | 0:00:47.789,0:00:54.789 |
| So, this is what I call the mildly telepathic | | limits. So let me put this definition here |
| prover, right? The
| | in front for this. As I am |
|
| |
|
| 0:15:14.970,0:15:18.579 | | 0:00:54.890,0:00:59.289 |
| prover is still behaving telepathically
| | going, I will write things in more general. |
| predicting the skeptic's future
| | So the starting thing is... |
|
| |
|
| 0:15:18.579,0:15:23.740 | | 0:00:59.289,0:01:03.899 |
| moves but it's not so bad. The prover is
| | first of all f should be defined around the |
| just making, like, doing a
| | point c, need not be |
|
| |
|
| 0:15:23.740,0:15:25.470 | | 0:01:03.899,0:01:08.810 |
| coin toss type of telepathy. That isn't
| | defined at c, but should be defined everywhere |
| the only one the prover is
| | around c. I won't write |
|
| |
|
| 0:15:25.470,0:15:30.790 | | 0:01:08.810,0:01:11.750 |
| actually, deciding exactly what x skeptic
| | that down, I don't want to complicate things |
| would take. But it's still
| | too much. So we start |
|
| |
|
| 0:15:30.790,0:15:32.790 | | 0:01:11.750,0:01:18.750 |
| the same problem and the reason why I think
| | with saying for every epsilon greater than |
| people will have this
| | zero. Why are we picking |
|
| |
|
| 0:15:32.790,0:15:36.329 | | 0:01:19.920,0:01:21.689 |
| misconception is because they don't think
| | this epsilon greater than zero? |
| about it in terms of the
| |
|
| |
|
| 0:15:36.329,0:15:38.970 | | 0:01:21.689,0:01:22.790 |
| sequence in which the moves are made, and
| | Rui: Why? |
| the information that each
| |
|
| |
|
| 0:15:38.970,0:15:45.970 | | 0:01:22.790,0:01:26.070 |
| body has at any given stage of the game.
| | Vipul: What is the goal of this epsilon? Where |
| | will it finally appear? |
|
| |
|
| 0:15:50.889,0:15:57.889 | | 0:01:26.070,0:01:28.520 |
| Let's do this one.
| | It will finally appear here. Is this captured? |
|
| |
|
| 0:16:10.930,0:16:15.259 | | 0:01:28.520,0:01:29.520 |
| So, this is a limit game, right? Let's say
| | Rui: Yes. |
| that limit as x approaches
| |
|
| |
|
| 0:16:15.259,0:16:22.259 | | 0:01:29.520,0:01:32.920 |
| 1 of 2x is 2, okay? How do we go about showing
| | Vipul: Which means what we actually are picking |
| this? Well, the idea is
| | when we...if you've |
|
| |
|
| 0:16:23.699,0:16:27.990 | | 0:01:32.920,0:01:37.720 |
| let's play the game, right? Let's say
| | seen the limit as a game video or you know |
| the skeptic it picks epsilon as
| | how to make a limit as a |
|
| |
|
| 0:16:27.990,0:16:34.990 | | 0:01:37.720,0:01:41.700 |
| 0.1, okay? The prover picks delta as 0.05.
| | game. This first thing has been chosen by |
| The skeptic is then picking
| | the skeptic, right, and the |
|
| |
|
| 0:16:35.139,0:16:38.790 | | 0:01:41.700,0:01:45.840 |
| epsilon as 0.1, the skeptic is saying, "Please
| | skeptic is trying to challenge the prover |
| trap the function
| | into trapping f(x) within L - epsilon to |
|
| |
|
| 0:16:38.790,0:16:43.800 | | 0:01:45.840,0:01:50.210 |
| between 1.9 and 2.1. Okay? Find the delta
| | L + epsilon. Even if you haven't |
| small enough so that the
| | seen that [the game], the main focus of |
|
| |
|
| 0:16:43.800,0:16:48.389 | | 0:01:50.210,0:01:55.570 |
| function value is dropped between 1.9 and
| | picking epsilon is to pick this interval surrounding |
| 2.1. The prover picks delta
| | L. So instead of |
|
| |
|
| 0:16:48.389,0:16:55.389 | | 0:01:55.570,0:02:02.570 |
| as 0.05 which means the prover is now getting
| | saying, for every epsilon greater than zero, |
| the input value trap
| | let's say for every |
|
| |
|
| 0:16:57.850,0:17:04.850 | | 0:02:04.259,0:02:11.259 |
| between 0.95 and 1.05. That's 1 plus minus
| | choice of neighborhood of L. So what I mean |
| this thing. And now the
| | by that, I have not |
|
| |
|
| 0:17:05.439,0:17:09.070 | | 0:02:19.650,0:02:23.760 |
| prover is claiming that if the x value is
| | clearly defined it so this is a definition |
| within this much distance of
| | which is not really a |
|
| |
|
| 0:17:09.070,0:17:13.959 | | 0:02:23.760,0:02:28.139 |
| 1 except the value equal to 1, then the function
| | definition, sort of the blueprint for definitions. |
| value is within 0.1
| | It is what you fill |
|
| |
|
| 0:17:13.959,0:17:17.630 | | 0:02:28.139,0:02:31.570 |
| distance of 2. So, the skeptic tries picking
| | in the details [of] and get a correct definition. |
| x within the interval
| | So by neighborhood, |
|
| |
|
| 0:17:17.630,0:17:23.049 | | 0:02:31.570,0:02:36.180 |
| prescribed by the prover, so maybe the skeptic
| | I mean, in this case, I would mean something |
| picks 0.97 which is
| | like (L - epsilon, L + |
|
| |
|
| 0:17:23.049,0:17:26.380 | | 0:02:36.180,0:02:43.180 |
| within 0.05 distance of 1.
| | epsilon). It is an open interval surrounding |
| | L. Ok, this one. The |
|
| |
|
| 0:17:26.380,0:17:31.570 | | 0:02:44.590,0:02:47.160 |
| And then they check that f(x) is 1.94, that
| | conceptual definition starts for every choice |
| is at the distance of 0.06
| | of neighborhood of |
|
| |
|
| 0:17:31.570,0:17:38.570 | | 0:02:47.160,0:02:54.160 |
| from 2. So, it's within 0.1 of the claimed
| | L. The domain neighborhood, I haven't really |
| limit. Who won the game?
| | defined, but that is the |
|
| |
|
| 0:17:38.780,0:17:42.650 | | 0:02:58.359,0:03:05.359 |
| If the thing is within the interval then who
| | point, it is the general conceptual definition. |
| wins?
| | There exists...what |
|
| |
|
| 0:17:42.650,0:17:43.320 | | 0:03:09.810,0:03:11.530 |
| KM: The prover.
| | should come next? [ANSWER!] |
|
| |
|
| 0:17:43.320,0:17:46.720 | | 0:03:11.530,0:03:16.530 |
| Vipul: The prover wins, right? So, the prover | | Rui: A delta? |
| won again so therefore
| | Vipul: That is what the concrete definition |
|
| |
|
| 0:17:46.720,0:17:52.100 | | 0:03:16.530,0:03:18.530 |
| this limit statement is true, right? So, what's
| | says, but what would the |
| wrong with this as a
| | conceptual thing say? |
|
| |
|
| 0:17:52.100,0:17:57.370 | | 0:03:18.530,0:03:21.680 |
| proof that the limit statement is true? How
| | Rui: A neighborhood. |
| is this not a proof that
| | Vipul: Of what? [ANSWER!] |
|
| |
|
| 0:17:57.370,0:18:03.870 | | 0:03:21.680,0:03:28.680 |
| the limit statement is true? This what I've
| | Rui: Of c. |
| written here, why is that
| | Vipul: Of c, of the domain. The goal of picking |
|
| |
|
| 0:18:03.870,0:18:05.990 | | 0:03:34.639,0:03:37.970 |
| not a proof that the limit statement is true?
| | delta is to find a |
| | neighborhood of c. Points to the immediate |
|
| |
|
| 0:18:05.990,0:18:11.960 | | 0:03:37.970,0:03:44.919 |
| KM: Because it's only an example for the
| | left and immediate |
| specific choice of epsilon and x.
| | right of c. There exists a choice of neighborhood |
|
| |
|
| 0:18:11.960,0:18:16.200 | | 0:03:44.919,0:03:51.919 |
| Vipul: Yes, exactly. So, it's like a single
| | of c such that, by |
| play of the game, the
| | the way I sometimes abbreviate, such that, |
|
| |
|
| 0:18:16.200,0:18:20.470 | | 0:03:59.850,0:04:06.109 |
| prover wins, but the limit statement doesn't
| | as s.t., okay, don't get |
| just say that the prover
| | confused by that. Okay, what next? Let's |
|
| |
|
| 0:18:20.470,0:18:24.380 | | 0:04:06.109,0:04:12.309 |
| wins the game, it says the prover has a winning
| | bring out the thing. The next |
| strategy. It says that
| | thing is for all x with |x - c| less than |
|
| |
|
| 0:18:24.380,0:18:27.660 | | 0:04:12.309,0:04:19.309 |
| the prover can win the game regardless of | | ... all x in the neighborhood |
| how the skeptic plays;
| | except the point c itself. So what should |
|
| |
|
| 0:18:27.660,0:18:31.070 | | 0:04:20.040,0:04:27.040 |
| there's a way for the prover to do that.
| | come here? For all x in the |
| This just gives one example
| | neighborhood of c, I put x not equal to c. |
|
| |
|
| 0:18:31.070,0:18:34.640 | | 0:04:36.570,0:04:37.160 |
| where the prover won the game, but it doesn't
| | Is that clear? |
| tell us that regardless
| |
|
| |
|
| 0:18:34.640,0:18:37.280 | | 0:04:37.160,0:04:37.520 |
| of the epsilon the skeptic takes the prover
| | Rui: Yes. |
| can pick a delta such that
| |
|
| |
|
| 0:18:37.280,0:18:41.090 | | 0:04:37.520,0:04:44.520 |
| regardless of the x the skeptic picks, the
| | Vipul: x not equal to c in the neighborhood |
| function is within the
| | chosen for c. The reason |
|
| |
|
| 0:18:41.090,0:18:45.530 | | 0:04:49.310,0:04:53.360 |
| thing. So that's what they should do. Okay?
| | we're excluding the point c that we take the |
| | limit at the point and we |
|
| |
|
| 0:18:45.530,0:18:51.160 | | 0:04:53.360,0:04:55.770 |
| Now you notice -- I'm sure you notice this
| | just care about stuff around, we don't care |
| but the way the game and the
| | about what is happening at |
|
| |
|
| 0:18:51.160,0:18:58.160 | | 0:04:55.770,0:05:02.770 |
| limit definition. The way the limit definition
| | the point. For c...this chosen neighborhood...I |
| goes, you see that all
| | am writing the black |
|
| |
|
| 0:18:59.870,0:19:04.260 | | 0:05:09.880,0:05:14.440 |
| the moves of the skeptic be right "for every" | | for choices that the skeptic makes and the |
| "for all." Right? And
| | red for the choices the |
|
| |
|
| 0:19:04.260,0:19:07.390 | | 0:05:14.440,0:05:16.490 |
| for all the moves of the prover it's "there
| | prover makes, actually that's reverse of what |
| exists." Why do we do
| | I did in the other |
|
| |
|
| 0:19:07.390,0:19:11.140 | | 0:05:16.490,0:05:21.320 |
| that? Because we are trying to get a winning | | video, but that's ok. They can change colors. |
| strategy for the prover,
| | If you have seen that |
|
| |
|
| 0:19:11.140,0:19:14.309 | | 0:05:21.320,0:05:24.710 |
| so the prover controls his own moves. Okay?
| | limit game thing, this color pattern just |
| | [means] ... the black |
|
| |
|
| 0:19:14.309,0:19:15.250 | | 0:05:24.710,0:05:28.400 |
| KM: Exactly.
| | matches with the skeptic choices and the red |
| | matches what the prover |
|
| |
|
| 0:19:15.250,0:19:18.630 | | 0:05:28.400,0:05:32.710 |
| Vipul: So, therefore wherever it's a prover
| | chooses. If you haven't seen that, it is |
| move it will be a there
| | not an issue. Just imagine |
|
| |
|
| 0:19:18.630,0:19:22.240 | | 0:05:32.710,0:05:35.820 |
| exists. Where there is a skeptic's move
| | it's a single color. |
| the prover has to be prepared
| |
|
| |
|
| 0:19:22.240,0:19:29.240 | | 0:05:35.820,0:05:40.820 |
| for anything the skeptic does. All those moves
| | What happens next? What do we need to check |
| are "for every."
| | in order to say this limit |
|
| |
|
| 0:19:30.559,0:19:33.850 | | 0:05:40.820,0:05:42.950 |
| One last one. By the way, this one was called,
| | is L? So f(x) should be where? |
| "You say you want a
| |
|
| |
|
| 0:19:33.850,0:19:36.870 | | 0:05:42.950,0:05:44.980 |
| replay?" Which is basically they're just
| | Rui: In the neighborhood of L. |
| saying that just one play is
| |
|
| |
|
| 0:19:36.870,0:19:40.890 | | 0:05:44.980,0:05:48.060 |
| not good enough. If the statement is actually
| | Vipul: Yeah. In the concrete definition we |
| true, the prover should
| | said f(x) minus L is less |
|
| |
|
| 0:19:40.890,0:19:45.370 | | 0:05:48.060,0:05:51.440 |
| be willing to accept the skeptic ones, the
| | than epsilon. Right, but that is just stating |
| reply and say they want to
| | that f(x) is in the |
|
| |
|
| 0:19:45.370,0:19:47.679 | | 0:05:51.440,0:05:58.440 |
| play it again, the prover should say "sure"
| | chosen neighborhood. So f(x) is in the chosen |
| and "I'm going to win
| | neighborhood of...Now |
|
| |
|
| 0:19:47.679,0:19:53.320 | | 0:06:08.470,0:06:15.470 |
| again." That's what it would mean for
| | that we have this blueprint for the definition. |
| the limit statement to be true. | | This is a blueprint |
|
| |
|
| 0:19:53.320,0:20:00.320 | | 0:06:25.660,0:06:32.660 |
| One last one. Just kind of pretty similar
| | for the definition. We'll write it in blue. |
| to the one we just saw. Just
| | What I mean is, now if I |
|
| |
|
| 0:20:16.690,0:20:23.690 | | 0:06:34.930,0:06:40.700 |
| a little different. | | ask you to define a limit, in a slightly different |
| | context; you just |
|
| |
|
| 0:20:39.020,0:20:46.020 | | 0:06:40.700,0:06:46.280 |
| Okay, this one, let's see. We are saying
| | have to figure out in order to make this rigorous |
| that the limit as x
| | definition. What |
|
| |
|
| 0:20:50.450,0:20:56.900 | | 0:06:46.280,0:06:49.240 |
| approaches zero of sin(1/x) is zero, right?
| | word do you need to understand the meaning |
| Let's see how we prove
| | of? [ANSWER!] |
|
| |
|
| 0:20:56.900,0:21:01.409 | | 0:06:49.240,0:06:53.780 |
| this. If the statement true ... well, do you
| | Rui: Neighborhood. |
| think the statement is
| | Vipul: Neighborhood, right. That's the magic |
|
| |
|
| 0:21:01.409,0:21:08.409 | | 0:06:53.780,0:06:59.810 |
| true? As x approach to zero, is sin 1 over
| | word behind which I am |
| x approaching zero? So
| | hiding the details. If you can understand |
|
| |
|
| 0:21:13.980,0:21:20.980 | | 0:06:59.810,0:07:06.280 |
| here's the picture of sin(1/x). y-axis.
| | what I mean by neighborhood |
| It's an oscillatory function
| | then you can turn this into a concrete definition.</toggledisplay> |
|
| |
|
| 0:21:22.010,0:21:27.870
| | ===Functions of one variable case=== |
| and it has this kind of picture. Does it doesn't
| |
| go to zero as x
| |
|
| |
|
| 0:21:27.870,0:21:29.270
| | The following definitions of neighborhood are good enough to define limits. |
| approaches zero?
| |
|
| |
|
| 0:21:29.270,0:21:30.669
| | * For points in the interior of the domain, for functions of one variable: We can take an open interval centered at the point. For a point <math>c</math>, such an open interval is of the form <math>(c - t, c + t), t > 0</math>. Note that if we exclude the point <math>c</math> itself, we get <math>(c - t,c) \cup (c,c + t)</math>. |
| KM: No.
| | * For the point <math>+\infty</math>, for functions of one variable: We take intervals of the form <math>(a,\infty)</math>, where <math>a \in \R</math>. |
| | * For the point <math>-\infty</math>, for functions of one variable: We can take interval of the form <math>(-\infty,a)</math>, where <math>a \in \R</math>. |
|
| |
|
| 0:21:30.669,0:21:35.539 | | We can now list the nine cases of limits, combining finite and infinite possibilities: |
| Vipul: No. So, you said that this statement
| | |
| is false, but I'm going to
| | {| class="sortable" border="1" |
| | ! Case !! Definition |
| | |- |
| | | <math>\lim_{x \to c} f(x) = L</math> || For every <math>\varepsilon > 0</math>, there exists <math>\delta > 0</math> such that for all <math>x</math> satisfying <math>0 < |x - c| < \delta</math> (i.e., <math>x \in (c - \delta,c) \cup (c,c + \delta)</math>), we have <math>|f(x) - L| < \varepsilon</math> (i.e., <math>f(x) \in (L - \varepsilon,L +\varepsilon)</math>). |
| | |- |
| | | <math>\lim_{x \to c} f(x) = -\infty</math> || For every <math>a \in \R</math>, there exists <math>\delta > 0</math> such that for all <math>x</math> satisfying <math>0 < |x - c| < \delta</math> (i.e., <math>x \in (c - \delta,c) \cup (c,c + \delta)</math>), we have <math>f(x) < a</math> (i.e., <math>f(x) \in (-\infty,a)</math>). |
| | |- |
| | | <math>\lim_{x \to c} f(x) = \infty</math> || For every <math>a \in \R</math>, there exists <math>\delta > 0</math> such that for all <math>x</math> satisfying <math>0 < |x - c| < \delta</math> (i.e., <math>x \in (c - \delta,c) \cup (c,c + \delta)</math>), we have <math>f(x) > a</math> (i.e., <math>f(x) \in (a,\infty)</math>). |
| | |- |
| | | <math>\lim_{x \to -\infty} f(x) = L</math> || For every <math>\varepsilon > 0</math>, there exists <math>a \in \R</math> such that for all <math>x</math> satisfying <math>x < a</math> (i.e., <math>x \in (-\infty,a)</math>), we have <math>|f(x) - L| < \varepsilon</math> (i.e., <math>f(x) \in (L - \varepsilon,L +\varepsilon)</math>). |
| | |- |
| | | <math>\lim_{x \to -\infty} f(x) = -\infty</math> || For every <math>b \in \R</math>, there exists <math>a \in \R</math> such that for all <math>x</math> satisfying <math>x < a</math> (i.e., <math>x \in (-\infty,a)</math>), we have <math>f(x) < b</math> (i.e., <math>f(x) \in (-\infty,b)</math>). |
| | |- |
| | | <math>\lim_{x \to -\infty} f(x) = \infty</math> || For every <math>b \in \R</math>, there exists <math>a \in \R</math> such that for all <math>x</math> satisfying <math>x < a</math> (i.e., <math>x \in (-\infty,a)</math>), we have <math>f(x) > b</math> (i.e., <math>f(x) \in (b,\infty)</math>). |
| | |- |
| | | <math>\lim_{x \to \infty} f(x) = L</math> || For every <math>\varepsilon > 0</math>, there exists <math>a \in \R</math> such that for all <math>x</math> satisfying <math>x > a</math> (i.e., <math>x \in (a,\infty)</math>), we have <math>|f(x) - L| < \varepsilon</math> (i.e., <math>f(x) \in (L - \varepsilon,L +\varepsilon)</math>). |
| | |- |
| | | <math>\lim_{x \to \infty} f(x) = -\infty</math> || For every <math>b \in \R</math>, there exists <math>a \in \R</math> such that for all <math>x</math> satisfying <math>x > a</math> (i.e., <math>x \in (a,\infty)</math>), we have <math>f(x) < b</math> (i.e., <math>f(x) \in (-\infty,b)</math>). |
| | |- |
| | | <math>\lim_{x \to \infty} f(x) = \infty</math> || For every <math>b \in \R</math>, there exists <math>a \in \R</math> such that for all <math>x</math> satisfying <math>x > a</math> (i.e., <math>x \in (a,\infty)</math>), we have <math>f(x) > b</math> (i.e., <math>f(x) \in (b,\infty)</math>). |
| | |} |
|
| |
|
| 0:21:35.539,0:21:38.700
| | <center>{{#widget:YouTube|id=EOQby7b-WrA}}</center> |
| try to show it's true. Here's how I do
| |
| that. Let's say the skeptic
| |
|
| |
|
| 0:21:38.700,0:21:44.510
| | ===Limit of sequence versus real-sense limit=== |
| picks epsilon as two, okay? And then the prover
| |
| ... so, the epsilon is
| |
|
| |
|
| 0:21:44.510,0:21:48.520
| | Recall that the limit of a real-valued function to infinity is defined as follows: |
| two so that's the interval of width two
| |
| about the game limit zero. The
| |
|
| |
|
| 0:21:48.520,0:21:55.150
| | <math>\lim_{x \to \infty} f(x) = L</math> means that: |
| prover picks delta as 1/pi. Whatever x the
| |
| skeptic picks, okay?
| |
|
| |
|
| 0:21:55.150,0:22:02.150 | | * For every <math>\varepsilon > 0</math> |
| Regardless of the x that the
| | * there exists <math>a \in \R</math> (we're thinking of the neighborhood <math>(a,\infty)</math>) such that |
| skeptic picks, the function is trapped
| | * for all <math>x > a</math> (i.e. <math>x \in (a,\infty)</math>) |
| within epsilon of the game limit. Is that
| | * we have <math>|f(x) - L| < \varepsilon</math> (i.e., <math>f(x) \in L - \varepsilon,L + \varepsilon)</math>). |
| | |
| | Suppose now instead that <math>f</math> is a function restricted to the natural numbers. We can think of <math>f</math> as a [[sequence]], namely the sequence <math>f(1), f(2), \dots</math>. In that case: |
|
| |
|
| 0:22:10.340,0:22:16.900
| | <math>\lim_{n \to \infty, n \in \mathbb{N}} f(n) = L</math> (in words, the sequence converges to <math>L</math>) means that: |
| true? Yes, because sin
| |
| (1/x) is between minus 1 and 1, right? Therefore
| |
|
| |
|
| 0:22:16.900,0:22:20.100 | | * For every <math>\varepsilon > 0</math> |
| since the skeptic
| | * there exists <math>n_0 \in \mathbb{N}</math> such that |
| picked an epsilon of 2, the function value
| | * for all <math>n \in \mathbb{N}</math> satisfying <math>n > n_0</math>, |
| | * we have <math>|f(n) - L| < \varepsilon</math> (i.e., <math>f(n) \in (L - \varepsilon, L + \varepsilon)</math>). |
|
| |
|
| 0:22:20.100,0:22:24.030
| | The definitions differ both in their second and third line. However, the difference in the second line (the use of a real number versus a natural number to specify the threshold for the trapping interval) is not important, i.e., we could swap these lines between the definitions without changing the sense of either definition. The key difference between the definitions lies in their third lines. In the real-sense limit definition case, we require trapping of the function value close to the claimed limit for ''all sufficiently large reals'' whereas the sequence limit definition requires trapping only for ''all sufficiently large natural numbers''. |
| is completely trapped in
| |
| the interval from -1 to 1, so therefore the | |
|
| |
|
| 0:22:24.030,0:22:27.919
| | To understand this distinction, consider the following: if <math>f</math> is defined on reals, and it has a real-sense limit, i.e., <math>\lim_{x \to \infty} f(x) = L</math> for some <math>L \in \mathbb{R}</math>, then it must also be true that <math>\lim_{n \to \infty, n \in \mathbb{N}} f(n) = L</math>. However, it is possible for <math>f</math> to have a sequence limit but not have a real-sense limit. For instance, the function <math>f(x) := \sin(\pi x)</math> has <math>\lim_{x \to \infty} f(x)</math> undefined but <math>\lim_{n \to \infty, n \in \mathbb{N}} f(n)</math> is zero, because <math>f</math> takes the value 0 at all integers. |
| prover managed to trap it
| |
| within distance of 2 of the claimed limit zero.
| |
|
| |
|
| 0:22:27.919,0:22:30.970
| | <center>{{#widget:YouTube|id=P9APtpIE4y8}}</center> |
| Okay? Regardless of what
| |
| the skeptic does, right? It's not just saying
| |
|
| |
|
| 0:22:30.970,0:22:34.370
| | Full timed transcript: <toggledisplay> |
| that the prover won the
| |
| game once, it's saying whatever x the skeptic
| |
|
| |
|
| 0:22:34.370,0:22:40.740 | | 0:00:15.530,0:00:22.530 |
| picks the prover can
| | Vipul: Okay. So this talk is going to be about |
| still win the game. Right? Regardless if the
| | limit at infinity for functions on real numbers |
|
| |
|
| 0:22:40.740,0:22:43.780 | | 0:00:24.300,0:00:28.980 |
| x is skeptic picks, the
| | and the concept of limits of sequences, how |
| prover picked a delta such that the function
| | these definitions are essentially almost the |
|
| |
|
| 0:22:43.780,0:22:48.100 | | 0:00:28.980,0:00:34.790 |
| is trapped. It's
| | same thing and how they differ. |
| completely trapped, okay? It's not an issue
| |
|
| |
|
| 0:22:48.100,0:22:51.130 | | 0:00:34.790,0:00:41.790 |
| of whether the skeptic
| | Okay. So let's begin by reviewing the definition |
| picks the stupid x. Do you think that this
| | of the limit as x approaches infinity of f(x). |
|
| |
|
| 0:22:51.130,0:22:52.130 | | 0:00:42.360,0:00:47.390 |
| proves the statement?
| | Or rather what it means for that limit to |
| | be a number L. Well, what it means is that |
|
| |
|
| 0:22:52.130,0:22:59.130 | | 0:00:47.390,0:00:52.699 |
| KM: No, I mean in this case it still depended
| | for every epsilon greater than zero, so we |
| on the epsilon that the
| | first say for every neighborhood of L, small |
|
| |
|
| 0:23:01.030,0:23:01.820 | | 0:00:52.699,0:00:59.429 |
| skeptic chose.
| | neighborhood of L, given by radius epsilon |
| | there exists a neighborhood of infinity which |
|
| |
|
| 0:23:01.820,0:23:04.980 | | 0:00:59.429,0:01:03.010 |
| Vipul: It's still dependent on the epsilon
| | is specified by choosing some a such that |
| that the skeptic chose? So, | | that is |
|
| |
|
| 0:23:04.980,0:23:05.679 | | 0:01:03.010,0:01:08.670 |
| yes, that's exactly the problem.
| | the interval (a,infinity) ... |
|
| |
|
| 0:23:05.679,0:23:09.370 | | 0:01:08.670,0:01:15.220 |
| So, we proved that the statement -- we prove
| | ... such that for all x in the interval from |
| that from this part onward
| | a to infinity. That is for all x within the |
|
| |
|
| 0:23:09.370,0:23:12.500 | | 0:01:15.220,0:01:20.430 |
| but it still, we didn't prove it for all
| | chosen neighborhood of infinity, the f(x) |
| epsilon, we only prove for
| | value is within the chosen neighborhood of |
|
| |
|
| 0:23:12.500,0:23:16.309 | | 0:01:20.430,0:01:23.390 |
| epsilon is 2, and 2 is a very big number,
| | L. Okay? |
| right? Because the
| |
|
| |
|
| 0:23:16.309,0:23:19.970 | | 0:01:23.390,0:01:28.049 |
| oscillation is all happening between minus
| | If you want to think about it in terms of |
| 1 and 1, and if in fact the
| | the game between the prover and the skeptic, |
|
| |
|
| 0:23:19.970,0:23:26.970 | | 0:01:28.049,0:01:34.560 |
| skeptic had pick epsilon as 1 or something
| | the prover is claiming that the limit as x |
| smaller than 1 then the two
| | approaches infinity of f(x) is L. The skeptic |
|
| |
|
| 0:23:27.030,0:23:32.169 | | 0:01:34.560,0:01:38.930 |
| epsilon strip width would not cover the entire | | begins by picking a neighborhood of L which |
| -1, +1
| | is parameterized by its radius epsilon. The |
|
| |
|
| 0:23:32.169,0:23:35.490 | | 0:01:38.930,0:01:41.619 |
| interval, and then whatever the prover did
| | prover picks the |
| the skeptic could actually
| | neighborhood of infinity which is parameterized |
|
| |
|
| 0:23:35.490,0:23:39.530 | | 0:01:41.619,0:01:48.350 |
| pick an x and show that it's not trapped.
| | by its lower end a. Then the skeptic picks |
| So, in fact the reason why
| | a value x between a and infinity. Then they |
|
| |
|
| 0:23:39.530,0:23:43.110 | | 0:01:48.350,0:01:51.990 |
| the prover could win the game from this point
| | check whether absolute value f(x) minus L |
| onward is that the
| | [symbolically: |f(x) - L|] is less than epsilon. |
|
| |
|
| 0:23:43.110,0:23:45.900 | | 0:01:51.990,0:01:56.090 |
| skeptic made of stupid choice of epsilon.
| | That is they check whether f(x) is in the |
| Okay?
| | chosen neighborhood of L (the neighborhood |
|
| |
|
| 0:23:45.900,0:23:52.289 | | 0:01:56.090,0:02:00.640 |
| In all these situation, all these misconceptions,
| | chosen by the skeptic). If it is, |
| the main problem is, | | then the prover wins. The prover has managed |
| | |
| | 0:02:00.640,0:02:05.810 |
| | to trap the function: for x large enough, |
| | the prover has managed to trap the function |
|
| |
|
| 0:23:52.289,0:23:58.919 | | 0:02:05.810,0:02:12.810 |
| that we're not ... keeping in mind the order
| | within epsilon distance of L. If not, then |
| which the moves I made
| | the skeptic wins. The statement is true if |
|
| |
|
| 0:23:58.919,0:24:04.179 | | 0:02:13.610,0:02:18.680 |
| and how much information each claim has at
| | the prover has a winning the strategy for |
| the stage where that move | | the game. |
|
| |
|
| 0:24:04.179,0:24:04.789 | | 0:02:18.680,0:02:21.730 |
| is being made.</toggledisplay> | | Now, there is a similar definition which one |
| | has for sequences. So, what's a sequence? |
|
| |
|
| ===Strongly telepathic prover===
| | 0:02:21.730,0:02:26.349 |
| | Well, it's just a function from the natural |
| | numbers. And, here, we're talking of sequences |
|
| |
|
| ''Spot the error in this'': | | 0:02:26.349,0:02:31.610 |
| | of real numbers. So, it's a function from |
| | the naturals to the reals and we use the same |
|
| |
|
| {{quotation|Consider the limit problem <math>\displaystyle \lim_{x \to 2} x^2 = 4</math>. The <math>\varepsilon-\delta</math> proof corresponding to this problem would involve a game between a prover and a skeptic. To show that the limit statement is true, it suffices to exhibit a winning strategy for the prover for the game. The strategy is as follows. Pick <math>\delta = \frac{\varepsilon}{|x + 2|}</math>. Let's prove that this works.<br><br>''Specific claim'': For any skeptic-picked <math>\varepsilon > 0</math>, if the prover picks <math>\delta > 0</math> such that <math>\delta = \varepsilon/|x + 2|</math>, then regardless of the <math>x</math> that the skeptic picks with <math>0 < |x - 2| < \delta</math>, we have <math>|x^2 - 4| < \varepsilon</math>.<br><br>''Proof of claim'': We have: <br><math>|x^2 - 4| = |x - 2||x + 2| < \delta|x + 2| = \frac{\varepsilon}{|x + 2|} |x + 2| = \varepsilon</math>}}
| | 0:02:31.610,0:02:37.400 |
| | letter f for a good reason. Usually we write |
| | sequences with subscripts, a_n type of thing. |
|
| |
|
| The error is as follows: <toggledisplay>Recall the sequence of moves made in the game. First, the skeptic picks <math>\varepsilon > 0 </math>. Then, the prover picks <math>\delta > 0</math>. ''Then'', the skeptic picks a test value of <math>x</math> to challenge the prover's claim of the function being trapped. In particular, this means that at the stage that the prover picks the vaule of <math>\delta</math>, the prover is ''unaware'' of the value of <math>x</math> that the skeptic plans to pick. Hence, the prover's strategy for choosing <math>\delta</math> cannot use <math>x</math>. Rather, the prover must have a strategy for <math>\delta</math> purely in terms of <math>\varepsilon</math>, which is the only piece of information known to the prover at that stage in the game.
| | 0:02:37.400,0:02:42.409 |
| | But I'm using it as a function just to highlight |
| | the similarities. So, limit as n approaches |
|
| |
|
| This also explains why we called this error the ''strongly telepathic prover'', i.e., it involved the prover reading the skeptic's mind about future planned moves, which is impermissible.
| | 0:02:42.409,0:02:47.519 |
| | infinity, n restricted to the natural numbers |
| | ... Usually if it's clear we're talking of |
|
| |
|
| Although this strategy is wrong, it can be fixed to get a correct strategy, i.e., this is the right way to ''start'' thinking about how this type of problem could be attacked. What the prover needs to do is pick a choice of <math>\delta</math> that works for all <math>x</math> that the skeptic can pick in the constrained interval. The algebra done here provides some guidelines on how the prover can make such a choice, but another idea, namely, the idea of a ''cut-off value'', is needed to complete the strategy.</toggledisplay>
| | 0:02:47.519,0:02:52.830 |
| | a sequence, we can remove this part [pointing |
| | to the n in N constraint specification] just |
|
| |
|
| ===Mildly telepathic prover===
| | 0:02:52.830,0:02:54.980 |
| | say limit n approaches infinity f(n), |
| | but since we want to be really clear here, |
|
| |
|
| ''Spot the error in this'':
| | 0:02:54.980,0:02:57.220 |
| | I have put this line. Okay? |
|
| |
|
| {{quotation|Consider the limit problem: <br><math>g(x) = \left \lbrace \begin{array}{ll} x, & x \text{ rational } \\ 0, & x \text{ irrational }\\\end{array}\right.</math><br>We want to show that <math>\displaystyle \lim_{x \to 0} g(x) = 0$</math><br>For this game, we need to exhibit a winning strategy for the prover. The winning strategy is as follows. The skeptic first chooses <math>\varepsilon > 0$</math>. The prover now makes two cases. If the skeptic is planning to pick a rational value of <math>x</math>, then the prover chooses the strategy <math>\delta = \varepsilon</math>. If the skeptic is planning to choose an irrational value of <math>x</math>, then the prover can pick any <math>\delta</math>.<br>Clearly, the prover's strategy works in both cases, so we have a winning strategy.}}
| | 0:02:57.220,0:03:02.709 |
| | So, this limit equals L means "for every epsilon |
| | greater than 0 ..." So, it starts in the same |
|
| |
|
| Th error is as follows: <toggledisplay>Recall the sequence of moves made in the game. First, the skeptic picks <math>\varepsilon > 0 </math>. Then, the prover picks <math>\delta > 0</math>. ''Then'', the skeptic picks a test value of <math>x</math> to challenge the prover's claim of the function being trapped. In particular, this means that at the stage that the prover picks the vaule of <math>\delta</math>, the prover is ''unaware'' of the value of <math>x</math> that the skeptic plans to pick. Hence, the prover's strategy for choosing <math>\delta</math> cannot rely on specifics about what <math>x</math> the skeptic plans to choose.
| | 0:03:02.709,0:03:09.170 |
| | way. The skeptic picks a neighborhood of L. |
| | Then the next line is a little different but |
|
| |
|
| This error is similar to the preceding error. Both involve impermissible telepathy on the prover's part in reading the skeptic's mind. The ''strongly telepathic prover'' error is more severe in the sense that it involves the prover reading the exact value of <math>x</math> that the skeptic plans to play, whereas the ''mildly telepathic prover'' error only involves the prover guessing the ''type'' of value (rational or irrational) that the skeptic plans to play.
| | 0:03:09.170,0:03:16.170 |
| | that's not really the crucial part. The skeptic |
| | is choosing epsilon. The prover picks n_0, |
|
| |
|
| The fix for the mildly telepathic prover error is that the prover chooses a ''combined'' strategy that ''simultaneously'' works for both eventualities. In this situation, the strategy <math>\delta = \varepsilon</math> works for both situations (rational and irrational <math>x</math>). In general, for a function with two piece definitions for rational and irrational points in the domain, we need to take the ''min'' of the <math>\delta</math>-strategies that work for the definitions individually. A similar approach works for different definitions on the left and right.</toggledisplay>
| | 0:03:18.799,0:03:22.830 |
| | a natural number. Now, here the prover is |
| | picking a real number. Here the prover is |
|
| |
|
| ===You say you want a replay?===
| | 0:03:22.830,0:03:26.700 |
| | picking a natural number. That's not really |
| | the big issue. You could in fact change this |
|
| |
|
| ''Spot the error in this'': | | 0:03:26.700,0:03:33.659 |
| | line to match. You could interchange these |
| | lines. It wouldn't affect either definition. |
|
| |
|
| {{quotation|Consider the limit problem <math>\displaystyle \lim_{x \to 1} 2x = 2</math>. Let's think of this in terms of an <math>\varepsilon-\delta</math> game. The skeptic begins by picking <math>\varepsilon = 0.1</math>. The prover chooses <math>\delta = 0.05</math>. The skeptic now chooses <math>x = 0.97</math>. This value of <math>x</math> is within the <math>\delta</math>-distance of <math>1</math>. It's now checked that <math>2x = 1.94</math> is within <math>\varepsilon</math>-distance of the claimed limit <math>2</math>. The prover has thus won the game, and we have established the truth of the limit statement.}}
| | 0:03:33.659,0:03:40.599 |
| | The next line is the really important one |
| | which is different. In here [pointing to real-sense |
|
| |
|
| The error is as follows: <toggledisplay>This involves ''only one'' play of the <math>\varepsilon-\delta</math> limit game. The prover did win this play of the game. However, for us to declare the limit statement to be true, we need to establish that the prover has a ''winning strategy'' for the game, which means we need to demonstrate how the prover would pick a <math>\delta</math> in terms of each choice of <math>\varepsilon</math> (preferably by specifying <math>\delta</math> explicitly as a function of <math>\varepsilon</math>) and then show that the strategy works for all <math>x</math> within <math>\delta</math>-distance of the point on the domain side.
| | 0:03:40.599,0:03:47.430 |
| | limit], the condition has to be valid for |
| | all x, for all real numbers x which are bigger |
|
| |
|
| It so happens that in this case, the limit statement is true and the prover did play the game according to one possible winning strategy: <math>\delta = \varepsilon/2</math>. However, since we weren't actually told the winning strategy, let alone given an explanation of why it works, what we're given fails as a proof.</toggledisplay>
| | 0:03:47.430,0:03:51.900 |
| | than the threshold which the prover has chosen. |
| | Here on the other hand [pointing to the sequence |
|
| |
|
| ===Playing to lose===
| | 0:03:51.900,0:03:56.970 |
| | limit] the condition has to be valid for all |
| | natural numbers which are bigger than the |
|
| |
|
| ''Spot the error in this'':
| | 0:03:56.970,0:04:00.659 |
| | threshold the prover has chosen. By the way, |
| | some of you may have seen the definition with |
|
| |
|
| {{quotation|Here's an easy proof that <math>\lim_{x \to 0} \sin(1/x) = 0</math>. We need to show that the prover has a winning strategy for the game. Let's say the skeptic starts out by picking <math>\varepsilon = 2</math>. The prover then picks <math>\delta = 1/\pi</math>. It can now easily be verified that for <math>0 < |x| < \delta</math>, <math>|\sin(1/x) - 0| < 2</math>, because the <math>\sin</math> function is trapped within <math>[-1,1]</math>. Thus, the prover has succeeded in trapping the function within the $\varepsilon$-interval specified by the skeptic, and hence won the game. The limit statement is therefore true.}}
| | 0:04:00.659,0:04:07.659 |
| | an equality sign here. It doesn't make a difference |
| | to the definition. It does affect what n_0 |
|
| |
|
| The error is as follows: <toggledisplay>This involves ''only one'' choice of <math>\varepsilon</math>. The proof does show that with the choice <math>\varepsilon = 2</math>, the prover wins the game. However, in order to show that the limit statement is true, one would need to demonstrate that the prover wins the game for ''every'' possible choice of <math>\varepsilon</math>. In particular, from the skeptic's viewpoint, ''smaller is smarter'', so the prover needs to have a strategy to win the game for arbitrarily small <math>\varepsilon</math>.
| | 0:04:09.010,0:04:12.019 |
| | you can choose, it will go up or down by one, |
| | but that's not |
|
| |
|
| In fact, the limit statement is false, and for any choice of <math>\varepsilon \le 1</math>, the prover ''cannot'' win the game, because the range of the function on the immediate left and immediate right of zero is <math>[-1,1]</math>.</toggledisplay>
| | 0:04:12.019,0:04:17.310 |
| | really a big issue. The big issue, the big |
| | difference between these two definitions is |
|
| |
|
| ==Conceptual definition and various cases==
| | 0:04:17.310,0:04:23.050 |
| | that in this definition you are insisting |
| | that the condition here is valid for all real |
|
| |
|
| ===Formulation of conceptual definition===
| | 0:04:23.050,0:04:30.050 |
| Below is the ''conceptual'' definition of limit. Suppose <math>f</math> is a function defined in a neighborhood of the point <math>c</math>, except possibly at the point <math>c</math> itself. We say that:
| | x. So, you are insisting or rather the game |
| | is forcing the prover to figure out how to |
|
| |
|
| <math>\lim_{x \to c} f(x) = L</math>
| | 0:04:31.650,0:04:36.940 |
| | trap the function values for all real x. Whereas |
| | here, the game is only requiring the prover |
|
| |
|
| if:
| | 0:04:36.940,0:04:39.639 |
| | to trap the function values for all large |
| | enough |
|
| |
|
| * For every choice of neighborhood of <math>L</math> (where the term ''neighborhood'' is suitably defined)
| | 0:04:39.639,0:04:42.880 |
| * there exists a choice of neighborhood of <math>c</math> (where the term ''neighborhood'' is suitably defined) such that
| | natural numbers. So, here [real-sense limit] |
| * for all <math>x \ne c</math> that are in the chosen neighborhood of <math>c</math>
| | it's all large enough real numbers. Here [sequence |
| * <math>f(x)</math> is in the chosen neighborhood of <math>L</math>.
| |
|
| |
|
| <center>{{#widget:YouTube|id=bE_aKfmUHN8}}</center>
| | 0:04:42.880,0:04:49.250 |
| | limit] it's all large enough natural numbers. |
| | Okay? |
|
| |
|
| Full timed transcript: <toggledisplay>
| | 0:04:49.250,0:04:56.250 |
| 0:00:15.570,0:00:19.570 | | So, that's the only difference essentially. |
| Vipul: Ok, so in this talk I'm going to
| | Now, you can see from the way we have written |
| do the conceptual definition
| |
|
| |
|
| 0:00:19.570,0:00:26.320 | | 0:04:57.050,0:04:59.900 |
| of limit, which is important for a number
| | this that this [real-sense limit] is much |
| of reasons. The main reason
| | stronger. So, if you do have a function which |
|
| |
|
| 0:00:26.320,0:00:31.349 | | 0:04:59.900,0:05:06.880 |
| is it allows you to construct definitions | | is defined on real so that both of these concepts |
| of limit, not just for this
| | can be discussed. If it were just a sequence |
|
| |
|
| 0:00:31.349,0:00:34.430 | | 0:05:06.880,0:05:10.080 |
| one variable, function of one variable, two
| | and there were no function to talk about then |
| sided limit which you have
| | obviously, we can't even talk about this. |
|
| |
|
| 0:00:34.430,0:00:38.930 | | 0:05:10.080,0:05:16.860 |
| hopefully seen before you saw this video.
| | If there's a function defined on the reals |
| Also for a number of other
| | or on all large enough reals, then we can |
|
| |
|
| 0:00:38.930,0:00:43.210 | | 0:05:16.860,0:05:21.470 |
| limit cases which will include limits to infinity, | | try taking both of these. The existence of |
| functions of two
| | this [pointing at the real-sense limit] and |
|
| |
|
| 0:00:43.210,0:00:47.789 | | 0:05:21.470,0:05:24.580 |
| variables, etc. So this is a general blueprint
| | [said "or", meant "and"] it's being equal |
| for thinking about
| | to L as much stronger than this [the sequence |
|
| |
|
| 0:00:47.789,0:00:54.789 | | 0:05:24.580,0:05:27.250 |
| limits. So let me put this definition here
| | limit] equal to L. If this is equal to L then |
| in front for this. As I am
| | definitely this [the sequence limit] is equal |
|
| |
|
| 0:00:54.890,0:00:59.289 | | 0:05:27.250,0:05:29.330 |
| going, I will write things in more general.
| | to L. Okay? |
| So the starting thing is...
| |
|
| |
|
| 0:00:59.289,0:01:03.899 | | 0:05:29.330,0:05:32.080 |
| first of all f should be defined around the
| | But maybe there are situations where this |
| point c, need not be
| | [the sequence limit] is equal to some number |
|
| |
|
| 0:01:03.899,0:01:08.810 | | 0:05:32.080,0:05:38.240 |
| defined at c, but should be defined everywhere
| | but this thing [the real-sense limit] doesn't |
| around c. I won't write
| | exist. So, I want to take one example here. |
|
| |
|
| 0:01:08.810,0:01:11.750 | | 0:05:38.240,0:05:45.240 |
| that down, I don't want to complicate things
| | I have written down an example and we can |
| too much. So we start
| | talk a bit about that is this. So, here is |
|
| |
|
| 0:01:11.750,0:01:18.750 | | 0:05:45.509,0:05:52.509 |
| with saying for every epsilon greater than
| | a function. f(x) = sin(pi x). This is sin |
| zero. Why are we picking
| | (pi x) and the corresponding |
|
| |
|
| 0:01:19.920,0:01:21.689 | | 0:05:55.630,0:06:00.530 |
| this epsilon greater than zero?
| | function if you just restrict [it] to the |
| | natural numbers is just sin (pi n). Now, what |
|
| |
|
| 0:01:21.689,0:01:22.790 | | 0:06:00.530,0:06:06.759 |
| Rui: Why?
| | does sin (pi n) look like for a natural number |
| | n? In fact for any integer n? pi times |
|
| |
|
| 0:01:22.790,0:01:26.070 | | 0:06:06.759,0:06:13.759 |
| Vipul: What is the goal of this epsilon? Where
| | n is an integer multiple of pi. sin of integer |
| will it finally appear?
| | multiples of pi is zero. Let's make a picture |
|
| |
|
| 0:01:26.070,0:01:28.520 | | 0:06:18.370,0:06:25.370 |
| It will finally appear here. Is this captured?
| | of sin ... |
|
| |
|
| 0:01:28.520,0:01:29.520 | | 0:06:27.289,0:06:33.360 |
| Rui: Yes.
| | It's oscillating. Right? Integer multiples |
| | of pi are precisely the ones where it's meeting |
|
| |
|
| 0:01:29.520,0:01:32.920 | | 0:06:33.360,0:06:40.330 |
| Vipul: Which means what we actually are picking
| | the axis. So, in fact we are concerned about |
| when we...if you've
| | the positive one because we are talking of |
|
| |
|
| 0:01:32.920,0:01:37.720 | | 0:06:40.330,0:06:45.840 |
| seen the limit as a game video or you know
| | the sequence (natural number [inputs]). Okay? |
| how to make a limit as a
| | And so, if you are looking at this sequence, |
|
| |
|
| 0:01:37.720,0:01:41.700 | | 0:06:45.840,0:06:51.090 |
| game. This first thing has been chosen by
| | all the terms here are zero. So, the limit |
| the skeptic, right, and the
| | is also zero. So, this limit [the sequence |
|
| |
|
| 0:01:41.700,0:01:45.840 | | 0:06:51.090,0:06:53.030 |
| skeptic is trying to challenge the prover
| | limit] is zero. |
| into trapping f(x) within L - epsilon to
| |
|
| |
|
| 0:01:45.840,0:01:50.210 | | 0:06:53.030,0:07:00.030 |
| L + epsilon. Even if you haven't
| | Okay. What about this limit? Well, we have |
| seen that [the game], the main focus of
| | the picture again. Is it going anywhere? No. |
|
| |
|
| 0:01:50.210,0:01:55.570 | | 0:07:05.349,0:07:07.650 |
| picking epsilon is to pick this interval surrounding
| | It's oscillating between minus one and one |
| L. So instead of
| | [symbolically: oscillating in [-1,1]]. It's |
|
| |
|
| 0:01:55.570,0:02:02.570 | | 0:07:07.650,0:07:11.669 |
| saying, for every epsilon greater than zero,
| | not settling down to any number. It's not... |
| let's say for every
| | You cannot trap it near any particular number |
|
| |
|
| 0:02:04.259,0:02:11.259 | | 0:07:11.669,0:07:17.280 |
| choice of neighborhood of L. So what I mean
| | because it's all over the map between minus |
| by that, I have not
| | one and one. For the same reason that sin(1/x) |
|
| |
|
| 0:02:19.650,0:02:23.760 | | 0:07:17.280,0:07:22.840 |
| clearly defined it so this is a definition
| | doesn't approach anything as x approaches |
| which is not really a
| | zero, the same reason sin x or sin(pi x) doesn't |
| | |
| 0:02:23.760,0:02:28.139
| |
| definition, sort of the blueprint for definitions.
| |
| It is what you fill
| |
|
| |
|
| 0:02:28.139,0:02:31.570 | | 0:07:22.840,0:07:29.840 |
| in the details [of] and get a correct definition.
| | approach anything as x approaches infinity. |
| So by neighborhood, | | So, the limit for the real thing, this does |
|
| |
|
| 0:02:31.570,0:02:36.180 | | 0:07:31.099,0:07:37.539 |
| I mean, in this case, I would mean something
| | not exist. So, this gives an example where |
| like (L - epsilon, L +
| | the real thing [the real-sense limit] doesn't |
| | | |
| 0:02:36.180,0:02:43.180
| | 0:07:37.539,0:07:44.539 |
| epsilon). It is an open interval surrounding
| | exist and the sequence thing [sequence limit] |
| L. Ok, this one. The
| | does exist and so here is the overall summary. |
| | |
| 0:02:44.590,0:02:47.160
| |
| conceptual definition starts for every choice
| |
| of neighborhood of
| |
| | |
| 0:02:47.160,0:02:54.160
| |
| L. The domain neighborhood, I haven't really
| |
| defined, but that is the
| |
| | |
| 0:02:58.359,0:03:05.359
| |
| point, it is the general conceptual definition.
| |
| There exists...what
| |
| | |
| 0:03:09.810,0:03:11.530
| |
| should come next? [ANSWER!]
| |
| | |
| 0:03:11.530,0:03:16.530
| |
| Rui: A delta?
| |
| Vipul: That is what the concrete definition
| |
| | |
| 0:03:16.530,0:03:18.530
| |
| says, but what would the
| |
| conceptual thing say?
| |
| | |
| 0:03:18.530,0:03:21.680
| |
| Rui: A neighborhood.
| |
| Vipul: Of what? [ANSWER!]
| |
| | |
| 0:03:21.680,0:03:28.680
| |
| Rui: Of c.
| |
| Vipul: Of c, of the domain. The goal of picking
| |
| | |
| 0:03:34.639,0:03:37.970
| |
| delta is to find a
| |
| neighborhood of c. Points to the immediate
| |
| | |
| 0:03:37.970,0:03:44.919
| |
| left and immediate
| |
| right of c. There exists a choice of neighborhood
| |
| | |
| 0:03:44.919,0:03:51.919
| |
| of c such that, by
| |
| the way I sometimes abbreviate, such that,
| |
| | |
| 0:03:59.850,0:04:06.109
| |
| as s.t., okay, don't get
| |
| confused by that. Okay, what next? Let's
| |
| | |
| 0:04:06.109,0:04:12.309
| |
| bring out the thing. The next
| |
| thing is for all x with |x - c| less than
| |
| | |
| 0:04:12.309,0:04:19.309 | |
| ... all x in the neighborhood
| |
| except the point c itself. So what should
| |
| | |
| 0:04:20.040,0:04:27.040
| |
| come here? For all x in the
| |
| neighborhood of c, I put x not equal to c.
| |
| | |
| 0:04:36.570,0:04:37.160
| |
| Is that clear?
| |
| | |
| 0:04:37.160,0:04:37.520
| |
| Rui: Yes.
| |
| | |
| 0:04:37.520,0:04:44.520
| |
| Vipul: x not equal to c in the neighborhood
| |
| chosen for c. The reason
| |
| | |
| 0:04:49.310,0:04:53.360
| |
| we're excluding the point c that we take the
| |
| limit at the point and we
| |
| | |
| 0:04:53.360,0:04:55.770
| |
| just care about stuff around, we don't care
| |
| about what is happening at
| |
| | |
| 0:04:55.770,0:05:02.770
| |
| the point. For c...this chosen neighborhood...I
| |
| am writing the black
| |
| | |
| 0:05:09.880,0:05:14.440
| |
| for choices that the skeptic makes and the
| |
| red for the choices the
| |
| | |
| 0:05:14.440,0:05:16.490
| |
| prover makes, actually that's reverse of what
| |
| I did in the other
| |
| | |
| 0:05:16.490,0:05:21.320
| |
| video, but that's ok. They can change colors.
| |
| If you have seen that
| |
| | |
| 0:05:21.320,0:05:24.710
| |
| limit game thing, this color pattern just
| |
| [means] ... the black | |
| | |
| 0:05:24.710,0:05:28.400
| |
| matches with the skeptic choices and the red
| |
| matches what the prover
| |
| | |
| 0:05:28.400,0:05:32.710
| |
| chooses. If you haven't seen that, it is
| |
| not an issue. Just imagine
| |
| | |
| 0:05:32.710,0:05:35.820
| |
| it's a single color.
| |
| | |
| 0:05:35.820,0:05:40.820
| |
| What happens next? What do we need to check
| |
| in order to say this limit
| |
|
| |
|
| 0:05:40.820,0:05:42.950 | | 0:07:44.690,0:07:46.979 |
| is L? So f(x) should be where? | | If the real sense limit, |
| | that is this one [pointing to definition of |
|
| |
|
| 0:05:42.950,0:05:44.980 | | 0:07:46.979,0:07:51.039 |
| Rui: In the neighborhood of L.
| | real sense limit] exists, [then] the sequence |
| | limit also exists and they're both equal. |
|
| |
|
| 0:05:44.980,0:05:48.060 | | 0:07:51.039,0:07:54.419 |
| Vipul: Yeah. In the concrete definition we
| | On the other hand, you can have a situation |
| said f(x) minus L is less
| | with the real sense limit, the limit for the |
|
| |
|
| 0:05:48.060,0:05:51.440 | | 0:07:54.419,0:08:00.819 |
| than epsilon. Right, but that is just stating
| | function of reals doesn't exist but the sequence |
| that f(x) is in the
| | limit still exists like this set up. Right? |
|
| |
|
| 0:05:51.440,0:05:58.440 | | 0:08:00.819,0:08:05.569 |
| chosen neighborhood. So f(x) is in the chosen
| | Now, there is a little caveat that I want |
| neighborhood of...Now
| | to add. If the real sense limit doesn't exist |
|
| |
|
| 0:06:08.470,0:06:15.470 | | 0:08:05.569,0:08:11.069 |
| that we have this blueprint for the definition.
| | as a finite number but it's say plus infinity |
| This is a blueprint
| | then the sequence limit also has to be plus |
|
| |
|
| 0:06:25.660,0:06:32.660 | | 0:08:11.069,0:08:16.150 |
| for the definition. We'll write it in blue.
| | infinity. If the real sense limit is minus |
| What I mean is, now if I
| | infinity, then the sequence limit also has |
|
| |
|
| 0:06:34.930,0:06:40.700 | | 0:08:16.150,0:08:20.330 |
| ask you to define a limit, in a slightly different
| | to be minus infinity. So, this type of situation, |
| context; you just
| | where the real sense limit doesn't exist but |
|
| |
|
| 0:06:40.700,0:06:46.280 | | 0:08:20.330,0:08:26.840 |
| have to figure out in order to make this rigorous
| | the sequence exists, well, will happen in |
| definition. What
| | kind of oscillatory type of situations. Where |
|
| |
|
| 0:06:46.280,0:06:49.240 | | 0:08:26.840,0:08:31.409 |
| word do you need to understand the meaning
| | the real sense you have an oscillating thing |
| of? [ANSWER!]
| | and in the sequence thing on the other hand |
|
| |
|
| 0:06:49.240,0:06:53.780 | | 0:08:31.409,0:08:36.330 |
| Rui: Neighborhood.
| | you somehow manage to pick a bunch of points |
| Vipul: Neighborhood, right. That's the magic
| | where that oscillation doesn't create a problem. |
|
| |
|
| 0:06:53.780,0:06:59.810 | | 0:08:36.330,0:08:36.789 |
| word behind which I am
| | Okay? |
| hiding the details. If you can understand
| |
|
| |
|
| 0:06:59.810,0:07:06.280 | | 0:08:36.789,0:08:43.630 |
| what I mean by neighborhood
| | Now, why is this important? Well, it's important |
| then you can turn this into a concrete definition.</toggledisplay>
| | because in a lot of cases when you have to |
|
| |
|
| ===Functions of one variable case===
| | 0:08:43.630,0:08:50.630 |
| | calculate limits of sequences, you just calculate |
| | them by doing, essentially, just calculating |
|
| |
|
| The following definitions of neighborhood are good enough to define limits.
| | 0:08:53.230,0:09:00.230 |
| | the limits of the function defining the sequence |
| | as a limit of a real valued function. Okay? |
|
| |
|
| * For points in the interior of the domain, for functions of one variable: We can take an open interval centered at the point. For a point <math>c</math>, such an open interval is of the form <math>(c - t, c + t), t > 0</math>. Note that if we exclude the point <math>c</math> itself, we get <math>(c - t,c) \cup (c,c + t)</math>.
| | 0:09:00.230,0:09:03.460 |
| * For the point <math>+\infty</math>, for functions of one variable: We take intervals of the form <math>(a,\infty)</math>, where <math>a \in \R</math>.
| | So, for instance if I ask you what is limit |
| * For the point <math>-\infty</math>, for functions of one variable: We can take interval of the form <math>(-\infty,a)</math>, where <math>a \in \R</math>.
| | ... |
|
| |
|
| We can now list the nine cases of limits, combining finite and infinite possibilities:
| | 0:09:03.460,0:09:10.460 |
| | Okay. I'll ask you what is limit [as] n approaches |
| | infinity of n^2(n + 1)/(n^3 + 1) or something |
|
| |
|
| {| class="sortable" border="1"
| | 0:09:15.200,0:09:22.200 |
| ! Case !! Definition
| | like that. Right? Some rational function. |
| |-
| | You just do this calculation as if you were |
| | <math>\lim_{x \to c} f(x) = L</math> || For every <math>\varepsilon > 0</math>, there exists <math>\delta > 0</math> such that for all <math>x</math> satisfying <math>0 < |x - c| < \delta</math> (i.e., <math>x \in (c - \delta,c) \cup (c,c + \delta)</math>), we have <math>|f(x) - L| < \varepsilon</math> (i.e., <math>f(x) \in (L - \varepsilon,L +\varepsilon)</math>).
| |
| |-
| |
| | <math>\lim_{x \to c} f(x) = -\infty</math> || For every <math>a \in \R</math>, there exists <math>\delta > 0</math> such that for all <math>x</math> satisfying <math>0 < |x - c| < \delta</math> (i.e., <math>x \in (c - \delta,c) \cup (c,c + \delta)</math>), we have <math>f(x) < a</math> (i.e., <math>f(x) \in (-\infty,a)</math>).
| |
| |-
| |
| | <math>\lim_{x \to c} f(x) = \infty</math> || For every <math>a \in \R</math>, there exists <math>\delta > 0</math> such that for all <math>x</math> satisfying <math>0 < |x - c| < \delta</math> (i.e., <math>x \in (c - \delta,c) \cup (c,c + \delta)</math>), we have <math>f(x) > a</math> (i.e., <math>f(x) \in (a,\infty)</math>).
| |
| |-
| |
| | <math>\lim_{x \to -\infty} f(x) = L</math> || For every <math>\varepsilon > 0</math>, there exists <math>a \in \R</math> such that for all <math>x</math> satisfying <math>x < a</math> (i.e., <math>x \in (-\infty,a)</math>), we have <math>|f(x) - L| < \varepsilon</math> (i.e., <math>f(x) \in (L - \varepsilon,L +\varepsilon)</math>).
| |
| |-
| |
| | <math>\lim_{x \to -\infty} f(x) = -\infty</math> || For every <math>b \in \R</math>, there exists <math>a \in \R</math> such that for all <math>x</math> satisfying <math>x < a</math> (i.e., <math>x \in (-\infty,a)</math>), we have <math>f(x) < b</math> (i.e., <math>f(x) \in (-\infty,b)</math>).
| |
| |-
| |
| | <math>\lim_{x \to -\infty} f(x) = \infty</math> || For every <math>b \in \R</math>, there exists <math>a \in \R</math> such that for all <math>x</math> satisfying <math>x < a</math> (i.e., <math>x \in (-\infty,a)</math>), we have <math>f(x) > b</math> (i.e., <math>f(x) \in (b,\infty)</math>).
| |
| |-
| |
| | <math>\lim_{x \to \infty} f(x) = L</math> || For every <math>\varepsilon > 0</math>, there exists <math>a \in \R</math> such that for all <math>x</math> satisfying <math>x > a</math> (i.e., <math>x \in (a,\infty)</math>), we have <math>|f(x) - L| < \varepsilon</math> (i.e., <math>f(x) \in (L - \varepsilon,L +\varepsilon)</math>).
| |
| |-
| |
| | <math>\lim_{x \to \infty} f(x) = -\infty</math> || For every <math>b \in \R</math>, there exists <math>a \in \R</math> such that for all <math>x</math> satisfying <math>x > a</math> (i.e., <math>x \in (a,\infty)</math>), we have <math>f(x) < b</math> (i.e., <math>f(x) \in (-\infty,b)</math>).
| |
| |-
| |
| | <math>\lim_{x \to \infty} f(x) = \infty</math> || For every <math>b \in \R</math>, there exists <math>a \in \R</math> such that for all <math>x</math> satisfying <math>x > a</math> (i.e., <math>x \in (a,\infty)</math>), we have <math>f(x) > b</math> (i.e., <math>f(x) \in (b,\infty)</math>).
| |
| |}
| |
|
| |
|
| <center>{{#widget:YouTube|id=EOQby7b-WrA}}</center>
| | 0:09:25.430,0:09:29.720 |
| | just doing a limit of a real function, function |
| | of real numbers, right? The answer you get |
|
| |
|
| ===Limit of sequence versus real-sense limit===
| | 0:09:29.720,0:09:33.060 |
| | will be the correct one. If it's a finite |
| | number it will be the same finite number. |
|
| |
|
| Recall that the limit of a real-valued function to infinity is defined as follows:
| | 0:09:33.060,0:09:37.850 |
| | In this case it will just be one. But any |
| | rational function, if the answer is finite, |
|
| |
|
| <math>\lim_{x \to \infty} f(x) = L</math> means that:
| | 0:09:37.850,0:09:44.070 |
| | same answer for the sequence. If it is plus |
| | infinity, same answer for the sequence. If |
|
| |
|
| * For every <math>\varepsilon > 0</math>
| | 0:09:44.070,0:09:46.250 |
| * there exists <math>a \in \R</math> (we're thinking of the neighborhood <math>(a,\infty)</math>) such that
| | it is minus infinity, same answer as for the |
| * for all <math>x > a</math> (i.e. <math>x \in (a,\infty)</math>)
| | sequence. |
| * we have <math>|f(x) - L| < \varepsilon</math> (i.e., <math>f(x) \in L - \varepsilon,L + \varepsilon)</math>).
| |
|
| |
|
| Suppose now instead that <math>f</math> is a function restricted to the natural numbers. We can think of <math>f</math> as a [[sequence]], namely the sequence <math>f(1), f(2), \dots</math>. In that case:
| | 0:09:46.250,0:09:53.250 |
| | However, if the answer you get for the real-sense |
| | limit is oscillatory type of non existence, |
|
| |
|
| <math>\lim_{n \to \infty, n \in \mathbb{N}} f(n) = L</math> (in words, the sequence converges to <math>L</math>) means that:
| | 0:09:54.660,0:09:59.410 |
| | | then that's inconclusive as far as the sequence |
| * For every <math>\varepsilon > 0</math>
| | is concerned. You actually have to think about |
| * there exists <math>n_0 \in \mathbb{N}</math> such that
| |
| * for all <math>n \in \mathbb{N}</math> satisfying <math>n > n_0</math>,
| |
| * we have <math>|f(n) - L| < \varepsilon</math> (i.e., <math>f(n) \in (L - \varepsilon, L + \varepsilon)</math>).
| |
|
| |
|
| The definitions differ both in their second and third line. However, the difference in the second line (the use of a real number versus a natural number to specify the threshold for the trapping interval) is not important, i.e., we could swap these lines between the definitions without changing the sense of either definition. The key difference between the definitions lies in their third lines. In the real-sense limit definition case, we require trapping of the function value close to the claimed limit for ''all sufficiently large reals'' whereas the sequence limit definition requires trapping only for ''all sufficiently large natural numbers''.
| | 0:09:59.410,0:10:05.520 |
| | the sequence case and figure out for yourself |
| | what happens to the limit. Okay? If might |
|
| |
|
| To understand this distinction, consider the following: if <math>f</math> is defined on reals, and it has a real-sense limit, i.e., <math>\lim_{x \to \infty} f(x) = L</math> for some <math>L \in \mathbb{R}</math>, then it must also be true that <math>\lim_{n \to \infty, n \in \mathbb{N}} f(n) = L</math>. However, it is possible for <math>f</math> to have a sequence limit but not have a real-sense limit. For instance, the function <math>f(x) := \sin(\pi x)</math> has <math>\lim_{x \to \infty} f(x)</math> undefined but <math>\lim_{n \to \infty, n \in \mathbb{N}} f(n)</math> is zero, because <math>f</math> takes the value 0 at all integers.
| | 0:10:05.520,0:10:07.230 |
| | in |
| | fact be the case that the sequence limit actually |
|
| |
|
| <center>{{#widget:YouTube|id=P9APtpIE4y8}}</center>
| | 0:10:07.230,0:10:11.380 |
| | does exist even though the real sense [limit] |
| | is oscillatory. Okay. |
| | </toggledisplay> |
|
| |
|
| ===Real-valued functions of multiple variables case=== | | ===Real-valued functions of multiple variables case=== |
| Line 5,159: |
Line 5,150: |
| * we have <math>|f(\overline{x}) - L| < \varepsilon</math>. Note that <math>f(\overline{x})</math> and <math>L</math> are both scalars, so the <math>| \cdot |</math> here is the usual [[absolute value function]]. | | * we have <math>|f(\overline{x}) - L| < \varepsilon</math>. Note that <math>f(\overline{x})</math> and <math>L</math> are both scalars, so the <math>| \cdot |</math> here is the usual [[absolute value function]]. |
|
| |
|
| <center>{{#widget:YouTube|id=HZcYxcZplFA}}</center> | | <center>{{#widget:YouTube|id=usb3jew_QVI}}</center> |
ORIGINAL FULL PAGE: Limit
STUDY THE TOPIC AT MULTIPLE LEVELS:
ALSO CHECK OUT: Quiz (multiple choice questions to test your understanding) |Page with videos on the topic, both embedded and linked to
This page lists a core term of calculus. The term is used widely, and a thorough understanding of its definition is critical.
See a complete list of core terminology
Motivation
Quick summary
The term "limit" in mathematics is closely related to one of the many senses in which the term "limit" is used in day-to-day English. In day-to-day English, there are two uses of the term "limit":
- Limit as something that one approaches, or is headed toward
- Limit as a boundary or cap that cannot be crossed or exceeded
The mathematical term "limit" refers to the first of these two meanings. In other words, the mathematical concept of limit is a formalization of the intuitive concept of limit as something that one approaches or is headed toward.
For a function  , the notation:
, the notation:

is meant to say "the limit, as  approaches
approaches  , of the function value
, of the function value  " and thus, the mathematical equality:
" and thus, the mathematical equality:

is meant to say "the limit, as  approaches
approaches  , of the function value
, of the function value  , is
, is  ." In a rough sense, what this means is that as
." In a rough sense, what this means is that as  gets closer and closer to
gets closer and closer to  ,
,  eventually comes, and stays, close enough to
eventually comes, and stays, close enough to  .
.
Graphical interpretation
The graphical interpretation of " " is that, if we move along the graph
" is that, if we move along the graph  of the function
of the function  in the plane, then the graph approaches the point
in the plane, then the graph approaches the point  whether we make
whether we make  approach
approach  from the left or the right. However, this interpretation works well only if
from the left or the right. However, this interpretation works well only if  is continuous on the immediate left and immediate right of
is continuous on the immediate left and immediate right of  .
.
This interpretation is sometimes termed the "two finger test" where one finger is used to follow the graph for  slightly less than
slightly less than  and the other finger is used to follow the graph for
and the other finger is used to follow the graph for  slightly greater than
slightly greater than  .
.
The interpretation is problematic in that it is not really a definition, and fails to have computational utility for wildly oscillatory functions or functions with other forms of weird behavior.
Two key ideas
The concept of limit involves two key ideas, both of which help explain why the definition is structured the way it is:
- Arbitrarily close: The limit depends on how things behave arbitrarily close to the point involved. The notion of "arbitrarily close" is difficult to quantify non-mathematically, but what it means is that any fixed distance is too much. For instance, if doing
 , we can take points close to 2 such as 2.1, 2.01, 2.001, 2.0001, 2.0000001, 2.000000000000001. Any of these points, viewed in and of itself, is too far from 2 to offer any meaningful information. It is only the behavior in the limit, as we get arbitrarily close, that matters.
, we can take points close to 2 such as 2.1, 2.01, 2.001, 2.0001, 2.0000001, 2.000000000000001. Any of these points, viewed in and of itself, is too far from 2 to offer any meaningful information. It is only the behavior in the limit, as we get arbitrarily close, that matters.
- Trapping of the function close by: For a function to have a certain limit at a point, it is not sufficient to have the function value come close to that point. Rather, for
 to hold, it is necessary that for
to hold, it is necessary that for  very close to
very close to  , the function value
, the function value  is trapped close to
is trapped close to  . It is not enough that it keeps oscillating between being close to
. It is not enough that it keeps oscillating between being close to  and being far from
and being far from  .
.
{{#widget:YouTube|id=iZ_fCNvYa9U}}
Full timed transcript: [SHOW MORE]
0:00:15.549,0:00:19.259
Vipul: Okay, so in this talk, I'm going to
go over the basic
0:00:19.259,0:00:24.619
motivation behind the definition of limit,
and not so much the
0:00:24.619,0:00:28.099
epsilon-delta definition. This is just an intuitive idea,
and a few somewhat
0:00:28.099,0:00:29.680
non-intuitive aspects of that.
0:00:29.680,0:00:36.680
Here I have the notation: "limit as x approaches
c of f(x) is L" is
0:00:37.540,0:00:42.079
written like this. Limit ... Under the limit,
we write where the
0:00:42.079,0:00:46.180
domain point goes, so x is approaching a value,
c, and c could be an
0:00:46.180,0:00:51.059
actual number. x, however, will always be
a variable letter. This x
0:00:51.059,0:00:54.519
will not be a number. c could be a number
like zero, one, two, three,
0:00:54.519,0:00:55.329
or something.
0:00:55.329,0:01:02.050
f(x). f is the function. We are saying that
as x approaches some
0:01:02.050,0:01:06.640
number c, f(x) approaches some number L, and
that's what this is:
0:01:06.640,0:01:09.030
Limit as x approaches c of f(x) is L.
0:01:09.030,0:01:15.259
Now what does this mean? Roughly what it means
is that as x is coming
0:01:15.259,0:01:22.259
closer and closer to c, f(x) is sort of hanging
around L. It's coming
0:01:22.410,0:01:28.720
closer and closer to L. By the way, there
are two senses in which the
0:01:28.720,0:01:32.429
word limit is used in the English language:
One meaning is limit in
0:01:32.429,0:01:36.310
this approach sense, which is the mathematical
meaning of limit.
0:01:36.310,0:01:41.319
There is another sense in which the word limit
is used in the English
0:01:41.319,0:01:46.220
language, which is limit as a boundary or as a cap or as a bound.
0:01:46.220,0:01:53.160
We may say, there is a limit to how many apples
you can eat from the
0:01:53.160,0:01:58.640
fruit bowl or something, and that sense of
limit is not used ... for
0:01:58.640,0:02:02.110
that sense of limit you do not use the word
"limit" in mathematics. For
0:02:02.110,0:02:05.899
that sense of limit, you use the word bound.
In mathematics, we
0:02:05.899,0:02:11.800
reserve the use of the word limit only for
this approach sense. Just
0:02:11.800,0:02:18.800
so we don't get confused in mathematics.
As I said, the idea is that
0:02:21.120,0:02:25.760
as x approaches c, f(x) approaches L, so as
x is coming closer and
0:02:25.760,0:02:29.480
closer to c, the distance between x and c
is becoming smaller and
0:02:29.480,0:02:32.740
smaller, the distance between f(x) and L is
also roughly becoming
0:02:32.740,0:02:37.980
smaller and smaller. This doesn't quite
work unless your function is
0:02:37.980,0:02:41.250
increasing or decreasing near c, so you could
have various
0:02:41.250,0:02:46.750
complications with oscillatory functions,
so the point is this notion
0:02:46.750,0:02:52.170
doesn't really ... it's not very clear what
we mean here without further
0:02:52.170,0:02:55.470
elaboration and without a clear definition.
0:02:55.470,0:03:02.470
I'm going to sort of move up toward the definition,
and before we go
0:03:02.970,0:03:09.180
there, I want to say, that there is a graphical
concept of limit,
0:03:09.180,0:03:13.430
which you may have seen in school. (well,
if you've seen limits in
0:03:13.430,0:03:17.110
school, which hopefully you have. This video
is sort of more of a
0:03:17.110,0:03:21.500
review type than learning it for the first
time). Let's try to
0:03:21.500,0:03:24.630
understand this from that point of view.
0:03:24.630,0:03:31.630
Let's say, you have a function whose graph
looks something like this.
0:03:35.990,0:03:42.990
This is x is c, so this is the value x is
c, and this is the graph of
0:03:44.069,0:03:48.310
the function, these curves are the graph of
the function, so where x
0:03:48.310,0:03:53.900
is less than c, the graph is along this curve.
For x greater than c,
0:03:53.900,0:03:58.120
the graph is this curve. So x less than c,
the graph is this curve; x
0:03:58.120,0:04:01.740
greater than c, the graph is this curve. At
x equal to c, the value
0:04:01.740,0:04:06.330
is that filled dot.
0:04:06.330,0:04:13.330
You can see from here that as x is approaching
c from the left, so if
0:04:13.880,0:04:17.819
you take values of x, which are slightly less
than c, the function
0:04:17.819,0:04:23.259
values ... so the function, the graph of it,
the function values are
0:04:23.259,0:04:27.449
their respective y coordinates, so this is
x, this is y, this is the
0:04:27.449,0:04:34.449
graph. y is f(x). When x is to the immediate
left of c, the value, y
0:04:35.749,0:04:42.749
value, the y equals f(x) value is ... are
these values, so this or
0:04:44.610,0:04:51.610
this. As x approaches c from the left, the
y values are approaching
0:04:53.699,0:04:57.240
the y coordinate of this open circle.
0:04:57.240,0:05:04.240
In a sense, if you just were looking at the
limit from the left for x
0:05:05.680,0:05:10.830
approaching c from the left, then the limit
would be the y coordinate
0:05:10.830,0:05:16.279
of this open circle. You can also see an x
approaches c from the
0:05:16.279,0:05:22.749
right, so approaches from here ... the y coordinate
is approaching the y
0:05:22.749,0:05:29.749
coordinate of this thing, this open circle
on top. There are actually
0:05:31.009,0:05:38.009
two concepts here, the left-hand limit
is this value. We will call
this L1. The right-hand limit is this value,
0:05:45.599,0:05:49.349
L2, so the left-hand
limit, which is the notation as limit as x
0:05:49.349,0:05:56.349
approaches c from the left
of f(x) is L1, the right-hand limit from the
0:05:58.089,0:06:05.089
right, that's plus of f(x),
is L2, and the value f of c is some third
0:06:08.059,0:06:15.059
number. We don't know what
it is, but f of c, L1, L2, are in this case
0:06:16.770,0:06:18.360
all different.
0:06:18.360,0:06:25.360
What does this mean as far as the limit is
concerned? Well, the
0:06:25.900,0:06:28.259
concept of limit is usually a concept of two
sided limit, which
0:06:28.259,0:06:33.419
means that in this case the limit as x approaches
c of f(x) does not
0:06:33.419,0:06:36.289
exist because you have a left-hand limit,
and you have a right-hand
0:06:36.289,0:06:39.860
limit, and they are not equal to each other.
The value, as such,
0:06:39.860,0:06:43.279
doesn't matter, so whether the value exists,
what it is, does not
0:06:43.279,0:06:46.379
affect this concept of limit, but the real
problem here is that the
0:06:46.379,0:06:48.490
left-hand limit and right-hand limit are not
equal. The left-hand
0:06:48.490,0:06:55.490
limit is here; the right-hand limit is up
here.
0:06:59.050,0:07:03.499
This graphical interpretation, you see the
graphical interpretation is
0:07:03.499,0:07:07.749
sort of that: for the left-hand limit, you
basically sort of follow
0:07:07.749,0:07:11.499
the graph on the immediate left and see where
it's headed to and you
0:07:11.499,0:07:15.789
get the y coordinate of that. For the right-hand
limit, you follow
0:07:15.789,0:07:21.129
the graph on the right and see where we're
headed to, and get the y
0:07:21.129,0:07:22.240
coordinate of that.
0:07:22.240,0:07:29.240
Let me make an example, where the limit does
exist. Let's say you
0:07:42.899,0:07:48.449
have a picture, something like this. In this
case, the left-hand limit
0:07:48.449,0:07:52.610
and right-hand limit are the same thing, so
this number, but the
0:07:52.610,0:07:55.889
value is different. You could also have
a situation where the value
0:07:55.889,0:08:00.460
doesn't exist at all. The function isn't
defined at the point, but
0:08:00.460,0:08:03.139
the limit still exists because the left-hand
limit and right-hand
0:08:03.139,0:08:04.719
limit are the same.
0:08:04.719,0:08:09.979
Now, all these examples, there's sort of a
crude way of putting this
0:08:09.979,0:08:13.710
idea, which is called the two-finger test.
You may have heard it in
0:08:13.710,0:08:18.399
some slightly different names. The two-finger
test idea is that you
0:08:18.399,0:08:23.929
use one finger to trace the curve on the immediate
left and see where
0:08:23.929,0:08:28.259
that's headed to, and use another finger
to trace the curve on the
0:08:28.259,0:08:33.640
immediate right and see where that's headed
to, and if your two
0:08:33.640,0:08:38.270
fingers can meet each other, then the place
where they meet, the y
0:08:38.270,0:08:41.870
coordinate of that, is the limit. If, however,
they do not come to
0:08:41.870,0:08:46.940
meet each other, which happens in this case,
one of them is here, one
0:08:46.940,0:08:51.120
is here, and then the limit doesn't exist
because the left-hand limit
0:08:51.120,0:08:53.509
and right-hand limit are not equal.
0:08:53.509,0:08:59.819
This, hopefully, you have seen in great detail
when you've done
0:08:59.819,0:09:05.779
limits in detail in school. However, what
I want to say here is that
0:09:05.779,0:09:11.850
this two-finger test is not really a good
definition of limit. What's
0:09:11.850,0:09:13.600
the problem? The problem is that you could
have really crazy
0:09:13.600,0:09:18.790
function, and it's really hard to move your
finger along the graph of
0:09:18.790,0:09:25.220
the function. If the function sort of jumps
around a lot, it's really
0:09:25.220,0:09:29.440
hard, and it doesn't really solve any problem.
It's not really a
0:09:29.440,0:09:35.100
mathematically pure thing. It's like trying
to answer the
0:09:35.100,0:09:39.540
mathematical question using a physical description,
which is sort of
0:09:39.540,0:09:41.579
the wrong type of answer.
0:09:41.579,0:09:45.610
While this is very good for a basic intuition
for very simple types of
0:09:45.610,0:09:50.040
functions, it's not actually the correct idea
of limit. What kind of
0:09:50.040,0:09:56.990
things could give us trouble? Why do we need
to refine our
0:09:56.990,0:10:03.209
understanding of limit? The main thing is
functions which have a lot
0:10:03.209,0:10:07.980
of oscillation. Let me do an example.
0:10:07.980,0:10:14.980
I'm now going to write down a type of function
where, in fact, you
0:10:18.220,0:10:21.899
have to develop a clear cut concept of limit
to be able to answer this
0:10:21.899,0:10:28.899
question precisely. This is a graph of a function,
sine 1 over x.
0:10:28.959,0:10:32.920
Now this looks a little weird. It's not 1
over sine x; that would
0:10:32.920,0:10:39.920
just equal cosecant x. It's not that. It's sine
of 1 over x, and this
0:10:44.879,0:10:50.220
function itself is not defined at x equals
zero, but just the fact
0:10:50.220,0:10:52.660
that that's not defined, isn't good enough
for us to say the limit
0:10:52.660,0:10:55.139
doesn't exist; we actually have
to try to make a picture
0:10:55.139,0:10:57.660
of this and try to understand what the limit
is going to be.
0:10:57.660,0:11:04.660
Let's first make the picture of sine x. Sine-x
looks like that. How
0:11:12.560,0:11:19.560
will sine 1 over x look? Let's start off where
x is nearly infinity.
0:11:20.100,0:11:25.759
When x is very large positive, 1 over x is
near zero, slightly
0:11:25.759,0:11:30.660
positive, just slightly bigger than zero,
and sine 1 over x is
0:11:30.660,0:11:36.879
therefore slightly positive. It's like here.
It's going to start off
0:11:36.879,0:11:42.810
with an asymptote, a horizontal asymptote, at zero.
Then it's going to sort of go
0:11:42.810,0:11:49.420
this path, but much more slowly, each one,
then it's going to go this
0:11:49.420,0:11:56.420
path, but in reverse, so like that. Then it's
going to go this path,
0:11:57.149,0:12:00.740
but now it does all these oscillations, all
of these oscillations. It
0:12:00.740,0:12:03.569
has to go faster and faster.
0:12:03.569,0:12:10.569
For instance, this is pi, this 1 over pi,
then this is 2 pi, this
0:12:12.329,0:12:16.990
number is 1 over 2 pi, then the then next
time it reaches zero will be
0:12:16.990,0:12:21.160
1 over 3 pi, and so on. What's going to
happen is that near zero it's
0:12:21.160,0:12:24.579
going to be crazily oscillating between minus
1, and 1. The frequency
0:12:24.579,0:12:29.170
of the oscillation keeps getting faster and
faster as you come closer
0:12:29.170,0:12:34.050
and closer to zero. The same type of picture
on the left side as
0:12:34.050,0:12:40.360
well; it's just that it's an odd function.
It's this kind of picture.
0:12:40.360,0:12:47.360
I'll make a bigger picture here ... I'll make
a bigger picture on another
0:12:53.649,0:13:00.649
one. all of these oscillation should be between
minus 1 and 1, and we
0:13:22.439,0:13:29.399
get faster so we get faster and faster, and
now my pen is too thick.
0:13:29.399,0:13:31.600
It's the same, even if you used your finger
instead of the pen to
0:13:31.600,0:13:38.600
place it, it would be too thick, it's called
the thick finger problem.
0:13:38.850,0:13:45.060
I'm not being very accurate here, but just
the idea. The pen or
0:13:45.060,0:13:49.199
finger is too thick, but actually, there's
a very thin line, and it's
0:13:49.199,0:13:52.519
an infinitely thin line of the graph, which
goes like that.
0:13:52.519,0:13:59.519
Let's get back to our question: What is limit
as x approaches zero,
0:14:02.699,0:14:09.699
sine 1 over x. I want you to think about this
a bit. Think about like
0:14:13.439,0:14:18.050
the finger test. You move your finger around,
move it like this,
0:14:18.050,0:14:21.579
this, this ... you're sort of getting close
to zero but still not quite
0:14:21.579,0:14:28.579
reaching it. It's ... where are you headed?
It's kind of a little
0:14:31.610,0:14:36.879
unclear. Notice, it's not that just because
we plug in zero doesn't
0:14:36.879,0:14:39.170
make sense, the limit doesn't... That's
not the issue. The issue is
0:14:39.170,0:14:43.249
that after you make the graph, it's unclear
what's happening.
0:14:43.249,0:14:49.329
One kind of logic is that, yeah, the limit
is zero? Why? Well, it's
0:14:49.329,0:14:52.949
kind of balanced around zero, right? It's a bit
above and below, and it keeps
0:14:52.949,0:14:59.949
coming close to zero. That any number of the
form x is 1 over N pi,
0:15:00.329,0:15:07.329
sine 1 over x is zero. It keeps coming close
to zero. As x
0:15:07.990,0:15:12.459
approaches zero, this number keeps coming
close to zero.
0:15:12.459,0:15:17.449
If you think of limit as something it's
approaching, then as x
0:15:17.449,0:15:24.449
approaches zero, sine 1 over x is sort of
coming close to zero, is it?
0:15:31.230,0:15:36.550
It's definitely coming near zero, right? Anything
you make around
0:15:36.550,0:15:41.920
zero, any small ... this you make around zero,
the graph is going to
0:15:41.920,0:15:42.399
enter that.
0:15:42.399,0:15:47.269
On the other hand, it's not really staying
close to zero. It's kind of
0:15:47.269,0:15:50.300
oscillating within [-1,1]. However
small an interval you
0:15:50.300,0:15:54.540
take around zero on the x thing, the function
is oscillating between
0:15:54.540,0:15:57.600
minus 1 and 1. It's not staying faithful to
zero.
0:15:57.600,0:16:02.249
Now you have kind of this question: What should
be the correct
0:16:02.249,0:16:09.249
definition of this limit? Should it mean that
it approaches the
0:16:10.029,0:16:15.100
point, but maybe goes in and out, close and
far? Or should it mean it
0:16:15.100,0:16:18.879
approaches and stays close to the point? That
is like a judgment you
0:16:18.879,0:16:22.629
have to make in the definition, and it so
happens that people who
0:16:22.629,0:16:28.639
tried defining this chose the latter idea;
that is, it should come
0:16:28.639,0:16:33.089
close and stay close. So that's actually
key idea number two we have
0:16:33.089,0:16:38.290
here the function ... for the function to
have a limit at the point, the
0:16:38.290,0:16:43.639
function needs to be trapped near the limit,
close to the point in the
0:16:43.639,0:16:45.079
domain.
0:16:45.079,0:16:49.459
This is, therefore, it doesn't have a limit
at zero because the
0:16:49.459,0:16:54.420
function is oscillating too widely. You cannot
trap it. You cannot
0:16:54.420,0:17:01.059
trap the function values. You cannot say that...
you cannot trap the
0:17:01.059,0:17:08.059
function value, say, in this small horizontal
strip near zero. You
0:17:08.319,0:17:11.650
cannot trap in the area, so that means the
limit cannot be zero, but
0:17:11.650,0:17:15.400
the same logic works anywhere else. The limit
cannot be half, because
0:17:15.400,0:17:20.440
you cannot trap the function in a small horizontal
strip about half
0:17:20.440,0:17:22.130
whereas x approaches zero.
0:17:22.130,0:17:26.440
We will actually talk about this example in
great detail in our future
0:17:26.440,0:17:30.330
with you after we've seen the formal definition,
but the key idea you
0:17:30.330,0:17:33.890
need to remember is that the function doesn't
just need to come close
0:17:33.890,0:17:37.340
to the point of its limit. It actually needs
to stay close. It needs
0:17:37.340,0:17:41.050
to be trapped near the point.
0:17:41.050,0:17:44.810
The other important idea regarding limits
is that the limit depends
0:17:44.810,0:17:50.370
only on the behavior very, very close to the
point. What do I mean by
0:17:50.370,0:17:56.580
very, very close? If you were working it like,
the real goal, you may
0:17:56.580,0:18:02.300
say, it's like, think of some really small
number and you say that
0:18:02.300,0:18:07.050
much distance from it. Let's say I want to
get the limit as x
0:18:07.050,0:18:14.050
approaches 2...I'll just write it here. I
want to get, let's say,
0:18:23.520,0:18:30.520
limit has x approaches 2 of some function,
we may say, well, we sort
0:18:30.550,0:18:37.550
of ... what's close enough? Is 2.1 close
enough? No, that's too far.
0:18:38.750,0:18:43.380
What about 2.0000001? Is that close enough?
0:18:43.380,0:18:47.420
Now, if you weren't a mathematician, you
would probably say, "Yes,
0:18:47.420,0:18:54.420
this is close enough." The difference is like
... so it's
0:18:57.040,0:19:04.040
10^{-7}. It's really only close to 2 compared
to our usual sense of
0:19:12.990,0:19:16.670
numbers, but as far as mathematics is concerned,
both of these numbers
0:19:16.670,0:19:21.110
are really far from 2. Any individual number
that is not 2 is very
0:19:21.110,0:19:22.130
far from 2.
0:19:22.130,0:19:29.130
What do I mean by that, well, think back to
one of our
0:19:29.670,0:19:36.670
pictures. Here's a picture. Supposed I take
some points. Let's say
0:19:41.970,0:19:47.640
this is 2, and suppose I take one point here,
which is really close to
0:19:47.640,0:19:50.970
2, and I just change the value of the function
at that point. I
0:19:50.970,0:19:55.200
change the value of the function at that point,
or I just change the
0:19:55.200,0:19:59.990
entire picture of the graph from that point
rightward. I just take
0:19:59.990,0:20:05.940
this picture, and I change it to, let's say
... so I replace this
0:20:05.940,0:20:11.410
picture by that picture, or I replace the
picture by some totally new
0:20:11.410,0:20:15.250
picture like that picture. I just change the
part of the graph to the
0:20:15.250,0:20:21.440
right of some point, like 2.00001, whatever.
Will that effect the
0:20:21.440,0:20:25.770
limit at 2? No, because the limit at 2 really
depends only on the
0:20:25.770,0:20:27.520
behavior if you're really, really close.
0:20:27.520,0:20:32.040
If you take any fixed point, which is not
2, and you change the
0:20:32.040,0:20:35.000
behavior, sort of at that point or
farther away than that
0:20:35.000,0:20:42.000
point, then the behavior close to 2 doesn't
get affected. That's the
0:20:42.820,0:20:46.660
other key idea here. Actually I did these
in reverse order.
0:20:46.660,0:20:52.060
That's how it was coming naturally, but I'll
just say it again.
0:20:52.060,0:20:56.570
The limit depends on the behavior arbitrarily
close to the point. It
0:20:56.570,0:21:00.210
doesn't depend on the behavior at any single
specific other point. It
0:21:00.210,0:21:06.910
just depends on the behavior as you approach
the point and any other
0:21:06.910,0:21:11.330
point is far away. It's only sort of together
that all the other
0:21:11.330,0:21:16.230
points matter, and it's only them getting
really close that
0:21:16.230,0:21:19.790
matters. The other thing is that the function
actually needs to be
0:21:19.790,0:21:26.790
trapped near the point for the limit notion
to be true. This type of
0:21:26.860,0:21:29.650
picture where it's oscillating between minus
1 and 1, however close
0:21:29.650,0:21:35.150
you get to zero, keeps oscillating, and so
you cannot trap it around
0:21:35.150,0:21:40.590
any point. You cannot trap the function value
in any small enough
0:21:40.590,0:21:47.590
strip. In that case, the limit doesn't exist.
In subsequent videos,
0:21:48.550,0:21:54.630
we'll see the epsilon delta definition, we'll do a bit
of formalism to that, and
0:21:54.630,0:22:00.640
then we'll come back to some of these issues
later with the formal
0:22:00.640,0:22:01.870
understanding.
Checkpoint questions:
- To figure out the limit of a function at
 , does the value of the function at
, does the value of the function at  matter? Does the value of the function at
matter? Does the value of the function at  matter?
matter?  ? How close is close enough?
? How close is close enough?
- What is the limit
 ? What's the intuitive idea behind the reasoning? More formal versions of this reasoning will be introduced after we have seen the
? What's the intuitive idea behind the reasoning? More formal versions of this reasoning will be introduced after we have seen the  definition.
definition.
Definition for finite limit for function of one variable
Two-sided limit
Suppose  is a function of one variable and
is a function of one variable and  is a point such that
is a point such that  is defined to the immediate left and immediate right of
is defined to the immediate left and immediate right of  (note that
(note that  may or may not be defined at
may or may not be defined at  ). In other words, there exists some value
). In other words, there exists some value  such that
such that  is defined on
is defined on  .
.
For a given value  , we say that:
, we say that:

if the following holds:
For every  , there exists
, there exists  such that for all
such that for all  satisfying
satisfying  , we have
, we have  .
.
The definition is broken down into its four clauses below:
| Clause |
Interval description |
Symbol explanations
|
For every  |
 |
The symbol  is a Greek lowercase letter pronounced "epsilon". is a Greek lowercase letter pronounced "epsilon".
Although the definition customarily uses the letter  , it can be replaced by any other letter, as long as the letter is different from the other letters in use. The reason for sticking to a standard letter choice is that it reduces cognitive overload. , it can be replaced by any other letter, as long as the letter is different from the other letters in use. The reason for sticking to a standard letter choice is that it reduces cognitive overload.
|
there exists  such that such that |
 |
The symbol  is a Greek lowercase letter pronounced "delta" is a Greek lowercase letter pronounced "delta"
Although the definition customarily uses the letter  , it can be replaced by any other letter, as long as the letter is different from the other letters in use. The reason for sticking to a standard letter choice is that it reduces cognitive overload. , it can be replaced by any other letter, as long as the letter is different from the other letters in use. The reason for sticking to a standard letter choice is that it reduces cognitive overload.
|
for all  satisfying satisfying  |
 |
The symbol  stands for the absolute value function. stands for the absolute value function.
 stands for "is in the set" so the statements should be read as saying that stands for "is in the set" so the statements should be read as saying that  is in the set described in the two equivalent ways. is in the set described in the two equivalent ways.
 stands for the union, so the statement that stands for the union, so the statement that  should be parsed as saying that should be parsed as saying that  or or 
 stands for set difference, so the statement stands for set difference, so the statement  can be parsed as saying that can be parsed as saying that  could be any value in could be any value in  except except  . The point . The point  is excluded because we do not want the value of is excluded because we do not want the value of  at at  to affect the limit notion. to affect the limit notion.
|
we have  |
 |
The symbol  stands for the absolute value function. stands for the absolute value function.
 stands for "is in the set" so the statement should be read as saying that stands for "is in the set" so the statement should be read as saying that  is in the set is in the set  . .
|
The limit (also called the two-sided limit)  is defined as a value
is defined as a value  such that
such that  . By the uniqueness theorem for limits, there is at most one value of
. By the uniqueness theorem for limits, there is at most one value of  for which
for which  . Hence, it makes sense to talk of the limit when it exists.
. Hence, it makes sense to talk of the limit when it exists.
{{#widget:YouTube|id=0vy0Fslxi-k}}
Full timed transcript: [SHOW MORE]
0:00:15.809,0:00:20.490
Vipul: In this talk, I'm going to introduce
the definition, the formal epsilon delta definition
0:00:20.490,0:00:24.669
of a two-sided limit for a function of a one
variable, that's called f.
0:00:24.669,0:00:31.349
I'm going to assume there is a point c and c
doesn't actually have to be in the domain of f.
0:00:31.349,0:00:38.030
Thus f doesn't have to be defined at c for this notion to
make sense rather f is defined around c.
0:00:38.030,0:00:44.909
What that means is f is defined on some open
set containing c.
0:00:51.009,0:01:03.009
Let's make a picture here so you have c,
c + t, c -- t.
0:01:03.040,0:01:11.040
What this is saying is there is some t probably
small enough so that the function is defined
0:01:12.549,0:01:18.590
in here and may be it's not defined at the
point c.
0:01:18.590,0:01:31.590
This set for some t>0. The function is defined
on the immediate left of c and it is defined
0:01:31.999,0:01:34.770
on the immediate right of c.
0:01:34.770,0:01:38.890
We need that in order to make sense of what
I'm going to say.
0:01:38.890,0:01:44.590
We say that limit as x approaches c of f(x)
is L where L is some other real number or
0:01:44.590,0:01:49.679
maybe it's the same real number [as c], so we say
this limit equals L, now I'll write the definition
0:01:49.679,0:01:56.679
in multiple lines just to be clear about the
parts of the definition.
0:01:56.770,0:02:39.770
For every epsilon > 0. This is epsilon. There
exists delta > 0 such that
for all x in R satisfying...what?
0:02:41.070,0:02:45.070
Rui: Satisfying |x -- c| ...
0:02:45.659,0:02:53.659
Vipul: [|x-c|] should be not equal to zero so zero
less than, exclude the point c itself,
0:02:54.810,0:02:56.930
less than delta. What do we have?
0:02:56.930,0:02:59.459
Rui: We have y is within.
0:02:59.459,0:03:04.260
Vipul: Well y is just f(x).
0:03:04.260,0:03:10.290
Rui: f(x_0)
0:03:14.290,0:03:16.819
Vipul: Well f(x) minus the claimed limit is?
0:03:17.219,0:03:18.040
Rui: L.
0:03:18.640,0:03:22.890
Vipul: You're thinking of continuity which is a
little different but here we have this less than?
0:03:22.890,0:03:24.569
Rui: Epsilon.
0:03:24.569,0:03:37.569
Vipul: Epsilon. Let me now just re-write these
conditions in interval notation.
0:03:37.830,0:03:40.031
What is this saying x in what interval? [ANSWER!]
0:03:40.040,0:03:43.519
Rui: c +- ...
0:03:43.519,0:03:49.840
Vipul: c- delta to c + delta excluding the
point c itself, that is what 0 < [|x -- c|] is telling us.
0:03:49.840,0:03:56.530
It is telling us x is within delta distance
of c, but it is not including c.
0:03:56.530,0:04:10.530
Another way of writing this is (c -- delta,c) union (c, c + delta)
0:04:12.810,0:04:19.340
x is either on immediate delta left of c or
it's on the immediate delta right of c.
0:04:21.040,0:04:31.040
You do something similar on the f(x) side
so what interval is this saying, f(x) is in what? [ANSWER!]
0:04:31.720,0:04:35.930
Rui: L -- epsilon, L + epsilon.
0:04:35.930,0:04:42.930
Vipul: Awesome. Instead of writing the conditions
in this inequality form you could have written
0:04:43.919,0:04:47.590
them in this form, so instead of writing this
you could have written this or this, instead
0:04:47.590,0:04:49.580
of writing this you could have written this.
0:04:50.080,0:04:59.500
If this statement is true, the way you read this is you say
limit as x approaches c of f(x) equals L.
0:04:59.500,0:05:07.500
Okay. Now how do we define the limit?
0:05:11.169,0:05:18.169
It's the number L for which the above holds. This should be
in quotes.
0:05:22.009,0:05:29.009
If a number L exists for which.
0:05:34.220,0:05:41.220
Now what would you need in order to show that
this definition makes sense?
0:05:47.919,0:05:52.919
Rui: I don't think I understand your question.
0:06:03.090,0:06:09.090
Vipul: What I mean is, what I wanted to ask
was what would you need to prove in order
0:06:09.990,0:06:14.889
to say the notion of the limit makes sense? Well,
you need to show that there is uniqueness here.
0:06:14.740,0:06:19.080
It cannot happen that the limit is some number
L and the limit is another number M so you
0:06:19.080,0:06:20.539
need to show uniqueness.
0:06:20.539,0:06:27.330
You need to show that if this holds for one
number L it cannot also hold for another number.
0:06:27.330,0:06:32.050
Once you have shown that then it you could
define it like this.
0:06:32.050,0:06:38.440
Now I should say "if it exists."
0:06:38.440,0:06:42.120
What I'm saying is that there is a uniqueness
theorem which we will prove some other time.
0:06:42.120,0:06:49.120
Which says that if this is true for one number
it cannot be true for any other number so
0:06:49.440,0:06:54.740
this statement is true for at the most one
value of L and if there is such a value of
0:06:54.740,0:06:55.050
L that's called the limit.
Checkpoint questions:
- In order to make sense of
 where must the function
where must the function  be defined? Must
be defined? Must  be defined at
be defined at  ? If
? If  exists, what can we say about its value?
exists, what can we say about its value?
- What's the formal definition of limit, i.e., what does
 mean?
mean?
- How would you write the formal definition of limit using intervals rather than absolute value inequalities to describe where
 and
and  should be?
should be?
- Why is there a "
 " in the inequality
" in the inequality  in the
in the  definition? Why doesn't a
definition? Why doesn't a  appear in the
appear in the  part of the definition?
part of the definition?
- In order to be able to talk of the limit
 , what additional fact do we need beyond the definition of what
, what additional fact do we need beyond the definition of what  means?
means?
Left-hand limit
Suppose  is a function of one variable and
is a function of one variable and  is a point such that
is a point such that  is defined on the immediate left of
is defined on the immediate left of  (note that
(note that  may or may not be defined at
may or may not be defined at  ). In other words, there exists some value
). In other words, there exists some value  such that
such that  is defined on
is defined on  .
.
For a given value  , we say that:
, we say that:

if the following holds:
For every  , there exists
, there exists  such that for all
such that for all  satisfying
satisfying  , we have
, we have  .
.
The definition is broken down into its four clauses below:
| Clause |
Interval description |
Symbol explanations
|
For every  |
 |
The symbol  is a Greek lowercase letter pronounced "epsilon". is a Greek lowercase letter pronounced "epsilon".
Although the definition customarily uses the letter  , it can be replaced by any other letter, as long as the letter is different from the other letters in use. The reason for sticking to a standard letter choice is that it reduces cognitive overload. , it can be replaced by any other letter, as long as the letter is different from the other letters in use. The reason for sticking to a standard letter choice is that it reduces cognitive overload.
|
there exists  such that such that |
 |
The symbol  is a Greek lowercase letter pronounced "delta" is a Greek lowercase letter pronounced "delta"
Although the definition customarily uses the letter  , it can be replaced by any other letter, as long as the letter is different from the other letters in use. The reason for sticking to a standard letter choice is that it reduces cognitive overload. , it can be replaced by any other letter, as long as the letter is different from the other letters in use. The reason for sticking to a standard letter choice is that it reduces cognitive overload.
|
for all  satisfying satisfying  |
 |
The symbol  stands for the absolute value function. stands for the absolute value function.
 stands for "is in the set" so the statements should be read as saying that stands for "is in the set" so the statements should be read as saying that  is in the set is in the set  describing the immediate describing the immediate  -left of -left of  . .
|
we have  |
 |
The symbol  stands for the absolute value function. stands for the absolute value function.
 stands for "is in the set" so the statement should be read as saying that stands for "is in the set" so the statement should be read as saying that  is in the set is in the set  . .
|
The left-hand limit (acronym LHL)  is defined as a value
is defined as a value  such that
such that  . By the uniqueness theorem for limits (one-sided version), there is at most one value of
. By the uniqueness theorem for limits (one-sided version), there is at most one value of  for which
for which  . Hence, it makes sense to talk of the left hand limit when it exists.
. Hence, it makes sense to talk of the left hand limit when it exists.
Right-hand limit
Suppose  is a function of one variable and
is a function of one variable and  is a point such that
is a point such that  is defined on the immediate right of
is defined on the immediate right of  (note that
(note that  may or may not be defined at
may or may not be defined at  ). In other words, there exists some value
). In other words, there exists some value  such that
such that  is defined on
is defined on  .
.
For a given value  , we say that:
, we say that:

if the following holds:
For every  , there exists
, there exists  such that for all
such that for all  satisfying
satisfying  , we have
, we have  .
.
The definition is broken down into its four clauses below:
| Clause |
Interval description |
Symbol explanations
|
For every  |
 |
The symbol  is a Greek lowercase letter pronounced "epsilon". is a Greek lowercase letter pronounced "epsilon".
Although the definition customarily uses the letter  , it can be replaced by any other letter, as long as the letter is different from the other letters in use. The reason for sticking to a standard letter choice is that it reduces cognitive overload. , it can be replaced by any other letter, as long as the letter is different from the other letters in use. The reason for sticking to a standard letter choice is that it reduces cognitive overload.
|
there exists  such that such that |
 |
The symbol  is a Greek lowercase letter pronounced "delta" is a Greek lowercase letter pronounced "delta"
Although the definition customarily uses the letter  , it can be replaced by any other letter, as long as the letter is different from the other letters in use. The reason for sticking to a standard letter choice is that it reduces cognitive overload. , it can be replaced by any other letter, as long as the letter is different from the other letters in use. The reason for sticking to a standard letter choice is that it reduces cognitive overload.
|
for all  satisfying satisfying  |
 |
The symbol  stands for the absolute value function. stands for the absolute value function.
 stands for "is in the set" so the statements should be read as saying that stands for "is in the set" so the statements should be read as saying that  is in the set is in the set  describing the immediate describing the immediate  -right of -right of  . .
|
we have  |
 |
The symbol  stands for the absolute value function. stands for the absolute value function.
 stands for "is in the set" so the statement should be read as saying that stands for "is in the set" so the statement should be read as saying that  is in the set is in the set  . .
|
The right-hand limit (acronym RHL)  is defined as a value
is defined as a value  such that
such that  . By the uniqueness theorem for limits (one-sided version), there is at most one value of
. By the uniqueness theorem for limits (one-sided version), there is at most one value of  for which
for which  . Hence, it makes sense to talk of the right hand limit when it exists.
. Hence, it makes sense to talk of the right hand limit when it exists.
Side-by-side comparison of the definitions
Clause for two-sided limit  |
Clause for left hand limit  |
Clause for right hand limit  |
Comments
|
For every  |
For every  |
For every  |
identical so far
|
there exists  such that such that |
there exists  such that such that |
there exists  such that such that |
still identical
|
for all  satisfying satisfying  , i.e., , i.e.,  |
for all  satisfying satisfying  , i.e., , i.e.,  |
for all  satisfying satisfying  , i.e., , i.e.,  |
this is the part that differs, in so far as it is the direction of domain approach that differs between the definitions.
|
we have  , i.e., , i.e.,  |
we have  , i.e., , i.e.,  |
we have  , i.e., , i.e.,  |
this part is again identical. Note that the left versus right is only about the direction of approach in the domain, not about the direction of approach of the function value.
|
{{#widget:YouTube|id=qBjqc78KGx0}}
Full timed transcript: [SHOW MORE]
0:00:15.940,0:00:20.740
Vipul: In this talk, I'm going to give definitions
of one-sided limits.
0:00:20.740,0:00:25.650
So it is going to be the left hand limit and
the right hand limit, and I'm going to basically
0:00:25.650,0:00:42.650
compare it with the definition of two-sided limit which was in
a previous video. Let's just write this down--left-hand limit.
0:00:44.110,0:00:48.679
Let me first remind you what the definition
of two-sided limit says.
0:00:48.679,0:00:57.679
So here's what it says. It says limit as x approaches
c, f(x) = L
0:00:58.469,0:01:03.140
so f has to be defined on the immediate left and
the immediate right of c.
0:01:03.140,0:01:07.960
It says that this is true if the following
holds so for every epsilon greater than zero
0:01:07.960,0:01:13.960
there exists a delta > 0 such that for all
x which are within delta of c
0:01:14.000,0:01:22.771
either delta on the left of c or within a delta on the
right of c we have that f(x) is within an epsilon
0:01:23.650,0:01:30.530
distance of L.
Okay. Now with the left and right hand limit
0:01:30.530,0:01:37.460
what we are trying to do we are trying to
consider only one-sided approaches on the, on the x
0:01:39.000,0:01:41.510
What will change when we do the left-hand limit,
0:01:42.001,0:01:44.641
what will be different from this definition?
[ANSWER!]
0:01:45.710,0:01:48.330
Rui: We approach c from the left.
0:01:48.330,0:01:52.790
Vipul: We'll approach c from the left so
what part of this definition will change? [ANSWER!]
0:01:52.790,0:01:54.880
Rui: From the fourth line?
0:01:54.880,0:01:56.890
Vipul: You mean this line?
0:01:56.890,0:02:06.810
Rui: Oh for all x within c distance, within delta distance of c
0:02:06.810,0:02:08.700
Vipul: So what will change?
0:02:08.700,0:02:14.020
Rui: We will not have (c, c + delta).
0:02:14.020,0:02:18.390
Vipul: This part won’t be there. We will
just be concerned about whether when x is
0:02:18.390,0:02:23.000
delta close on the left side of c, f(x) is here...
0:02:23.000,0:02:28.000
Will we change this one also to only include the left? [ANSWER!]
0:02:28.000,0:02:30.000
Or this one will remain as it is?
0:02:30.300,0:02:31.500
Rui: I think it will remain.
0:02:31.500,0:02:33.460
Vipul: It will remain as it is because we
0:02:33.460,0:02:35.340
are just saying as x approaches c from the left
0:02:35.340,0:02:36.340
f(x) approaches L.
0:02:36.340,0:02:43.340
We are not claiming that f(x) approaches L
from the left, okay? Let me make a number line picture.
0:02:51.750,0:02:56.130
We will do a full geometric understanding
of the thing later. Right now it's just very [formal].
0:02:56.130,0:03:00.850
So the function is defined on the immediate left
of c, maybe not defined at c. It is defined
0:03:00.850,0:03:01.920
on the immediate left of c.
0:03:01.920,0:03:06.410
We don’t even know if the function
is defined on the right of c and what we are
0:03:06.410,0:03:13.410
saying is that for any epsilon, so any epsilon
around L you can find a delta such that if you restrict
0:03:13.800,0:03:20.800
attention to the interval from c minus delta
to c [i.e., (c- delta, c) in math notation]
0:03:21.450,0:03:23.130
then the f value there is within the epsilon distance of L.
0:03:24.130,0:03:28.959
Now the f value could be epsilon to the left
or the right so we take left hand limit on
0:03:28.959,0:03:33.840
the domain side it doesn’t have to approach
from the left on the other side.
0:03:33.840,0:03:40.690
Let me just write down the full definition. We want to keep this on the side.
0:03:40.690,0:04:03.690
What it says that for every epsilon > 0 there
exists
0:04:05.180,0:04:16.680
by the way, the understanding of the what this definition
really means will come in another video you may have seen before this or after this
0:04:16.680,0:04:21.209
... for all x ... [continuing definition]
0:04:21.209,0:04:26.500
Now we should also change it if we are writing
in this form so how will it read now?
0:04:26.500,0:04:28.030
Rui: For all x ...
0:04:35.000,0:04:38.000
Vipul: So will you put x – c or c – x? [ANSWER!]
0:04:38.330,0:04:40.990
Rui: It will be x – c, oh c – x.
0:04:41.000,0:04:46.760
Vipul: c – x. Because you want c to be bigger
than x. You want x to be on the left of c.
0:04:46.850,0:05:01.850
What would this read, i.e. x is in (c – delta,c).
Okay.
0:05:05.000,0:05:11.460
What do we have? We have the same thing. This part doesn’t change.
0:05:13.000,0:05:19.000
Rui: f(x) is within epsilon distance of L.
0:05:34.400,0:05:40.400
Vipul: Why do I keep saying this thing about the
L approach doesn’t have to be from the left?
0:05:41.000,0:05:44.350
What’s the significance of that? Why is that important?
[ANSWER!]
0:05:45.000,0:05:51.000
Rui: It’s important because we don’t know
whether the function is decreasing or increasing
0:05:51.620,0:05:52.370
at that point.
0:05:52.370,0:05:55.750
Vipul: Yeah, so if your function is actually
increasing than L will also be approached
0:05:55.750,0:06:01.590
from the left, and if it’s decreasing it
will be approached from the right, but sometimes
0:06:01.590,0:06:07.590
it’s neither increasing nor decreasing, but it's still
true it approaches from one side, so that’s a
little complicated but the way
0:06:07.590,0:06:12.150
this comes up is that when you are dealing
with composition of functions, so when you
0:06:12.150,0:06:16.710
are doing one function and then applying another function to that and you have some results
0:06:16.710,0:06:18.440
with one-sided limits.
0:06:18.440,0:06:30.440
Let me just write this down. If you have one-sided
limits and you have composition,
0:06:31.610,0:06:39.550
so you are doing one function and then doing another
you have to be very careful.
0:06:45.050,0:06:48.350
You need to be very careful when you are doing
one-sided limits and composition.
0:06:48.360,0:06:57.360
Why? Because if you have g of f(x) and x approaches
to c from the left, f(x) approaches L but
0:06:57.850,0:06:59.280
not necessarily from the left.
0:06:59.280,0:07:03.560
You then you have another thing which is as
f(x) approaches L from the left, g of that
0:07:03.560,0:07:09.280
approaches something you just need to be careful
that when you compose things the sidedness
0:07:09.280,0:07:10.930
could change each time you compose.
0:07:10.930,0:07:14.590
Rui: Can you write a composition of the function
out?
0:07:14.590,0:07:17.870
Vipul: Not in this video. We will do that
in another video.
0:07:17.870,0:07:23.800
That’s something we will see in a subsequent
video but this is just something to keep in
0:07:23.800,0:07:27.770
mind so when you see that it will ring a bell.
0:07:30.770,0:07:31.880
Let us do... what other side is left? [pun unintended!]
Rui: Right?
Vipul: Right!
0:07:31.880,0:07:36.690
Vipul: By the way, you probably already know
this if you have seen limits intuitively so
0:07:36.690,0:07:42.300
I'm not stressing this too much but left hand
limit is really the limit as you approach
0:07:42.300,0:07:49.300
from the left. You are not moving toward the
left you are moving from the left to the point.
0:07:50.160,0:07:55.940
Right hand limit will be approach from the
right to the point so it is right, moving from
0:07:55.940,0:07:59.330
the right, so the words left and right are
describing where the limit is coming *from*,
0:07:59.330,0:08:06.330
not the direction which it is going to.
0:08:12.569,0:08:17.650
Now you can just tell me what will be the
corresponding thing. To make sense of this
0:08:17.650,0:08:19.819
notion we need f to be defined where? [ANSWER!]
0:08:19.819,0:08:21.699
Rui: On its right.
0:08:21.699,0:08:29.199
Vipul: On the immediate right of c. If it
is not defined on the immediate right it doesn’t
0:08:29.389,0:08:36.389
even make sense to ask this question what
the right hand limit is.
0:08:37.280,0:08:38.550
How will that be defined?
0:08:38.550,0:08:44.240
Rui: For every epsilon greater than zero
0:08:44.240,0:08:51.240
Vipul: The epsilon is the interval on which
you are trying to trap the function value.
0:08:51.500,0:08:54.279
Rui: There exists epsilon
0:08:54.279,0:08:55.890
Vipul: No, delta
0:08:55.890,0:09:14.890
Rui: delta> 0 such that for all x
with x – c > 0
0:09:15.040,0:09:22.040
Vipul: The general one is for all x with 0<|x-c|<delta
because you want to capture both the intervals.
0:09:23.170,0:09:29.270
In this one, the left hand limit one, we just
captured the left side interval.
0:09:29.270,0:09:39.270
Now in the right one we just want to capture
the right side interval, so as you said 0< x- c < delta.
0:09:44.180,0:09:51.480
In the picture, the function is defined, say c
to c + t and you are really saying you can
0:09:52.290,0:10:00.290
find delta if x is in here [between c and c + delta] which
actually... this is not including c, it is all the points
0:10:00.390,0:10:05.390
in the immediate right of c. We have? [ANSWER!]
0:10:06.000,0:10:13.000
Rui: The absolute value of f(x) – L is less
than epsilon.
0:10:20.010,0:10:22.010
Vipul: So f(x) is? Are we here? We have everything?
0:10:23.010,0:10:23.260
Rui: Yes.
0:10:26.190,0:10:30.890
Vipul: We have both of these here? So do you
see what’s the main difference between these
0:10:30.890,0:10:37.430
two and the actual [two-sided limit] definition?
0:10:37.430,0:10:42.930
For every epsilon there exists delta... the
first second and fourth line remain the same.
0:10:42.930,0:10:47.440
It is this line where you are specifying where
the x are that’s different.
0:10:47.440,0:10:53.000
In the two-sided thing the x could be either place.
0:10:53.300,0:10:55.200
For the left hand limit the x,
0:10:55.720,0:10:59.000
you just want x here [in (c - delta, c)] and
0:10:59.000,0:11:07.000
for the right hand limit you just want x in (c,c + delta).
0:11:07.000,0:11:09.000
Okay? [END!]
Checkpoint questions:
- In order to make sense of
 , where must the function
, where must the function  be defined? Must
be defined? Must  be defined at
be defined at  ? If
? If  exists, what can we say about its value?
exists, what can we say about its value?
- The definitions of left hand limit, right hand limit and ordinary (two-sided) limit are pretty similar. There is only one clause that differs across the three definitions. What clause is this, and how does it differ across the definitions? Explain both in inequality notation and in interval notation.
- Why should we be careful when dealing with one-sided limits in the context of function compositions?
Relation between the limit notions
The two-sided limit exists if and only if (both the left hand limit and right hand limit exist) and (they are equal to each other).
Explicitly,  exists if all three of these conditions hold:
exists if all three of these conditions hold:
 exists.
exists. exists.
exists. .
.
Moreover, in the event that both one-sided limits exist and are equal, the two-sided limit is equal to both of them.
Further, a particular value of  works for a particular value of
works for a particular value of  in the two-sided limit definition if and only if it works in both the left hand limit definition and the right hand limit definition.
in the two-sided limit definition if and only if it works in both the left hand limit definition and the right hand limit definition.
Definition of finite limit for function of one variable in terms of a game
The formal definitions of limit, as well as of one-sided limit, can be reframed in terms of a game. This is a special instance of an approach that turns any statement with existential and universal quantifiers into a game.
Two-sided limit
Consider the limit statement, with specified numerical values of  and
and  and a specified function
and a specified function  :
:

Note that there is one trivial sense in which the above statement can be false, or rather, meaningless, namely, that  is not defined on the immediate left or immediate right of
is not defined on the immediate left or immediate right of  . In that case, the limit statement above is false, but moreover, it is meaningless to even consider the notion of limit. We therefore omit this sense from consideration and consider instead only the situation where
. In that case, the limit statement above is false, but moreover, it is meaningless to even consider the notion of limit. We therefore omit this sense from consideration and consider instead only the situation where  is defined on the immediate left and immediate right of
is defined on the immediate left and immediate right of  .
.
The game is between two players, a Prover whose goal is to prove that the limit statement is true, and a Skeptic (also called a Verifier or sometimes a Disprover) whose goal is to show that the statement is false. The game has three moves:
- First, the skeptic chooses
 , or equivalently, chooses the target interval
, or equivalently, chooses the target interval  in which the skeptic is challenging the prover to trap the function.
in which the skeptic is challenging the prover to trap the function.
- Then, the prover chooses
 , or equivalently, chooses the interval
, or equivalently, chooses the interval  .
.
- Then, the skeptic chooses a value
 satisfying
satisfying  , or equivalently,
, or equivalently,  , which is the same as
, which is the same as  .
.
Now, if  (i.e.,
(i.e.,  ), the prover wins. Otherwise, the skeptic wins.
), the prover wins. Otherwise, the skeptic wins.
We say that the limit statement

is true if the prover has a winning strategy for this game. The winning strategy for the prover basically constitutes a strategy to choose an appropriate  in terms of the
in terms of the  chosen by the skeptic. Thus, it is an expression of
chosen by the skeptic. Thus, it is an expression of  as a function of
as a function of  . Verbally, the goal of the prover is to choose a value of
. Verbally, the goal of the prover is to choose a value of  so that when the input is restricted to being within
so that when the input is restricted to being within  distance of
distance of  , the output is trapped to within
, the output is trapped to within  distance of the claimed limit
distance of the claimed limit  .
.
We say that the limit statement

is false if the skeptic has a winning strategy for this game. The winning strategy for the skeptic involves a choice of  , and a strategy that chooses a value of
, and a strategy that chooses a value of  (constrained in the specified interval) based on the prover's choice of
(constrained in the specified interval) based on the prover's choice of  .
.
Let's review the definition in conjunction with the game along with a deeper semantic understanding of the steps:
| Step no. |
Clause of definition |
Who moves? |
What is chosen? |
Constraints on the choice |
Comment
|
| 1 |
For every  |
Skeptic |
 |
Must be positive |
The "for every" corresponds to the idea that the move is made by the side that does not have a winning strategy, because we want to argue that the side that does have a winning strategy can win no matter what.
|
| 2 |
there exists  such that such that |
Prover |
 |
Must be positive |
The "there exists" corresponds to the idea that the move is made by the side that has a winning strategy, because that side gets to choose a favorable value of the variable (in this case  ). ).
|
| 3 |
for all  satisfying satisfying  , , |
Skeptic |
 |
Must be within the interval  |
The "for all" corresponds to the idea that the move is made by the side that does not have a winning strategy, because we want to argue that the side that does have a winning strategy can win no matter what.
|
| 4 |
we have  |
Neither; it's time for the judge to decide |
-- |
If  (the condition that we desire) the prover wins. Else, the skeptic wins. (the condition that we desire) the prover wins. Else, the skeptic wins. |
|
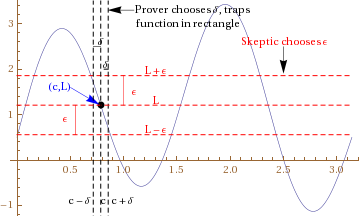
Slight subtlety regarding domain of definition: [SHOW MORE]
The domain of definition issue leads to a couple of minor subtleties:
- A priori, it is possible that the
 chosen by the skeptic is outside the domain of
chosen by the skeptic is outside the domain of  , so it does not make sense to evaluate
, so it does not make sense to evaluate  . In the definition given above, this would lead to the game being won by the skeptic. In particular, if
. In the definition given above, this would lead to the game being won by the skeptic. In particular, if  is not defined on the immediate left or right of
is not defined on the immediate left or right of  , the skeptic can always win by picking
, the skeptic can always win by picking  outside the domain.
outside the domain.
- It may make sense to restrict discussion to the cases where
 is defined on the immediate left or right of
is defined on the immediate left or right of  . Explicitly, we assume that
. Explicitly, we assume that  is defined on the immediate left and immediate right, i.e., there exists
is defined on the immediate left and immediate right, i.e., there exists  such that
such that  is defined on the interval
is defined on the interval  . In this case, it does not matter what rule we set regarding the case that the skeptic picks
. In this case, it does not matter what rule we set regarding the case that the skeptic picks  outside the domain. To simplify matters, we could alter the rules in any one of the following ways, and the meaning of limit would remain the same as in the original definition:
outside the domain. To simplify matters, we could alter the rules in any one of the following ways, and the meaning of limit would remain the same as in the original definition:
- We could require (as part of the game rules) that the prover pick
 such that
such that  . This pre-empts the problem of picking
. This pre-empts the problem of picking  -values outside the domain.
-values outside the domain.
- We could require (as part of the game rules) that the skeptic pick
 in the domain, i.e., pick
in the domain, i.e., pick  with
with  and
and  .
.
- We could alter the rule so that if the skeptic picks
 outside the domain, the prover wins (instead of the skeptic winning).
outside the domain, the prover wins (instead of the skeptic winning).
Full timed transcript: [SHOW MORE]
0:00:15.589,0:00:21.160
Vipul: In this video, I'm going to go over
the usual definition of limit and think of
0:00:21.160,0:00:24.930
it in terms of a game.
0:00:24.930,0:00:26.390
The game is as follows.
0:00:26.390,0:00:27.340
Consider this statement.
0:00:27.340,0:00:31.509
You are saying limit as x approaches c of
f(x) is L.
0:00:31.509,0:00:32.029
Okay.
0:00:32.029,0:00:35.160
There are two players to this game.
0:00:35.160,0:00:38.600
One is the prover and one is the skeptic.
0:00:38.600,0:00:44.550
The prover's goal is to show that this claim
is true so the prover is trying to convince
0:00:44.550,0:00:48.730
the skeptic that this limit as x approaches
c of f(x) is L,
0:00:48.730,0:01:01.160
the skeptic will try to ask tough questions and
see if the prover can still manage to show this.
0:01:01.160,0:01:04.059
The way the game is structured is as follows.
0:01:04.059,0:01:08.899
Let me just go over the individual components
of the statement for the limit and I will
0:01:08.899,0:01:10.610
translate each one.
0:01:10.610,0:01:17.610
I will explain the game and then explain how
it corresponds to the definition you've seen.
0:01:20.219,0:01:27.219
We begin with the skeptic
chooses epsilon > 0.
0:01:35.840,0:01:42.840
This is the part of the definition which reads
for every epsilon > 0.
0:01:47.099,0:01:53.289
That's the first clause of the definition
and that's basically the skeptic is choosing
0:01:53.289,0:01:54.579
epsilon > 0.
0:01:54.579,0:01:59.299
What is the skeptic trying to do when choosing
epsilon > 0?
0:01:59.299,0:02:06.299
What the skeptic is effectively doing is choosing
this interval L -- epsilon to L + epsilon.
0:02:14.400,0:02:18.220
The skeptic is effectively trying to choose
this interval L -- epsilon to L + epsilon.
0:02:18.220,0:02:26.110
What is the skeptic trying the challenge the prover
into doing when picking this interval? [ANSWER!]
0:02:26.110,0:02:29.890
Rui: Whether the prover can trap.
0:02:29.890,0:02:35.180
Vipul: The skeptic is trying to challenge
(and this will become a clearer a little later).
0:02:35.180,0:02:41.790
The idea is, the skeptic is trying to challenge
the prover into trapping the function when
0:02:41.790,0:02:47.620
the input x is close to c, trapping the
function output within this interval and that's
0:02:47.620,0:02:52.459
not clear which is why we need to continue
its definition.
0:02:52.459,0:02:58.609
The prover chooses. What does the prover choose?
[ANSWER!]
0:02:58.609,0:03:00.260
Rui: delta.
0:03:00.260,0:03:07.260
Vipul: delta > 0 and this corresponds to the
next part of the definition which says
0:03:08.480,0:03:15.480
there exists delta > 0.
0:03:19.749,0:03:26.749
In this picture, which I have up here, this
is the value c.
0:03:28.840,0:03:31.989
This is c + delta and this is c -- delta.
0:03:31.989,0:03:41.349
This is c and L, so c is the x coordinate, L is
the function value or limited the function value.
0:03:41.349,0:03:48.349
The skeptic chooses this strip like this from
L -- epsilon to L + epsilon by choosing epsilon
0:03:51.450,0:03:56.109
so the skeptic just chooses the number absent
what it is effectively doing is to choose
0:03:56.109,0:04:01.790
this strip, L -- epsilon to L + epsilon.
The prover then chooses a delta.
0:04:01.790,0:04:03.829
What's the prover effectively choosing?
0:04:03.829,0:04:07.290
The prover is effectively choosing this interval.
0:04:07.290,0:04:14.230
Okay so that's this interval.
0:04:14.230,0:04:20.209
It is c -- delta to c + delta except you
don't really care about the point c itself,
0:04:20.209,0:04:26.490
(but that's a little subtlety we don't
have to bother about), so the skeptic is choosing
0:04:26.490,0:04:29.780
the interval like this.
The prover is choosing the interval like this.
0:04:29.780,0:04:33.340
How is the skeptic choosing the interval? By just
specifying the value of epsilon.
0:04:33.340,0:04:34.880
How is the prover choosing [the interval around c]?
0:04:34.880,0:04:45.880
By just specifying a value of delta. Okay.
Now what does the skeptic now do? [ANSWER!]
0:04:46.500,0:04:52.979
Rui: Skeptic will check.
0:04:53.079,0:05:00.079
Vipul: There is something more to choose (right?)
before checking.
0:05:02.710,0:05:06.599
What does the definition say? For every epsilon
> 0 there exists a delta greater than zero
0:05:06.599,0:05:07.259
such that ... [COMPLETE!]
0:05:07.259,0:05:08.580
Rui: For every.
0:05:08.580,0:05:13.220
Vipul: For every x such that something. The
skeptic can now pick x.
0:05:13.220,0:05:17.000
Rui: That's what I meant by checking.
0:05:17.000,0:05:21.940
Vipul: The skeptic could still, like, pick a
value to challenge the prover.
0:05:21.940,0:05:28.940
The skeptic chooses x but what x can the skeptic
choose?
0:05:29.169,0:05:31.810
Rui: Within the...
0:05:31.810,0:05:36.590
Vipul: This interval which the prover has
specified.
0:05:36.590,0:05:43.590
The skeptic is constrained to choose x within
the interval.
0:05:44.250,0:05:49.639
That's the same as c -- delta ... Is this
all coming?
0:05:49.639,0:05:50.330
Rui: Yes.
0:05:50.330,0:05:57.330
Vipul: c -- delta, c union c to c + delta.
0:05:59.110,0:06:15.110
The way it's written is for every x in this
interval.
0:06:16.849,0:06:21.349
Lot of people write this in a slightly different
way.
0:06:21.349,0:06:28.349
They write it as ...
0:06:28.400,0:06:31.720
(You should see the definition video before
this.)
0:06:31.720,0:06:37.729
(I'm sort of assuming that you have seen the
definition -- this part [of the screen] so you can map it)
0:06:37.729,0:06:40.000
so a lot of people write it like this.
0:06:40.000,0:06:45.190
It is just saying x is within delta distance
of c but it's not equal to c itself.
0:06:45.190,0:06:50.949
Now it's time for the judge to come in and
decide who has won.
0:06:50.949,0:06:55.930
How does the judge decide? [ANSWER!]
0:06:55.930,0:07:01.360
Rui: For the x that the skeptic chooses and
see the corresponding y.
0:07:01.360,0:07:03.289
Vipul: The f(x) value.
0:07:03.289,0:07:10.289
Rui: If the f(x) value is within the horizontal strip then the prover wins.
0:07:12.509,0:07:30.000
Vipul: If |f(x) -- L| < epsilon which is the same
as saying f(x) is in what interval? [ANSWER!]
0:07:30.000,0:07:41.620
L- epsilon to L + epsilon then the prover
wins. Otherwise? [ANSWER!]
0:07:42.120,0:07:46.120
Rui: The skeptic wins.
0:07:46.120,0:07:53.120
[But] the skeptic can choose a really dumb [stupid] x.
0:07:54.039,0:07:57.610
Vipul: That's actually the next question
I want to ask you.
0:07:57.610,0:08:01.240
What does it actually mean to say that this
statement is true?
0:08:01.240,0:08:04.770
Is it just enough that the prover wins? That's
not enough.
0:08:04.770,0:08:07.909
What do you want to say to say that this statement
is true?
0:08:07.909,0:08:11.210
Rui: For every x in the interval.
0:08:11.210,0:08:16.289
Vipul: For every x but not only for every
x you should also say for every epsilon.
0:08:16.289,0:08:22.139
All the moves that the skeptic makes, the prover
should have a strategy, which works for all of them.
0:08:22.139,0:08:25.710
So, this statement is true [if] ...
0:08:25.710,0:08:29.800
This is true if the prover has what for the
game? [ANSWER!]
0:08:30.539,0:08:35.050
Rui: Winning strategy.
Vipul: Winning what?
Rui: Strategy.
0:08:35.050,0:08:38.669
Vipul: Yeah. True if the prover has a winning strategy.
0:08:38.669,0:08:44.910
It is not just enough to say that the prover
won the game some day but the prover should
0:08:44.910,0:08:50.220
be able to win the game regardless of how
smart the skeptic is or regardless of how
0:08:50.220,0:08:53.960
experienced the skeptic is or regardless of
how the skeptic plays.
0:08:53.960,0:09:00.960
That's why all the moves of the skeptic
are prefaced with a "for every." Right?
0:09:02.230,0:09:07.560
Whereas all the moves of the prover are prefaced,
(well there is only one move really of the
0:09:07.560,0:09:11.180
prover) are prefaced with "there exists"
because the prover controls his own choices.
0:09:11.180,0:09:15.360
When it is the prover's turn it's enough
to say "there exists" but since the prover doesn't
0:09:15.360,0:09:21.590
control what the skeptic does all the skeptic
moves are prefaced with "for every."
0:09:21.590,0:09:26.150
By the way, there is a mathematical notation
for these things.
0:09:26.150,0:09:31.730
There are mathematical symbols for these,
which I'm not introducing in this video,
0:09:31.730,0:09:37.920
but if you have seen them and got confused
then you can look at the future video where
0:09:37.920,0:09:40.500
I explain the mathematical symbols.
Negation of limit statement and non-existence of limit
We now consider the explicit description of the definition for the case that the skeptic has a winning strategy for the limit game for  , i.e., for the limit statement being false.
, i.e., for the limit statement being false.
In words, the definition is:
There exists  such that for every
such that for every  , there exists
, there exists  satisfying
satisfying  and
and  .
.
Let's review the definition in conjunction with the game along with a deeper semantic understanding of the steps:
| Step no. |
Clause of definition for original limit statement (i.e., prover has a winning strategy) |
Clause of definition for skeptic having a winning strategy |
Who moves? |
What is chosen? |
Constraints on the choice |
Comment
|
| 1 |
For every  |
There exists  such that such that |
Skeptic |
 |
Must be positive |
Whether we use "for every" or "there exists" depends on who we're rooting for.
|
| 2 |
there exists  such that such that |
for every  , , |
Prover |
 |
Must be positive |
Whether we use "for every" or "there exists" depends on who we're rooting for.
|
| 3 |
for all  satisfying satisfying  , , |
there exists  satisfying satisfying  and and |
Skeptic |
 |
Must be within the interval  |
Whether we use "for every" or "there exists" depends on who we're rooting for.
|
| 4 |
we have  |
 . . |
Neither; it's time for the judge to decide |
-- |
If  , the prover wins. Else, the skeptic wins. , the prover wins. Else, the skeptic wins. |
The conditions are negatives of one another.
|
{{#widget:YouTube|id=N0U8Y11nlPk}}
Full timed transcript: [SHOW MORE]
0:01:26.720,0:01:33.720
Ok, so in this talk, we are going to give the definition
of what it means to say that this statement,
0:01:34.250,0:01:37.940
the one up here, is false.
0:01:37.940,0:01:41.300
So far we've looked at what it means for this
statement to be true.
0:01:41.300,0:01:44.960
Now we are going to look at what it means
for the statement to be false.
0:01:44.960,0:01:48.340
Basically, you just use the same definition,
but you would change a little bit of what
0:01:48.340,0:01:49.490
it looks like.
0:01:49.490,0:01:54.130
Let me first remind you of the limit game
because that is a very nice way of thinking
0:01:54.130,0:01:57.380
about what it means to be true and false.
0:01:57.380,0:01:58.860
What does the limit game say?
0:01:58.860,0:02:01.680
It is a game between two players, a prover
and a skeptic.
0:02:01.680,0:02:04.680
What is the goal of the prover? [ANSWER!]
0:02:04.680,0:02:06.310
Rui: To show he is right.
0:02:06.310,0:02:07.930
Vipul: To show that this is true.
0:02:07.930,0:02:08.489
Rui: True.
0:02:08.489,0:02:12.830
Vipul: The skeptic is trying to show that
this is false, or at least trying to come
0:02:12.830,0:02:16.730
up with the strongest evidence to suggest
that this is false.
0:02:16.730,0:02:18.090
How does the game proceed?
0:02:18.090,0:02:23.349
The skeptic begins by choosing an epsilon
greater than zero.
0:02:23.349,0:02:25.200
What is the skeptic effectively trying to
pick?
0:02:25.200,0:02:30.769
The skeptic is effectively trying to pick
this neighborhood of L and trying to challenge
0:02:30.769,0:02:36.579
the prover to trap the function value for
x within that neighborhood.
0:02:36.579,0:02:40.719
What's that neighborhood the skeptic is
secretly picking? [ANSWER!]
0:02:40.719,0:02:43.909
Rui: L -- epsilon [to L + epsilon]
0:02:43.909,0:02:50.909
Vipul: Ok, the prover chooses a delta greater
than zero so the prover is now basically trying
0:02:53.040,0:03:00.040
to pick a neighborhood of c, the point near the
domain points, and
0:03:02.650,0:03:09.650
then the skeptic will then pick a value x, which is within the interval delta distance
of c except the point c itself.
0:03:10.120,0:03:16.200
That's either delta interval on the left
or delta interval on the right of c.
0:03:16.200,0:03:20.569
Then the judge comes along and computes this
value, absolute value f(x) minus...Are we,
0:03:20.569,0:03:21.739
is this in the picture?
0:03:21.739,0:03:22.700
Rui: Yes.
0:03:22.700,0:03:27.329
Vipul: If it is less than epsilon then the
prover would have won, but now we want to
0:03:27.329,0:03:34.329
see if the skeptic wins if it is greater or
equal to epsilon, that means f(x) is not in
0:03:35.569,0:03:36.129
the epsilon...
0:03:36.129,0:03:37.249
Rui: Neighborhood.
0:03:37.249,0:03:42.459
Vipul: This video assumes you have already
seen the previous videos where we give these
0:03:42.459,0:03:48.689
definitions and so I'm sort of reviewing it
quickly, but not explaining it in full detail.
0:03:48.689,0:03:54.069
So, the skeptic wins if f(x) is outside this
interval, that means the prover failed to
0:03:54.069,0:03:58.069
rise to the skeptic's challenge of trapping
the function.
0:03:58.069,0:04:05.069
Let's now try to work out concretely what
the definition would read.
0:04:06.590,0:04:10.439
The skeptic is the one in control because
you want to figure out whether the skeptic
0:04:10.439,0:04:12.639
has a winning strategy.
0:04:12.639,0:04:17.690
Ok, so let me just say this clearly, this
is just saying when does the skeptic win?
0:04:17.690,0:04:21.090
Now in order to say this limit statement is
false, we need something stronger. What do
0:04:21.090,0:04:25.360
we need to say this is false? [ANSWER!]
0:04:25.360,0:04:26.450
The skeptic should have...
0:04:26.450,0:04:28.820
Rui: Should have a winning strategy.
0:04:28.820,0:04:30.410
Vipul: A winning strategy.
0:04:30.410,0:04:34.229
The skeptic should have a strategy so that
whatever the prover does, the skeptic has
0:04:34.229,0:04:36.139
some way of winning.
0:04:36.139,0:04:41.229
What should this read...if you actually translate
it to the definition?
0:04:41.229,0:04:44.169
Rui: There exists an...
0:04:44.169,0:04:46.000
Vipul: There exists epsilon
0:04:46.000,0:04:51.000
Rui: ...an epsilon greater than zero.
0:04:58.000,0:05:00.000
Vipul: Okay. Such that...
0:05:00.280,0:05:07.210
Rui: For every delta greater than zero.
0:05:07.210,0:05:10.870
Vipul: So the skeptic, when it's the skeptic's
move the skeptic says "there exists."
0:05:10.870,0:05:14.310
If anything works, the skeptic can pick that,
but when it's the provers move, the skeptic
0:05:14.310,0:05:15.699
has no control.
0:05:15.699,0:05:30.699
This should read, for every delta greater
than zero...What will the next part read?
0:05:31.770,0:05:33.930
Rui: There exists an x.
0:05:33.930,0:05:40.930
Vipul: Exists x in this interval.
0:05:44.289,0:05:45.340
Rui: Yeah.
0:05:45.340,0:05:50.159
Vipul: Which you often see it written in a
slightly different form.
0:05:50.159,0:05:57.159
Maybe, I don't have space here, so here
it is also written as "0 ...", are we down here?
0:05:59.960,0:06:01.560
Rui: Yes.
0:06:01.560,0:06:04.470
Vipul: This is the form it's usually written in
concise definitions.
0:06:04.470,0:06:20.710
We have this...So the definition, maybe it's not
clear, but the definition would read like that.
0:06:20.710,0:06:25.419
So there exists Epsilon greater than zero such
that for every delta greater than zero there
0:06:25.419,0:06:30.879
exists x, in here, which you could also write
like this, such that, I guess I should put
0:06:30.879,0:06:35.310
the "such that." [writes it down]
0:06:35.310,0:06:39.849
Such that. absolute value of f(x) -- L is greater
than or equal to epsilon
0:06:39.849,0:06:44.680
Let me just compare it with the usual definition
for the limit to exist.
0:06:44.680,0:06:47.750
The colors are in a reverse chrome.
0:06:47.750,0:06:52.860
That's fine. For every epsilon greater than
zero became there exists epsilon greater than
0:06:52.860,0:06:55.879
zero because the player who is in control
has changed.
0:06:55.879,0:06:59.789
There exists delta greater than zero became
for every delta greater than zero, for all
0:06:59.789,0:07:05.139
x with this became their exists x satisfying
this condition.
0:07:05.139,0:07:07.629
What happened to the last clause?
0:07:07.629,0:07:12.099
The less than Epsilon begin greater than or
equal to.
0:07:12.099,0:07:17.069
The last clause just got reversed in meaning,
all the others, we just changed the quantifier
0:07:17.069,0:07:22.389
from "for all" to "there exists" and from "there
exists" to "for all" and that is just because
0:07:22.389,0:07:25.770
we changed who is winning.
0:07:25.770,0:07:30.439
If you have seen some logic, if you ever see
logic, then there are some general rules of
0:07:30.439,0:07:33.650
logic as to how to convert a statement to
its opposite statement.
0:07:33.650,0:07:38.610
This is a general rule that "for all" becomes
"there exists" and "there exists" becomes "for all."
Non-existence of limit
The statement  does not exist could mean one of two things:
does not exist could mean one of two things:
 is not defined around
is not defined around  , i.e., there is no
, i.e., there is no  for which
for which  is defined on
is defined on  . In this case, it does not even make sense to try taking a limit.
. In this case, it does not even make sense to try taking a limit. is defined around
is defined around  , except possibly at
, except possibly at  , i.e., there is
, i.e., there is  for which
for which  is defined on
is defined on  . So, it does make sense to try taking a limit. However, the limit still does not exist.
. So, it does make sense to try taking a limit. However, the limit still does not exist.
The formulation of the latter case is as follows:
For every  , there exists
, there exists  such that for every
such that for every  , there exists
, there exists  satisfying
satisfying  and such that
and such that  .
.
We can think of this in terms of a slight modification of the limit game, where, in our modification, there is an extra initial move by the prover to propose a value  for the limit. The limit does not exist if the skeptic has a winning strategy for this modified game.
for the limit. The limit does not exist if the skeptic has a winning strategy for this modified game.
An example of a function that does not have a limit at a specific point is the sine of reciprocal function. Explicitly, the limit:

does not exist. The skeptic's winning strategy is as follows: regardless of the  chosen by the prover, pick a fixed
chosen by the prover, pick a fixed  (independent of
(independent of  , so
, so  can be decided in advance of the game -- note that the skeptic could even pick
can be decided in advance of the game -- note that the skeptic could even pick  and the strategy would still work). After the prover has chosen a value
and the strategy would still work). After the prover has chosen a value  , find a value
, find a value  such that the
such that the  function value lies outside
function value lies outside  . This is possible because the interval
. This is possible because the interval  has width
has width  , hence cannot cover the entire interval
, hence cannot cover the entire interval ![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01) , which has width 2. However, the range of the
, which has width 2. However, the range of the  function on
function on  is all of
is all of ![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01) .
.
Crucially, the inability of the prover to trap the function value close to any point as  is the reason the limit fails to exist.
is the reason the limit fails to exist.
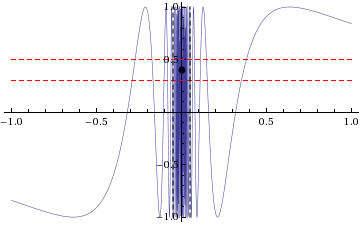
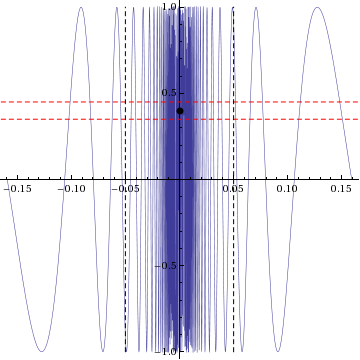
{{#widget:YouTube|id=JoVuC4pksWs}}
Full timed transcript: [SHOW MORE]
0:00:31.170,0:00:38.170
Vipul: Ok, so this talk is going to be about
why under certain circumstances limits don't exist
0:00:39.800,0:00:46.800
We are going to take this example of a function
which is defined like this: sin of one over x
0:00:47.699,0:00:51.360
Obviously, that definition doesn't work
when x equals zero.
0:00:51.360,0:00:57.260
So this is a function defined only for all non-zero
reals.
0:00:57.260,0:01:01.050
The goal is to figure out what the limit as
x approaches 0 of f(x) is.
0:01:01.050,0:01:06.630
Here is a graph of the function. This is a
y axis, and x axis.
0:01:06.630,0:01:08.490
The function looks like this.
0:01:08.490,0:01:10.680
It is oscillatory.
0:01:10.680,0:01:16.270
As you approach zero it oscillates more, faster
and faster.
0:01:16.270,0:01:19.070
What are the upper and lower limits of oscillation?
0:01:19.070,0:01:25.580
Actually all these things should be the same
height.
0:01:25.580,0:01:29.760
My drawing wasn't good, but, it should all
be the same height, above and below.
0:01:29.760,0:01:31.290
What are these upper and lower limits? [ANSWER!]
0:01:31.290,0:01:32.790
Rui: 1 and -1.
0:01:32.790,0:01:39.790
Vipul: So the lower limit is negative one
and the upper limit is one. Ok, good.
0:01:39.829,0:01:46.829
So what does it mean, what is the limit at
zero for this function? [ANSWER!]
0:01:46.850,0:01:53.850
This is where...you need to really think, so
I might say ok the limit is, looks like it's zero.
0:01:58.259,0:01:58.509
0:01:58.469,0:02:04.749
At zero, you say that looks neat, that looks
right because you see when the x value approaches,
0:02:04.749,0:02:09.190
comes close to zero, the f(x) value also comes
close to zero.
0:02:09.190,0:02:12.700
It keeps oscillating between -1and 1,
and it keeps coming.
0:02:12.700,0:02:19.700
I draw a very small ball around zero, like
that.
0:02:19.780,0:02:22.700
The function is going to keep entering this
ball.
0:02:22.700,0:02:27.060
A ball or a square one or whatever.
0:02:27.060,0:02:34.060
A very small neighborhood of this origin point
here in this two-dimensional picture.
0:02:35.230,0:02:40.459
The function graph is going to enter that
repeatedly.
0:02:40.459,0:02:42.010
Do you think the limit is zero? [ANSWER!]
0:02:42.010,0:02:42.830
Rui: No.
0:02:42.830,0:02:46.860
Vipul: No? Why not? Isn't it coming really
close to zero?
0:02:46.860,0:02:47.430
Rui: Sometimes.
0:02:47.430,0:02:49.140
Vipul: What do you mean "sometimes?"
0:02:49.140,0:02:56.140
Rui: It means sometimes it is real close to
zero and then it flies away.
0:02:56.870,0:03:03.870
Vipul: Ok, "flies away." [Hmm] So what's
your objection? What is not happening?
0:03:04.019,0:03:06.010
Rui: We can not trap.
0:03:06.010,0:03:07.239
Vipul: We cannot trap...
0:03:07.239,0:03:11.909
Rui: ...trap it in a neighborhood of zero.
0:03:11.909,0:03:18.480
Vipul: Function not trapped.
0:03:18.480,0:03:20.110
What should the limit be if it is not zero?
0:03:20.110,0:03:24.849
Should it be half, two-thirds, what should
the limit be? [ANSWER!]
0:03:24.849,0:03:31.849
(I'll explain this later), what do you think
the limit should be?
0:03:34.659,0:03:36.730
Rui: It doesn't have a limit.
0:03:36.730,0:03:38.299
Vipul: It doesn't have a limit.
0:03:38.299,0:03:39.790
Ok, so what does that mean?
0:03:39.790,0:03:45.290
Whatever limit you claim the function has
you are wrong...If you claim the function had
0:03:45.290,0:03:49.170
any numerical limit, if you claim if it is half you
are wrong.
0:03:49.170,0:03:50.640
If you claim minus half you are wrong.
0:03:50.640,0:03:52.720
If you claim the limit is 50, you are wrong.
0:03:52.720,0:03:54.959
Whatever claim you make about the limit,
you are wrong.
0:03:54.959,0:04:00.780
So let's try to think of this in terms of the
game between a prover and a skeptic.
0:04:00.780,0:04:02.730
(You should go and review that video
0:04:02.730,0:04:09.730
or read the corresponding material to understand
what I am going to say.)
0:04:09.829,0:04:13.969
It's good if you have also seen the video
on the definition of limit statement being
0:04:13.969,0:04:17.709
false, which builds on that.
0:04:17.709,0:04:21.620
What I am now asking you, what does it mean
to say the limit does not exist?
0:04:21.620,0:04:23.980
As x approaches c [limit] of f(x) does not exist.
0:04:23.980,0:04:27.810
Here c is zero, but that is not relevant...
that is not necessary for the definition.
0:04:27.810,0:04:32.910
Well it is the usual way we say that the
limit statement is false except we need to
0:04:32.910,0:04:37.170
add one step in the beginning, which is for
every L in R [the reals].
0:04:37.170,0:04:42.460
It says that for every L in R [the reals] the statement
limit x approaches c, f(x) equals L, is false.
0:04:42.460,0:04:43.900
So how does it read?
0:04:43.900,0:04:48.220
It says, for every L in R [the reals] there exists epsilon
greater than zero such that for every delta
0:04:48.220,0:04:55.030
greater than zero there exists x, within the
delta neighborhood of c such that f(x) is
0:04:55.030,0:04:58.590
not in the epsilon neighborhood of L.
0:04:58.590,0:05:05.590
How would you interpret this in terms of a
game between a prover and a skeptic?[ANSWER, THINKING ALONG!]
0:05:06.470,0:05:11.570
Rui: For every limit the prover proposes...
0:05:11.570,0:05:16.420
Vipul: This is not quite the same as the limit
game which you may have seen in a previous
0:05:16.420,0:05:21.170
video which was assuming that the limit was
already given as a part of the game.
0:05:21.170,0:05:28.170
This is sort of a somewhat more general game or
a more meta game where part of the game
0:05:28.420,0:05:31.950
is also the prover trying to specify what
the limit should be.
0:05:31.950,0:05:37.100
The first step the prover plays, the prover
is in black, skeptic is in red.
0:05:37.100,0:05:43.290
The first step the prover plays, proposes
a value of the limit. Then?
0:05:43.290,0:05:47.280
Rui: The skeptic chooses an epsilon.
0:05:47.280,0:05:50.020
Vipul: What's the goal of the skeptic in choosing
the epsilon?
0:05:50.020,0:05:56.740
The goal of the skeptic is.. so let's say
the prover chose a limit value L here, that's
0:05:56.740,0:05:58.470
numerical value L here.
0:05:58.470,0:06:00.050
The skeptic picks epsilon.
0:06:00.050,0:06:06.650
The skeptic will pick epsilon, which means
the skeptic is picking this band from L minus
0:06:06.650,0:06:12.400
epsilon to L plus epsilon.
0:06:12.400,0:06:14.270
Now what does the prover try to do?
0:06:14.270,0:06:19.000
The prover tries to pick a delta. What is
the prover trying to do?
0:06:19.000,0:06:24.490
Find a neighborhood of c, such that the
function in that neighborhood of c the function
0:06:24.490,0:06:28.370
is trapped within epsilon of L.
0:06:28.370,0:06:32.740
So in our case, c is zero in this example,
so the prover will be trying to pick a neighborhood
0:06:32.740,0:06:39.740
of zero, is something like... zero plus delta
on the right and zero minus delta on the left.
0:06:44.620,0:06:45.750
What's the goal of the prover?
0:06:45.750,0:06:50.840
To say that whenever x is in this interval,
for all x,
0:06:50.840,0:06:53.500
The prover is trying to say that all for x
in here, the function [difference from L] is less than epsilon.
0:06:53.500,0:06:56.170
The skeptic who is trying to disprove that.
0:06:56.170,0:06:59.060
What does the skeptic need to do?
0:06:59.060,0:07:03.900
Rui: Every time the prover finds an x.
0:07:03.900,0:07:07.540
Vipul: Well the prover finds, picks the delta,
what does the skeptic try to do?
0:07:07.540,0:07:08.480
Rui: Just pick an x.
0:07:08.480,0:07:10.550
Vipul: Picks an x such that the function...
0:07:10.550,0:07:12.140
Rui: Is out of the...
0:07:12.140,0:07:13.960
Vipul: Is outside that thing.
0:07:13.960,0:07:24.960
Let me make this part a little bit more...so
here you have... the same colors.
0:07:25.150,0:07:41.150
This is
the axis...The skeptic...The prover has picked
this point and the skeptic has picked epsilon.
0:07:41.780,0:07:46.670
So this is L plus epsilon, L minus epsilon.
0:07:46.670,0:07:50.460
The prover is now, it so happens that c is
zero here.
0:07:50.460,0:07:56.690
So that everything is happening near the y
axis.
0:07:56.690,0:08:03.690
Now, the prover wants to pick a delta, the
prover wants to pick, like this, should be
0:08:07.320,0:08:07.910
the same.
0:08:07.910,0:08:14.910
So this is c plus delta which c is zero, so
zero plus delta and zero minus delta.
0:08:17.810,0:08:21.960
Now, under what conditions...What happens
next?
0:08:21.960,0:08:28.240
The prover is implicitly trying to claim that
the function, when the x value is close here,
0:08:28.240,0:08:30.520
the function value is trapped here.
0:08:30.520,0:08:35.089
What the skeptic wants to show is that, that's
not true.
0:08:35.089,0:08:39.830
If it isn't true, in order to do that, the
skeptic should pick a value of x.
0:08:39.830,0:08:46.830
So the skeptic needs to pick a value of x
somewhere in this interval such that at that
0:08:48.110,0:08:55.110
value of f(x)...let me just make the x axis...so
the skeptic wants to pick a value of x, maybe
0:08:59.209,0:09:06.209
its somewhere here, such that when you evaluate
the function at x it lies outside.
0:09:07.269,0:09:11.720
If when you evaluate the function at x, and it lies
outside this strip then the skeptic wins and
0:09:11.720,0:09:16.290
if the value of the function of x is inside
the strip then the prover wins.
0:09:16.290,0:09:23.290
Now looking back at this function, the question
is, can the prover pick an L such that regardless,
0:09:25.209,0:09:31.779
so can the prover pick a value of L such that...Is
this whole thing coming?
0:09:31.779,0:09:37.860
Such that regardless of the epsilon that the
skeptic picks, there exists a delta such that
0:09:37.860,0:09:44.439
for all x the function is trapped? Or is it
instead true that the skeptic will win? (i.e.) Is
0:09:44.439,0:09:50.579
it true that whatever L the prover picks there
exists an epsilon, since the skeptic picks
0:09:50.579,0:09:57.360
an epsilon, such that whatever delta the prover
picks the function in not in fact, trapped
0:09:57.360,0:10:00.399
here. What do you think looking at the picture
here?
0:10:00.399,0:10:05.329
Can you trap the function in a rectangle
like this? [ANSWER!]
0:10:05.329,0:10:06.100
Rui: No.
0:10:06.100,0:10:09.930
Vipul: Well, not if it is a very small rectangle.
0:10:09.930,0:10:16.930
What should the skeptic's strategy be?
0:10:17.060,0:10:23.930
The claim is that the limit does not exist,
that is the claim.
0:10:23.930,0:10:25.990
The claim is that this limit doesn't exist.
0:10:25.990,0:10:29.750
What is the skeptic's strategy?
0:10:29.750,0:10:31.990
What do you mean by skeptic strategy?
0:10:31.990,0:10:37.370
Well, the skeptic should have some strategy
that works, so the skeptic should pick an
0:10:37.370,0:10:43.290
epsilon that is smart and then the skeptic
should pick an x that works.
0:10:43.290,0:10:50.209
What epsilon should the skeptic pick? Suppose
the skeptic picks epsilon as 50 million,
0:10:50.209,0:10:52.050
is that a winning strategy?
0:10:52.050,0:10:52.790
Rui: No.
0:10:52.790,0:10:53.899
Vipul: Why not?
0:10:53.899,0:10:58.300
Rui: He should pick something between -1 and
1, right?
0:10:58.300,0:11:01.920
Vipul: Well epsilon is a positive number so
what do you mean?
0:11:01.920,0:11:04.600
Rui: Oh, anything between one, smaller.
0:11:04.600,0:11:05.230
Vipul: Smaller than...
0:11:05.230,0:11:08.999
Rui: Less than one. Epsilon.
0:11:08.999,0:11:12.470
Vipul: Less than one. Why will that work?
0:11:12.470,0:11:19.470
Rui: Because even if it is less than one then
anything, no matter what kind of delta...
0:11:20.930,0:11:27.930
Vipul: Whatever L the prover picked...What
is the width of this interval? The distance
0:11:28.209,0:11:29.589
from the top and the bottom is?
0:11:29.589,0:11:30.279
Rui: 2
0:11:30.279,0:11:30.980
Vipul: [2 times] epsilon.
0:11:30.980,0:11:31.680
Rui: [2 times] epsilon.
0:11:31.680,0:11:38.680
Vipul: 2 epsilon. If epsilon
is less than one, the skeptic's strategy is
pick epsilon less than one any epsilon.
0:11:43.089,0:11:50.089
The skeptic can fix epsilon in the beginning, maybe pick
epsilon as 0.1 or something, but any epsilon
0:11:50.610,0:11:52.019
less than one will do.
0:11:52.019,0:11:59.019
In fact epsilon equal to one will do. Let
us play safe and pick epsilon as 0.1.
0:11:59.810,0:12:00.999
Why does it work?
0:12:00.999,0:12:06.600
Because this 2 epsilon cannot include both
one and minus one.
0:12:06.600,0:12:12.649
It cannot cover this entire thing because
this has width two, from one to minus one.
0:12:12.649,0:12:17.589
If the skeptic picks an epsilon less than
one, regardless of the L the prover has tried,
0:12:17.589,0:12:23.079
the strip is not wide enough to include everything
from minus one to one.
0:12:23.079,0:12:27.990
Regardless of what Delta the prover picks,
we know that however small an interval we
0:12:27.990,0:12:32.180
pick around zero, the function is going to
take all values from negative one to one in
0:12:32.180,0:12:35.759
that small interval.
0:12:35.759,0:12:40.819
Now the skeptic will be able to find an x
such that the function value lies outside
0:12:40.819,0:12:42.290
the interval.
0:12:42.290,0:12:45.579
The skeptic should...the key idea is that
the skeptic pick epsilon small enough, in
0:12:45.579,0:12:50.360
this case the skeptic's choice of epsilon
doesn't depend on what L the prover chose.
0:12:50.360,0:12:51.269
It need not.
0:12:51.269,0:12:52.889
The strategy doesn't.
0:12:52.889,0:12:59.889
Then after the prover has picked a delta,
picked an x such that the function lies outside.
0:13:01.249,0:13:07.410
Regardless of the L the prover picks,
that L doesn't work as a limit because
0:13:07.410,0:13:10.550
the skeptic wins and so the limit doesn't
exist.
Strategic aspects
The strategy of small
In the game formulation of the limit, the following loose statements are true:
- "Smaller is smarter" for the skeptic, i.e., the smaller the choice of
 , the better the outlook is for the skeptic to win.
, the better the outlook is for the skeptic to win.
- "Smaller is smarter" for the prover, i.e., the smaller the choice of
 , the better the outlook is for the prover to win.
, the better the outlook is for the prover to win.
In other words, each side benefits by making the crucial move of that side as small as possible. However, there does not exist any single arbitrarily small number -- this is related to the observation in the motivation section that there is no such thing as a single arbitrarily close number. Thus, saying "choose as small a value as possible" is not a coherent strategy. What we can say is the following:
- If a value of
 works for a given value of
works for a given value of  , the same value of
, the same value of  also works for larger choices of
also works for larger choices of  .
.
- If a value of
 works for a given value of
works for a given value of  , smaller values of
, smaller values of  also work for the same choice of
also work for the same choice of  .
.
Prover's strategy revisited
The prover, in choosing a winning strategy, must specify a rule that can determine a value of  that works in terms of the value of
that works in terms of the value of  specified by the skeptic. In other words, the prover must have a way of specifying
specified by the skeptic. In other words, the prover must have a way of specifying  as a function of
as a function of  .
.
The skeptic also chooses  in the next move. However, the prover has no way of knowing the value of
in the next move. However, the prover has no way of knowing the value of  that the skeptic plans to pick. Thus, in order for the prover to have a winning strategy, the prover's choice of
that the skeptic plans to pick. Thus, in order for the prover to have a winning strategy, the prover's choice of  should be such that no matter what
should be such that no matter what  the skeptic picks, the prover wins.
the skeptic picks, the prover wins.
Skeptic's strategy revisited
The skeptic, in choosing a winning strategy, must specify the value of  and then specify how to pick a value of
and then specify how to pick a value of  that works. When picking the value of
that works. When picking the value of  , the skeptic does not know what
, the skeptic does not know what  the prover will pick. Thus, the skeptic's choice of
the prover will pick. Thus, the skeptic's choice of  cannot be dependent on the prover's subsequent choice of
cannot be dependent on the prover's subsequent choice of  .
.
However, when picking the value of  , the skeptic is aware of (and constrained by) the prover's choice of
, the skeptic is aware of (and constrained by) the prover's choice of  .
.
Misconceptions
Most misconceptions associated with the formal  definition of limit have to do with the ordering of the moves in the game, who's in charge of what move, and what information each person has at the time of making the move. We describe some common misconceptions below.
definition of limit have to do with the ordering of the moves in the game, who's in charge of what move, and what information each person has at the time of making the move. We describe some common misconceptions below.
{{#widget:YouTube|id=F0r_offAc5M}}
Full timed transcript: [SHOW MORE]
0:00:15.500,0:00:19.140
Vipul: Okay. This talk is going to be about
certain misconceptions
0:00:19.140,0:00:22.440
that people have regarding limits and these
are misconceptions that
0:00:22.440,0:00:25.840
people generally acquire after...
0:00:25.840,0:00:29.180
These are not the misconceptions that
people have before studying limits,
0:00:29.180,0:00:32.730
these are misconceptions you might have after
studying limits,
0:00:32.730,0:00:35.059
after studying the epsilon delta definition.
0:00:35.059,0:00:38.550
I'm going to describe these misconceptions
in terms of the limit game,
0:00:38.550,0:00:41.900
the prover skeptic game of the limit. Though
the misconceptions
0:00:41.900,0:00:45.850
themselves don't depend on
the understanding of the
0:00:45.850,0:00:49.059
game but to understand exactly what's
happening, it's better to think
0:00:49.059,0:00:51.010
of it in terms of the game.
0:00:51.010,0:00:55.370
First recall the definition. So limit as x
approaches c of f(x) is a
0:00:55.370,0:01:01.629
number L; so c and L are both numbers, real
numbers. f is a function,
0:01:01.629,0:01:06.380
x is approaching c. And we said this is true
if the following -- for
0:01:06.380,0:01:10.180
every epsilon greater than zero, there exists
a delta greater than
0:01:10.180,0:01:14.800
zero such that for all x which are within delta
distance of c, f(x) is
0:01:14.800,0:01:17.590
within epsilon distance of L. Okay?
0:01:17.590,0:01:24.590
Now, how do we describe this in terms for
limit game?
0:01:26.530,0:01:33.530
KM: So, skeptic starts off with the first
part of the definition.
0:01:34.990,0:01:38.189
Vipul: By picking the epsilon? Okay, that's
the thing written in
0:01:38.189,0:01:42.939
black. What's the skeptic trying to do? What's the
goal of the skeptic?
0:01:42.939,0:01:49.100
KM: To try and pick an epsilon that would
not work.
0:01:49.100,0:01:53.450
Vipul: So the goal of the skeptic is to try
to show that the statement is false.
0:01:53.450,0:01:54.100
KM: Yeah.
0:01:54.100,0:01:57.790
Vipul: Right? In this case the skeptic should
try to start by choosing
0:01:57.790,0:02:02.220
an epsilon that is really [small] -- the goal of
the skeptic is to pick an
0:02:02.220,0:02:04.500
epsilon that's really small, what is the
skeptic trying to challenge
0:02:04.500,0:02:07.920
the prover into doing by picking the epsilon?
The skeptic is trying to
0:02:07.920,0:02:11.959
challenge the prover into trapping the function
close to L when x is
0:02:11.959,0:02:17.040
close to c. And the way the skeptic specifies
what is meant by "close to L" is
0:02:17.040,0:02:19.860
by the choice of epsilon. Okay?
0:02:19.860,0:02:24.900
When picking epsilon the skeptic is
effectively picking this interval, L -
0:02:24.900,0:02:30.700
epsilon, L + epsilon). Okay? And basically
that's what the skeptic is
0:02:30.700,0:02:33.680
doing. The prover is then picking a delta.
What is the goal of the
0:02:33.680,0:02:36.239
prover in picking the delta? The prover is
saying, "Here's how I can
0:02:36.239,0:02:40.099
trap the function within that interval. I'm
going to pick a delta and
0:02:40.099,0:02:43.520
my claim is that if the x value within delta distance of c, except the
0:02:43.520,0:02:47.000
point c itself, so my claim is for any x value
there the function is
0:02:47.000,0:02:48.260
trapped in here."
0:02:48.260,0:02:52.819
So, the prover picks the delta and then the
skeptic tries to
0:02:52.819,0:02:56.709
test the prover's claim by picking an x
0:02:56.709,0:02:59.670
which is within the interval specified by
the prover and then they
0:02:59.670,0:03:03.379
both check whether f(x) is within epsilon
distance [of L]. If it is
0:03:03.379,0:03:07.940
then the prover wins and if it is not, if
this [|f(x) - L|]is not less
0:03:07.940,0:03:09.989
than epsilon then the skeptic wins. Okay?
0:03:09.989,0:03:13.659
So, the skeptic is picking the neighborhood
of the target point which
0:03:13.659,0:03:17.030
in this case is just the open interval of
radius epsilon, the prover
0:03:17.030,0:03:21.940
is picking the delta which is effectively the
neighborhood of the domain
0:03:21.940,0:03:25.760
point except the point c as I've said open
interval (c - delta, c +
0:03:25.760,0:03:30.870
delta) excluding c and then the skeptic picks
an x in the neighborhood
0:03:30.870,0:03:35.700
specified by prover and if the function value
is within the interval
0:03:35.700,0:03:38.830
specified by the skeptic then the prover wins.
0:03:38.830,0:03:41.989
Now, what does it mean to say the statement
is true in terms of the
0:03:41.989,0:03:43.080
game?
0:03:43.080,0:03:50.080
KM: So, it means that the prover is always
going to win the game.
0:03:51.849,0:03:55.629
Vipul: Well, sort of. I mean the prover may
play it stupidly. The
0:03:55.629,0:04:00.750
prover can win the game if the prover plays
well. So, the prover has a
0:04:00.750,0:04:03.230
winning strategy for the game. Okay?
0:04:05.230,0:04:10.299
The statement is true if the prover has a
winning strategy for the
0:04:10.299,0:04:14.090
game and that means the prover has a way
of playing the game such that
0:04:14.090,0:04:17.320
whatever the skeptic does the prover is going
to win the game. The
0:04:17.320,0:04:20.789
statement is considered false if the skeptic
has a winning strategy
0:04:20.789,0:04:23.370
for the game which means the skeptic has a
way of playing so that
0:04:23.370,0:04:25.729
whatever the prover does the skeptic can win
the game.
0:04:25.729,0:04:27.599
Or if the game doesn't make sense at all
...
0:04:27.599,0:04:29.460
maybe the function is not defined on
0:04:29.460,0:04:31.050
the immediate left and right of c.
0:04:31.050,0:04:32.370
If the function isn't defined then we
0:04:32.370,0:04:34.160
cannot even make sense of the statement.
0:04:34.160,0:04:36.990
Either way -- the skeptic has a winning strategy
0:04:36.990,0:04:37.770
or the game doesn't make sense --
0:04:41.770,0:04:43.470
then the statement is false.
0:04:43.470,0:04:47.660
If the prover has a winning strategy
the statement is true.
0:04:47.660,0:04:54.660
With this background in mind let's look
at some common misconceptions.
0:04:56.540,0:05:03.540
Okay. Let's say we are trying to prove that
the limit as x approaches
0:05:27.620,0:05:31.530
2 of x^2 is 4, so is that statement correct?
The statement we're
0:05:31.530,0:05:32.060
trying to prove?
0:05:32.060,0:05:32.680
KM: Yes.
0:05:32.680,0:05:35.960
Vipul: That's correct. Because in fact x^2
is a continuous function
0:05:35.960,0:05:40.160
and the limit of a continuous function at
the point is just the
0:05:40.160,0:05:43.030
value at the point and 2^2 is 4. But we're
going to now try to prove
0:05:43.030,0:05:48.530
this formally using the epsilon-delta definition
of limit, okay? Now
0:05:48.530,0:05:51.229
in terms of the epsilon-delta definition or
rather in terms of this
0:05:51.229,0:05:55.160
game setup, what we need to do is we need
to describe a winning
0:05:55.160,0:06:01.460
strategy for the prover. Okay? We need to
describe delta in terms of
0:06:01.460,0:06:05.240
epsilon. The prover essentially ... the only
move the prover makes is
0:06:05.240,0:06:09.130
this choice of delta. Right? The skeptic picked
epsilon, the prover
0:06:09.130,0:06:12.810
picked delta then the skeptic picks x and
then they judge who won. The
0:06:12.810,0:06:15.810
only choice the prover makes is the choice
of delta, right?
0:06:15.810,0:06:16.979
KM: Exactly.
0:06:16.979,0:06:20.080
Vipul: The prover has to specify delta in terms
of epsilon.
0:06:20.080,0:06:24.819
So, here is my strategy. My strategy is I'm
going to choose delta as,
0:06:24.819,0:06:29.509
I as a prover is going to choose delta as
epsilon over the absolute
0:06:29.509,0:06:33.690
value of x plus 2 [|x + 2|]. Okay?
0:06:33.690,0:06:36.880
Now, what I want to show that this strategy
works. So, what I'm claiming
0:06:36.880,0:06:39.840
is that if ... so let me just finish this
and then you can tell me where
0:06:39.840,0:06:43.419
I went wrong here, okay? I'm claiming that
this strategy works which
0:06:43.419,0:06:47.130
means I'm claiming that if the skeptic now
picks any x which is within
0:06:47.130,0:06:54.130
delta distance of 2; the target point,
0:06:56.710,0:07:01.490
then the function value is within epsilon
distance of 4, the claimed
0:07:01.490,0:07:04.080
limit. That's what I want to show.
0:07:04.080,0:07:08.300
Now is that true? Well, here's how I do
it. I say, I start by
0:07:08.300,0:07:13.539
taking this expression, I factor it as
|x - 2||x + 2|. The absolute
0:07:13.539,0:07:16.810
value of product is the product of the absolute
values so this can be
0:07:16.810,0:07:21.599
split like that. Now I say, well, we know
that |x - 2| is less than
0:07:21.599,0:07:24.979
delta and this is a positive thing. So we
can write this as less than delta
0:07:24.979,0:07:31.979
times absolute value x plus 2. Right? And
this delta is epsilon over
0:07:35.599,0:07:37.620
|x + 2| and we get epsilon.
0:07:37.620,0:07:40.460
So, this thing equals something, less than
something, equals
0:07:40.460,0:07:43.580
something, equals something, you have a chain
of things, there's one
0:07:43.580,0:07:47.720
step that you have less than. So overall we
get that this expression,
0:07:47.720,0:07:53.740
this thing is less than epsilon. So, we have
shown that whatever x the
0:07:53.740,0:08:00.370
skeptic would pick, the function value lies
within the epsilon
0:08:00.370,0:08:05.030
distance of the claimed limit. As long as the skeptic picks x within
0:08:05.030,0:08:09.240
delta distance of the target point.
0:08:09.240,0:08:16.240
Does this strategy work? Is this a proof?
What's wrong with this?
0:08:24.270,0:08:31.270
Do you think there's anything wrong
with the algebra I've done here?
0:08:33.510,0:08:40.510
KM: Well, we said that ...
0:08:40.910,0:08:47.910
Vipul: So, is there anything wrong in the
algebra here? This is this,
0:08:50.160,0:08:51.740
this is less than delta, delta ... So, this
part
0:08:51.740,0:08:52.089
seems fine, right?
0:08:52.089,0:08:52.339
KM: Yes.
0:08:52.330,0:08:55.640
Vipul: There's nothing wrong in the algebra
here. So, what could be
0:08:55.640,0:09:00.310
wrong? Our setup seems fine. If the x value
is within delta distance
0:09:00.310,0:09:03.350
of 2 then the function value is within epsilon
distance of 4. That's
0:09:03.350,0:09:05.360
exactly what we want to prove, right?
0:09:05.360,0:09:11.120
So, there's nothing wrong this point onward.
So, the error happened
0:09:11.120,0:09:14.440
somewhere here. What do you think
was wrong
0:09:14.440,0:09:21.160
here? In the strategy choice step? What do
you think went wrong in the
0:09:21.160,0:09:24.010
strategy choice step?
0:09:24.010,0:09:28.850
Well, okay, so in what order do they play their moves?
Skeptic will choose the epsilon,
0:09:28.850,0:09:29.760
then?
0:09:29.760,0:09:35.130
KM: Then the prover chooses delta.
0:09:35.130,0:09:36.080
Vipul: Prover chooses delta. Then?
0:09:36.080,0:09:39.529
KM: Then the skeptic has to choose the x value.
0:09:39.529,0:09:42.470
Vipul: x value. So, when the prover is deciding
the strategy, when the
0:09:42.470,0:09:45.860
prover is choosing the delta, what information
does the prover have?
0:09:45.860,0:09:48.410
KM: He just has the information on epsilon.
0:09:48.410,0:09:50.500
Vipul: Just the information on epsilon. So?
0:09:50.500,0:09:57.060
KM: So, in this case the mistake was that
because he didn't know the x value yet?
0:09:57.060,0:10:03.100
Vipul: The strategy cannot depend on x.
0:10:03.100,0:10:04.800
KM: Yeah.
0:10:04.800,0:10:09.790
Vipul: So, the prover is picking the
delta based on x but the
0:10:09.790,0:10:12.660
prover doesn't know x at this stage when
picking the delta. The delta
0:10:12.660,0:10:15.910
that the prover chooses has to be completely
a function of epsilon
0:10:15.910,0:10:19.680
alone, it cannot depend on the future moves
of the skeptic because the
0:10:19.680,0:10:23.700
prover cannot read the skeptic's mind. Okay?
And doesn't know what the
0:10:23.700,0:10:24.800
skeptic plans to do.
0:10:24.800,0:10:31.800
So that is the ... that's the proof. I call
this the ...
0:10:42.240,0:10:43.040
Can you see what I call this?
0:10:43.040,0:10:45.399
KM: The strongly telepathic prover.
0:10:45.399,0:10:51.470
Vipul: So, do you know what I meant by that?
Well, I meant the prover
0:10:51.470,0:10:58.470
is reading the skeptic's mind. All
right? It's called telepathy.
0:11:07.769,0:11:10.329
0:11:10.329,0:11:17.329
Okay, the next one.
0:11:25.589,0:11:30.230
This one says there's a function defined piecewise. Okay? It's defined
0:11:30.230,0:11:34.829
as g(x) is x when x is rational and zero when
x is irrational. So,
0:11:34.829,0:11:41.829
what would this look like? Well, pictorially, there's a line y
0:11:42.750,0:11:49.510
equals x and there's the x-axis and the
graph is just the irrational x
0:11:49.510,0:11:52.750
coordinate parts of this line and the rational
x coordinate parts of
0:11:52.750,0:11:56.350
this line. It's kind of like both these
lines but only parts of
0:11:56.350,0:11:58.529
them. Right?
0:11:58.529,0:12:02.079
Now we want to show that limit as x approaches
zero of g(x) is
0:12:02.079,0:12:06.899
zero. So just intuitively, do you think the statement
is true? As x goes
0:12:06.899,0:12:09.910
to zero, does this function go to zero?
0:12:09.910,0:12:10.610
KM: Yes.
0:12:10.610,0:12:17.610
Vipul: Because both the pieces are going to
zero. That's the intuition. Okay?
0:12:20.610,0:12:24.089
This is the proof we have here. So the idea
is we again think about it
0:12:24.089,0:12:27.790
in terms of the game. The skeptic first picks
the epsilon, okay? Now
0:12:27.790,0:12:30.779
the prover has to choose the delta, but
there are really two cases
0:12:30.779,0:12:35.200
on x, right? x rational and x irrational.
So the prover chooses the
0:12:35.200,0:12:39.459
delta based on whether the x is rational
or irrational, so if
0:12:39.459,0:12:43.880
the x is rational then the prover just picks
delta equals epsilon, and
0:12:43.880,0:12:48.339
that's good enough for rational x, right?
Because for rational x the
0:12:48.339,0:12:51.410
slope of the line is one so picking delta
as epsilon is good enough.
0:12:51.410,0:12:55.760
For irrational x, if the skeptic's planning
to choose an irrational x
0:12:55.760,0:12:59.730
then the prover can just choose any delta
actually. Like just fix
0:12:59.730,0:13:03.880
a delta in advance. Like delta is one or
something. Because if x is
0:13:03.880,0:13:10.430
irrational then it's like a constant function
and therefore, like, for
0:13:10.430,0:13:14.970
any delta the function is trapped within epsilon
distance of the claimed
0:13:14.970,0:13:16.970
limit zero. Okay?
0:13:16.970,0:13:19.950
So the prover makes two cases based
on whether the skeptic is going
0:13:19.950,0:13:26.950
to pick a rational or an irrational x
and based on that if
0:13:27.040,0:13:30.730
it's rational this is the prover's strategy,
if it's irrational then
0:13:30.730,0:13:34.050
the prover can just pick any delta.
0:13:34.050,0:13:37.630
Can you tell me what's wrong with this proof?
0:13:37.630,0:13:44.630
KM: So, he [the prover] is still kind of
basing it on what the skeptic is going to
0:13:44.750,0:13:45.800
pick next.
0:13:45.800,0:13:49.100
Vipul: Okay. It's actually pretty much the
same problem [as the
0:13:49.100,0:13:55.449
preceding one], in a somewhat milder form.
The prover is making
0:13:55.449,0:13:59.959
cases based on what the skeptic is going to
do next, and choosing a
0:13:59.959,0:14:01.940
strategy according to that. But the prover
doesn't actually know what
0:14:01.940,0:14:05.089
the skeptic is going to do next, so the prover
should actually have a
0:14:05.089,0:14:08.970
single strategy that works in both cases.
So cases will be made to
0:14:08.970,0:14:12.209
prove that the strategy works but the prover
has to have a single
0:14:12.209,0:14:12.459
strategy.
0:14:12.449,0:14:15.370
Now in this case the correct way of doing the proof is just, the
0:14:15.370,0:14:18.779
prover can pick delta as epsilon because that
will work in both cases.
0:14:18.779,0:14:20.019
KM: Exactly.
0:14:20.019,0:14:23.320
Vipul: Yeah. But in general if you have two
different piece
0:14:23.320,0:14:26.579
definitions then the way you would do it so
you would pick delta as
0:14:26.579,0:14:30.300
the min [minimum] of the deltas that work in
the two different pieces,
0:14:30.300,0:14:32.910
because you want to make sure that
both cases are covered. But
0:14:32.910,0:14:36.730
the point is you have to do that -- take
the min use that rather than
0:14:36.730,0:14:39.730
just say, "I'm going to choose my delta
based on what the skeptic is
0:14:39.730,0:14:42.589
going to move next." Okay?
0:14:42.589,0:14:49.120
So this is a milder form of the same
misconception that that was there in
0:14:49.120,0:14:56.120
the previous example we saw.
0:15:04.620,0:15:11.620
So, this is what I call the mildly telepathic
prover, right? The
0:15:14.970,0:15:18.579
prover is still behaving telepathically
predicting the skeptic's future
0:15:18.579,0:15:23.740
moves but it's not so bad. The prover is
just making, like, doing a
0:15:23.740,0:15:25.470
coin toss type of telepathy. Whereas in the
earlier one is prover is
0:15:25.470,0:15:30.790
actually, deciding exactly what x the skeptic
would pick. But it's still
0:15:30.790,0:15:32.790
the same problem and the reason why I think
people will have this
0:15:32.790,0:15:36.329
misconception is because they don't think
about it in terms of the
0:15:36.329,0:15:38.970
sequence in which the moves are made, and
the information that each
0:15:38.970,0:15:45.970
party has at any given stage of the game.
0:15:50.889,0:15:57.889
Let's do this one.
0:16:10.930,0:16:15.259
So, this is a limit claim, right? It says
that the limit as x approaches
0:16:15.259,0:16:22.259
1 of 2x is 2, okay? How do we go about showing
this? Well, the idea is
0:16:23.699,0:16:27.990
let's play the game, right? Let's say
the skeptic picks epsilon as
0:16:27.990,0:16:34.990
0.1, okay? The prover picks delta as 0.05.
The skeptic is when picking
0:16:35.139,0:16:38.790
epsilon as 0.1, the skeptic is saying, "Please
trap the function
0:16:38.790,0:16:43.800
between 1.9 and 2.1. Okay? Find the delta
small enough so that the
0:16:43.800,0:16:48.389
function value is trapped between 1.9 and
2.1. The prover picks delta
0:16:48.389,0:16:55.389
as 0.05 which means the prover is now getting
the input value trapped
0:16:57.850,0:17:04.850
between 0.95 and 1.05. That's 1 plus minus
this thing. And now the
0:17:05.439,0:17:09.070
prover is claiming that if the x value is
within this much distance of
0:17:09.070,0:17:13.959
1 except the value equal to 1, then the function
value is within 0.1
0:17:13.959,0:17:17.630
distance of 2. So, the skeptic tries picking
x within the interval
0:17:17.630,0:17:23.049
specified by the prover, so maybe the skeptic
picks 0.97 which is
0:17:23.049,0:17:26.380
within 0.05 distance of 1.
0:17:26.380,0:17:31.570
And then they check that 2x [the function f(x)] is
1.94, that is at the distance of 0.06
0:17:31.570,0:17:38.570
from 2. So, it's within 0.1 of the claimed
limit 2. So who won the game?
0:17:38.780,0:17:42.650
If the thing is within the interval then who
wins?
0:17:42.650,0:17:43.320
KM: The prover.
0:17:43.320,0:17:46.720
Vipul: The prover wins, right? So, the prover
won the game so therefore
0:17:46.720,0:17:52.100
this limit statement is true, right? So, what's
wrong with this as a
0:17:52.100,0:17:57.370
proof that the limit statement is true? How
is this not a proof that
0:17:57.370,0:18:03.870
the limit statement is true? This what I've
written here, why is that
0:18:03.870,0:18:05.990
not a proof that the limit statement is true?
0:18:05.990,0:18:11.960
KM: Because it's only an example for the
specific choice of epsilon and x.
0:18:11.960,0:18:16.200
Vipul: Yes, exactly. So, it's like a single
play of the game, the
0:18:16.200,0:18:20.470
prover wins, but the limit statement doesn't
just say that the prover
0:18:20.470,0:18:24.380
wins the game, it says the prover has a winning
strategy. It says that
0:18:24.380,0:18:27.660
the prover can win the game regardless of
how the skeptic plays;
0:18:27.660,0:18:31.070
there's a way for the prover to do that.
This just gives one example
0:18:31.070,0:18:34.640
where the prover won the game, but it doesn't
tell us that regardless
0:18:34.640,0:18:37.280
of the epsilon the skeptic picks the prover
can pick a delta such that
0:18:37.280,0:18:41.090
regardless of the x the skeptic picks, the
function is within the
0:18:41.090,0:18:45.530
thing. So that's the issue here. Okay?
0:18:45.530,0:18:51.160
Now you notice -- I'm sure you've noticed
this but the way the game and the
0:18:51.160,0:18:58.160
limit definition. The way the limit definition
goes, you see that all
0:18:59.870,0:19:04.260
the moves of the skeptic we write "for every"
"for all." Right? And
0:19:04.260,0:19:07.390
for all the moves of the prover we write "there
exists." Why do we do
0:19:07.390,0:19:11.140
that? Because we are trying to get a winning
strategy for the prover,
0:19:11.140,0:19:14.309
so the prover controls his own moves. Okay?
0:19:14.309,0:19:15.250
KM: Exactly.
0:19:15.250,0:19:18.630
Vipul: So, therefore wherever it's a prover
move it will be a there
0:19:18.630,0:19:22.240
exists. Where there is a skeptic's move
the prover has to be prepared
0:19:22.240,0:19:29.240
for anything the skeptic does. All those moves
are "for every."
0:19:30.559,0:19:33.850
One last one. By the way, this one was called,
"You say you want a
0:19:33.850,0:19:36.870
replay?" Which is basically they're just
saying that just one play is
0:19:36.870,0:19:40.890
not good enough. If the statement is actually
true, the prover should
0:19:40.890,0:19:45.370
be willing to accept it if the skeptic wants a
replay and say they want to
0:19:45.370,0:19:47.679
play it again, the prover should say "sure"
and "I'm going to win
0:19:47.679,0:19:53.320
again." That's what it would mean for
the limit statement to be true.
0:19:53.320,0:20:00.320
One last one. Just kind of pretty similar
to the one we just saw. But with
0:20:16.690,0:20:23.690
a little twist.
0:20:39.020,0:20:46.020
Okay, this one, let's see. We are saying
that the limit as x
0:20:50.450,0:20:56.900
approaches zero of sin(1/x) is zero, right?
Let's see how we prove
0:20:56.900,0:21:01.409
this. If the statement true ... well, do you
think the statement is
0:21:01.409,0:21:08.409
true? As x approach to zero, is sin 1 over
x approaching zero? So
0:21:13.980,0:21:20.980
here's the picture of sin(1/x). y-axis.
It's an oscillatory function
0:21:22.010,0:21:27.870
and it has this kind of picture. Does it doesn't
go to zero as x
0:21:27.870,0:21:29.270
approaches zero?
0:21:29.270,0:21:30.669
KM: No.
0:21:30.669,0:21:35.539
Vipul: No. So, you said that this statement
is false, but I'm going to
0:21:35.539,0:21:38.700
try to show it's true. Here's how I do
that. Let's say the skeptic
0:21:38.700,0:21:44.510
picks epsilon as two, okay? And then the prover
... so, the epsilon is
0:21:44.510,0:21:48.520
two so that's the interval of width two
about the game limit zero. The
0:21:48.520,0:21:55.150
prover picks delta as 1/pi. Whatever x the
skeptic picks, okay?
0:21:55.150,0:22:02.150
Regardless of the x that the
skeptic picks, the function is trapped
within epsilon of the game limit. Is that
0:22:10.340,0:22:16.900
true? Yes, because sin
(1/x) is between minus 1 and 1, right? Therefore
0:22:16.900,0:22:20.100
since the skeptic
picked an epsilon of 2, the function value
0:22:20.100,0:22:24.030
is completely trapped in
the interval from -1 to 1, so therefore the
0:22:24.030,0:22:27.919
prover managed to trap it
within distance of 2 of the claimed limit zero.
0:22:27.919,0:22:30.970
Okay? Regardless of what
the skeptic does, right? It's not just saying
0:22:30.970,0:22:34.370
that the prover won the
game once, it's saying whatever x the skeptic
0:22:34.370,0:22:40.740
picks the prover can
still win the game. Right? Regardless if the
0:22:40.740,0:22:43.780
x the skeptic picks, the
prover picked a delta such that the function
0:22:43.780,0:22:48.100
is trapped. It's
completely trapped, okay? It's not an issue
0:22:48.100,0:22:51.130
of whether the skeptic
picked a stupid x. Do you think that this
0:22:51.130,0:22:52.130
proves the statement?
0:22:52.130,0:22:59.130
KM: No, I mean in this case it still depended
on the epsilon that the
0:23:01.030,0:23:01.820
skeptic chose.
0:23:01.820,0:23:04.980
Vipul: It's still dependent on the epsilon
that the skeptic chose? So,
0:23:04.980,0:23:05.679
yes, that's exactly the problem.
0:23:05.679,0:23:09.370
So, we proved that the statement -- we prove
that from this part onward
0:23:09.370,0:23:12.500
but it still, we didn't prove it for all
epsilon, we only prove for
0:23:12.500,0:23:16.309
epsilon is 2, and 2 is a very big number,
right? Because the
0:23:16.309,0:23:19.970
oscillation is all happening between minus
1 and 1, and if in fact the
0:23:19.970,0:23:26.970
skeptic had pick epsilon as 1 or something
smaller than 1 then the two
0:23:27.030,0:23:32.169
epsilon strip width would not cover the entire
-1, +1
0:23:32.169,0:23:35.490
interval, and then whatever the prover did
the skeptic could actually
0:23:35.490,0:23:39.530
pick an x and show that it's not trapped.
So, in fact the reason why
0:23:39.530,0:23:43.110
the prover could win the game from this point
onward is that the
0:23:43.110,0:23:45.900
skeptic made a stupid choice of epsilon.
Okay?
0:23:45.900,0:23:52.289
In all these situation, all these misconceptions,
the main problem is,
0:23:52.289,0:23:58.919
that we're not ... keeping in mind the order
which the moves I made
0:23:58.919,0:24:04.179
and how much information each claim has at
the stage where that move
0:24:04.179,0:24:04.789
is being made.
Strongly telepathic prover
Spot the error in this:
Consider the limit problem  . The
. The  proof corresponding to this problem would involve a game between a prover and a skeptic. To show that the limit statement is true, it suffices to exhibit a winning strategy for the prover for the game. The strategy is as follows. Pick
proof corresponding to this problem would involve a game between a prover and a skeptic. To show that the limit statement is true, it suffices to exhibit a winning strategy for the prover for the game. The strategy is as follows. Pick  . Let's prove that this works.
. Let's prove that this works.
Specific claim: For any skeptic-picked  , if the prover picks
, if the prover picks  such that
such that  , then regardless of the
, then regardless of the  that the skeptic picks with
that the skeptic picks with  , we have
, we have  .
.
Proof of claim: We have:

The error is as follows: [SHOW MORE]
Recall the sequence of moves made in the game. First, the skeptic picks

. Then, the prover picks

.
Then, the skeptic picks a test value of

to challenge the prover's claim of the function being trapped. In particular, this means that at the stage that the prover picks the value of

, the prover is
unaware of the value of

that the skeptic plans to pick. Hence, the prover's strategy for choosing

cannot use

. Rather, the prover must have a strategy for

purely in terms of

, which is the only piece of information known to the prover at that stage in the game.
This also explains why we called this error the strongly telepathic prover, i.e., it involved the prover reading the skeptic's mind about future planned moves, which is impermissible.
Although this strategy is wrong, it can be fixed to get a correct strategy, i.e., this is the right way to
start thinking about how this type of problem could be attacked. What the prover needs to do is pick a choice of

that works for all

that the skeptic can pick in the constrained interval. The algebra done here provides some guidelines on how the prover can make such a choice, but another idea, namely, the idea of a
cut-off value, is needed to complete the strategy.
Mildly telepathic prover
Spot the error in this:
Consider the limit problem:

We want to show that 
For this game, we need to exhibit a winning strategy for the prover. The winning strategy is as follows. The skeptic first chooses  . The prover now makes two cases. If the skeptic is planning to pick a rational value of
. The prover now makes two cases. If the skeptic is planning to pick a rational value of  , then the prover chooses the strategy
, then the prover chooses the strategy  . If the skeptic is planning to choose an irrational value of
. If the skeptic is planning to choose an irrational value of  , then the prover can pick any
, then the prover can pick any  .
.
Clearly, the prover's strategy works in both cases, so we have a winning strategy.
Th error is as follows: [SHOW MORE]
Recall the sequence of moves made in the game. First, the skeptic picks

. Then, the prover picks

.
Then, the skeptic picks a test value of

to challenge the prover's claim of the function being trapped. In particular, this means that at the stage that the prover picks the value of

, the prover is
unaware of the value of

that the skeptic plans to pick. Hence, the prover's strategy for choosing

cannot rely on specifics about what

the skeptic plans to choose.
This error is similar to the preceding error. Both involve impermissible telepathy on the prover's part in reading the skeptic's mind. The strongly telepathic prover error is more severe in the sense that it involves the prover reading the exact value of  that the skeptic plans to play, whereas the mildly telepathic prover error only involves the prover guessing the type of value (rational or irrational) that the skeptic plans to play.
that the skeptic plans to play, whereas the mildly telepathic prover error only involves the prover guessing the type of value (rational or irrational) that the skeptic plans to play.
The fix for the mildly telepathic prover error is that the prover chooses a
combined strategy that
simultaneously works for both eventualities. In this situation, the strategy

works for both situations (rational and irrational

). In general, for a function with two piece definitions for rational and irrational points in the domain, we need to take the
min of the

-strategies that work for the definitions individually. A similar approach works for different definitions on the left and right.
You say you want a replay?
Spot the error in this:
Consider the limit problem  . Let's think of this in terms of an
. Let's think of this in terms of an  game. The skeptic begins by picking
game. The skeptic begins by picking  . The prover chooses
. The prover chooses  . The skeptic now chooses
. The skeptic now chooses  . This value of
. This value of  is within the
is within the  -distance of
-distance of  . It's now checked that
. It's now checked that  is within
is within  -distance of the claimed limit
-distance of the claimed limit  . The prover has thus won the game, and we have established the truth of the limit statement.
. The prover has thus won the game, and we have established the truth of the limit statement.
The error is as follows: [SHOW MORE]
This involves
only one play of the

limit game. The prover did win this play of the game. However, for us to declare the limit statement to be true, we need to establish that the prover has a
winning strategy for the game, which means we need to demonstrate how the prover would pick a

in terms of each choice of

(preferably by specifying

explicitly as a function of

) and then show that the strategy works for all

within

-distance of the point on the domain side.
It so happens that in this case, the limit statement is true and the prover did play the game according to one possible winning strategy:

. However, since we weren't actually told the winning strategy, let alone given an explanation of why it works, what we're given fails as a proof.
Playing to lose
Spot the error in this:
Here's an easy proof that  . We need to show that the prover has a winning strategy for the game. Let's say the skeptic starts out by picking
. We need to show that the prover has a winning strategy for the game. Let's say the skeptic starts out by picking  . The prover then picks
. The prover then picks  . It can now easily be verified that for
. It can now easily be verified that for  ,
,  , because the
, because the  function is trapped within
function is trapped within ![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01) . Thus, the prover has succeeded in trapping the function within the $\varepsilon$-interval specified by the skeptic, and hence won the game. The limit statement is therefore true.
. Thus, the prover has succeeded in trapping the function within the $\varepsilon$-interval specified by the skeptic, and hence won the game. The limit statement is therefore true.
The error is as follows: [SHOW MORE]
This involves
only one choice of

. The proof does show that with the choice

, the prover wins the game. However, in order to show that the limit statement is true, one would need to demonstrate that the prover wins the game for
every possible choice of

. In particular, from the skeptic's viewpoint,
smaller is smarter, so the prover needs to have a strategy to win the game for arbitrarily small

.
In fact, the limit statement is false, and for any choice of

, the prover
cannot win the game, because the range of the function on the immediate left and immediate right of zero is
![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)
.
Conceptual definition and various cases
Formulation of conceptual definition
Below is the conceptual definition of limit. Suppose  is a function defined in a neighborhood of the point
is a function defined in a neighborhood of the point  , except possibly at the point
, except possibly at the point  itself. We say that:
itself. We say that:

if:
- For every choice of neighborhood of
 (where the term neighborhood is suitably defined)
(where the term neighborhood is suitably defined)
- there exists a choice of neighborhood of
 (where the term neighborhood is suitably defined) such that
(where the term neighborhood is suitably defined) such that
- for all
 that are in the chosen neighborhood of
that are in the chosen neighborhood of 
 is in the chosen neighborhood of
is in the chosen neighborhood of  .
.
{{#widget:YouTube|id=bE_aKfmUHN8}}
Full timed transcript: [SHOW MORE]
0:00:15.570,0:00:19.570
Vipul: Ok, so in this talk I'm going to
do the conceptual definition
0:00:19.570,0:00:26.320
of limit, which is important for a number
of reasons. The main reason
0:00:26.320,0:00:31.349
is it allows you to construct definitions
of limit, not just for this
0:00:31.349,0:00:34.430
one variable, function of one variable, two
sided limit which you have
0:00:34.430,0:00:38.930
hopefully seen before you saw this video.
Also for a number of other
0:00:38.930,0:00:43.210
limit cases which will include limits to infinity,
functions of two
0:00:43.210,0:00:47.789
variables, etc. So this is a general blueprint
for thinking about
0:00:47.789,0:00:54.789
limits. So let me put this definition here
in front for this. As I am
0:00:54.890,0:00:59.289
going, I will write things in more general.
So the starting thing is...
0:00:59.289,0:01:03.899
first of all f should be defined around the
point c, need not be
0:01:03.899,0:01:08.810
defined at c, but should be defined everywhere
around c. I won't write
0:01:08.810,0:01:11.750
that down, I don't want to complicate things
too much. So we start
0:01:11.750,0:01:18.750
with saying for every epsilon greater than
zero. Why are we picking
0:01:19.920,0:01:21.689
this epsilon greater than zero?
0:01:21.689,0:01:22.790
Rui: Why?
0:01:22.790,0:01:26.070
Vipul: What is the goal of this epsilon? Where
will it finally appear?
0:01:26.070,0:01:28.520
It will finally appear here. Is this captured?
0:01:28.520,0:01:29.520
Rui: Yes.
0:01:29.520,0:01:32.920
Vipul: Which means what we actually are picking
when we...if you've
0:01:32.920,0:01:37.720
seen the limit as a game video or you know
how to make a limit as a
0:01:37.720,0:01:41.700
game. This first thing has been chosen by
the skeptic, right, and the
0:01:41.700,0:01:45.840
skeptic is trying to challenge the prover
into trapping f(x) within L - epsilon to
0:01:45.840,0:01:50.210
L + epsilon. Even if you haven't
seen that [the game], the main focus of
0:01:50.210,0:01:55.570
picking epsilon is to pick this interval surrounding
L. So instead of
0:01:55.570,0:02:02.570
saying, for every epsilon greater than zero,
let's say for every
0:02:04.259,0:02:11.259
choice of neighborhood of L. So what I mean
by that, I have not
0:02:19.650,0:02:23.760
clearly defined it so this is a definition
which is not really a
0:02:23.760,0:02:28.139
definition, sort of the blueprint for definitions.
It is what you fill
0:02:28.139,0:02:31.570
in the details [of] and get a correct definition.
So by neighborhood,
0:02:31.570,0:02:36.180
I mean, in this case, I would mean something
like (L - epsilon, L +
0:02:36.180,0:02:43.180
epsilon). It is an open interval surrounding
L. Ok, this one. The
0:02:44.590,0:02:47.160
conceptual definition starts for every choice
of neighborhood of
0:02:47.160,0:02:54.160
L. The domain neighborhood, I haven't really
defined, but that is the
0:02:58.359,0:03:05.359
point, it is the general conceptual definition.
There exists...what
0:03:09.810,0:03:11.530
should come next? [ANSWER!]
0:03:11.530,0:03:16.530
Rui: A delta?
Vipul: That is what the concrete definition
0:03:16.530,0:03:18.530
says, but what would the
conceptual thing say?
0:03:18.530,0:03:21.680
Rui: A neighborhood.
Vipul: Of what? [ANSWER!]
0:03:21.680,0:03:28.680
Rui: Of c.
Vipul: Of c, of the domain. The goal of picking
0:03:34.639,0:03:37.970
delta is to find a
neighborhood of c. Points to the immediate
0:03:37.970,0:03:44.919
left and immediate
right of c. There exists a choice of neighborhood
0:03:44.919,0:03:51.919
of c such that, by
the way I sometimes abbreviate, such that,
0:03:59.850,0:04:06.109
as s.t., okay, don't get
confused by that. Okay, what next? Let's
0:04:06.109,0:04:12.309
bring out the thing. The next
thing is for all x with |x - c| less than
0:04:12.309,0:04:19.309
... all x in the neighborhood
except the point c itself. So what should
0:04:20.040,0:04:27.040
come here? For all x in the
neighborhood of c, I put x not equal to c.
0:04:36.570,0:04:37.160
Is that clear?
0:04:37.160,0:04:37.520
Rui: Yes.
0:04:37.520,0:04:44.520
Vipul: x not equal to c in the neighborhood
chosen for c. The reason
0:04:49.310,0:04:53.360
we're excluding the point c that we take the
limit at the point and we
0:04:53.360,0:04:55.770
just care about stuff around, we don't care
about what is happening at
0:04:55.770,0:05:02.770
the point. For c...this chosen neighborhood...I
am writing the black
0:05:09.880,0:05:14.440
for choices that the skeptic makes and the
red for the choices the
0:05:14.440,0:05:16.490
prover makes, actually that's reverse of what
I did in the other
0:05:16.490,0:05:21.320
video, but that's ok. They can change colors.
If you have seen that
0:05:21.320,0:05:24.710
limit game thing, this color pattern just
[means] ... the black
0:05:24.710,0:05:28.400
matches with the skeptic choices and the red
matches what the prover
0:05:28.400,0:05:32.710
chooses. If you haven't seen that, it is
not an issue. Just imagine
0:05:32.710,0:05:35.820
it's a single color.
0:05:35.820,0:05:40.820
What happens next? What do we need to check
in order to say this limit
0:05:40.820,0:05:42.950
is L? So f(x) should be where?
0:05:42.950,0:05:44.980
Rui: In the neighborhood of L.
0:05:44.980,0:05:48.060
Vipul: Yeah. In the concrete definition we
said f(x) minus L is less
0:05:48.060,0:05:51.440
than epsilon. Right, but that is just stating
that f(x) is in the
0:05:51.440,0:05:58.440
chosen neighborhood. So f(x) is in the chosen
neighborhood of...Now
0:06:08.470,0:06:15.470
that we have this blueprint for the definition.
This is a blueprint
0:06:25.660,0:06:32.660
for the definition. We'll write it in blue.
What I mean is, now if I
0:06:34.930,0:06:40.700
ask you to define a limit, in a slightly different
context; you just
0:06:40.700,0:06:46.280
have to figure out in order to make this rigorous
definition. What
0:06:46.280,0:06:49.240
word do you need to understand the meaning
of? [ANSWER!]
0:06:49.240,0:06:53.780
Rui: Neighborhood.
Vipul: Neighborhood, right. That's the magic
0:06:53.780,0:06:59.810
word behind which I am
hiding the details. If you can understand
0:06:59.810,0:07:06.280
what I mean by neighborhood
then you can turn this into a concrete definition.
Functions of one variable case
The following definitions of neighborhood are good enough to define limits.
- For points in the interior of the domain, for functions of one variable: We can take an open interval centered at the point. For a point
 , such an open interval is of the form
, such an open interval is of the form  . Note that if we exclude the point
. Note that if we exclude the point  itself, we get
itself, we get  .
.
- For the point
 , for functions of one variable: We take intervals of the form
, for functions of one variable: We take intervals of the form  , where
, where  .
.
- For the point
 , for functions of one variable: We can take interval of the form
, for functions of one variable: We can take interval of the form  , where
, where  .
.
We can now list the nine cases of limits, combining finite and infinite possibilities:
| Case |
Definition
|
 |
For every  , there exists , there exists  such that for all such that for all  satisfying satisfying  (i.e., (i.e.,  ), we have ), we have  (i.e., (i.e.,  ). ).
|
 |
For every  , there exists , there exists  such that for all such that for all  satisfying satisfying  (i.e., (i.e.,  ), we have ), we have  (i.e., (i.e.,  ). ).
|
 |
For every  , there exists , there exists  such that for all such that for all  satisfying satisfying  (i.e., (i.e.,  ), we have ), we have  (i.e., (i.e.,  ). ).
|
 |
For every  , there exists , there exists  such that for all such that for all  satisfying satisfying  (i.e., (i.e.,  ), we have ), we have  (i.e., (i.e.,  ). ).
|
 |
For every  , there exists , there exists  such that for all such that for all  satisfying satisfying  (i.e., (i.e.,  ), we have ), we have  (i.e., (i.e.,  ). ).
|
 |
For every  , there exists , there exists  such that for all such that for all  satisfying satisfying  (i.e., (i.e.,  ), we have ), we have  (i.e., (i.e.,  ). ).
|
 |
For every  , there exists , there exists  such that for all such that for all  satisfying satisfying  (i.e., (i.e.,  ), we have ), we have  (i.e., (i.e.,  ). ).
|
 |
For every  , there exists , there exists  such that for all such that for all  satisfying satisfying  (i.e., (i.e.,  ), we have ), we have  (i.e., (i.e.,  ). ).
|
 |
For every  , there exists , there exists  such that for all such that for all  satisfying satisfying  (i.e., (i.e.,  ), we have ), we have  (i.e., (i.e.,  ). ).
|
{{#widget:YouTube|id=EOQby7b-WrA}}
Limit of sequence versus real-sense limit
Recall that the limit of a real-valued function to infinity is defined as follows:
 means that:
means that:
- For every

- there exists
 (we're thinking of the neighborhood
(we're thinking of the neighborhood  ) such that
) such that
- for all
 (i.e.
(i.e.  )
)
- we have
 (i.e.,
(i.e.,  ).
).
Suppose now instead that  is a function restricted to the natural numbers. We can think of
is a function restricted to the natural numbers. We can think of  as a sequence, namely the sequence
as a sequence, namely the sequence  . In that case:
. In that case:
 (in words, the sequence converges to
(in words, the sequence converges to  ) means that:
) means that:
- For every

- there exists
 such that
such that
- for all
 satisfying
satisfying  ,
,
- we have
 (i.e.,
(i.e.,  ).
).
The definitions differ both in their second and third line. However, the difference in the second line (the use of a real number versus a natural number to specify the threshold for the trapping interval) is not important, i.e., we could swap these lines between the definitions without changing the sense of either definition. The key difference between the definitions lies in their third lines. In the real-sense limit definition case, we require trapping of the function value close to the claimed limit for all sufficiently large reals whereas the sequence limit definition requires trapping only for all sufficiently large natural numbers.
To understand this distinction, consider the following: if  is defined on reals, and it has a real-sense limit, i.e.,
is defined on reals, and it has a real-sense limit, i.e.,  for some
for some  , then it must also be true that
, then it must also be true that  . However, it is possible for
. However, it is possible for  to have a sequence limit but not have a real-sense limit. For instance, the function
to have a sequence limit but not have a real-sense limit. For instance, the function  has
has  undefined but
undefined but  is zero, because
is zero, because  takes the value 0 at all integers.
takes the value 0 at all integers.
{{#widget:YouTube|id=P9APtpIE4y8}}
Full timed transcript: [SHOW MORE]
0:00:15.530,0:00:22.530
Vipul: Okay. So this talk is going to be about
limit at infinity for functions on real numbers
0:00:24.300,0:00:28.980
and the concept of limits of sequences, how
these definitions are essentially almost the
0:00:28.980,0:00:34.790
same thing and how they differ.
0:00:34.790,0:00:41.790
Okay. So let's begin by reviewing the definition
of the limit as x approaches infinity of f(x).
0:00:42.360,0:00:47.390
Or rather what it means for that limit to
be a number L. Well, what it means is that
0:00:47.390,0:00:52.699
for every epsilon greater than zero, so we
first say for every neighborhood of L, small
0:00:52.699,0:00:59.429
neighborhood of L, given by radius epsilon
there exists a neighborhood of infinity which
0:00:59.429,0:01:03.010
is specified by choosing some a such that
that is
0:01:03.010,0:01:08.670
the interval (a,infinity) ...
0:01:08.670,0:01:15.220
... such that for all x in the interval from
a to infinity. That is for all x within the
0:01:15.220,0:01:20.430
chosen neighborhood of infinity, the f(x)
value is within the chosen neighborhood of
0:01:20.430,0:01:23.390
L. Okay?
0:01:23.390,0:01:28.049
If you want to think about it in terms of
the game between the prover and the skeptic,
0:01:28.049,0:01:34.560
the prover is claiming that the limit as x
approaches infinity of f(x) is L. The skeptic
0:01:34.560,0:01:38.930
begins by picking a neighborhood of L which
is parameterized by its radius epsilon. The
0:01:38.930,0:01:41.619
prover picks the
neighborhood of infinity which is parameterized
0:01:41.619,0:01:48.350
by its lower end a. Then the skeptic picks
a value x between a and infinity. Then they
0:01:48.350,0:01:51.990
check whether absolute value f(x) minus L
[symbolically: |f(x) - L|] is less than epsilon.
0:01:51.990,0:01:56.090
That is they check whether f(x) is in the
chosen neighborhood of L (the neighborhood
0:01:56.090,0:02:00.640
chosen by the skeptic). If it is,
then the prover wins. The prover has managed
0:02:00.640,0:02:05.810
to trap the function: for x large enough,
the prover has managed to trap the function
0:02:05.810,0:02:12.810
within epsilon distance of L. If not, then
the skeptic wins. The statement is true if
0:02:13.610,0:02:18.680
the prover has a winning the strategy for
the game.
0:02:18.680,0:02:21.730
Now, there is a similar definition which one
has for sequences. So, what's a sequence?
0:02:21.730,0:02:26.349
Well, it's just a function from the natural
numbers. And, here, we're talking of sequences
0:02:26.349,0:02:31.610
of real numbers. So, it's a function from
the naturals to the reals and we use the same
0:02:31.610,0:02:37.400
letter f for a good reason. Usually we write
sequences with subscripts, a_n type of thing.
0:02:37.400,0:02:42.409
But I'm using it as a function just to highlight
the similarities. So, limit as n approaches
0:02:42.409,0:02:47.519
infinity, n restricted to the natural numbers
... Usually if it's clear we're talking of
0:02:47.519,0:02:52.830
a sequence, we can remove this part [pointing
to the n in N constraint specification] just
0:02:52.830,0:02:54.980
say limit n approaches infinity f(n),
but since we want to be really clear here,
0:02:54.980,0:02:57.220
I have put this line. Okay?
0:02:57.220,0:03:02.709
So, this limit equals L means "for every epsilon
greater than 0 ..." So, it starts in the same
0:03:02.709,0:03:09.170
way. The skeptic picks a neighborhood of L.
Then the next line is a little different but
0:03:09.170,0:03:16.170
that's not really the crucial part. The skeptic
is choosing epsilon. The prover picks n_0,
0:03:18.799,0:03:22.830
a natural number. Now, here the prover is
picking a real number. Here the prover is
0:03:22.830,0:03:26.700
picking a natural number. That's not really
the big issue. You could in fact change this
0:03:26.700,0:03:33.659
line to match. You could interchange these
lines. It wouldn't affect either definition.
0:03:33.659,0:03:40.599
The next line is the really important one
which is different. In here [pointing to real-sense
0:03:40.599,0:03:47.430
limit], the condition has to be valid for
all x, for all real numbers x which are bigger
0:03:47.430,0:03:51.900
than the threshold which the prover has chosen.
Here on the other hand [pointing to the sequence
0:03:51.900,0:03:56.970
limit] the condition has to be valid for all
natural numbers which are bigger than the
0:03:56.970,0:04:00.659
threshold the prover has chosen. By the way,
some of you may have seen the definition with
0:04:00.659,0:04:07.659
an equality sign here. It doesn't make a difference
to the definition. It does affect what n_0
0:04:09.010,0:04:12.019
you can choose, it will go up or down by one,
but that's not
0:04:12.019,0:04:17.310
really a big issue. The big issue, the big
difference between these two definitions is
0:04:17.310,0:04:23.050
that in this definition you are insisting
that the condition here is valid for all real
0:04:23.050,0:04:30.050
x. So, you are insisting or rather the game
is forcing the prover to figure out how to
0:04:31.650,0:04:36.940
trap the function values for all real x. Whereas
here, the game is only requiring the prover
0:04:36.940,0:04:39.639
to trap the function values for all large
enough
0:04:39.639,0:04:42.880
natural numbers. So, here [real-sense limit]
it's all large enough real numbers. Here [sequence
0:04:42.880,0:04:49.250
limit] it's all large enough natural numbers.
Okay?
0:04:49.250,0:04:56.250
So, that's the only difference essentially.
Now, you can see from the way we have written
0:04:57.050,0:04:59.900
this that this [real-sense limit] is much
stronger. So, if you do have a function which
0:04:59.900,0:05:06.880
is defined on real so that both of these concepts
can be discussed. If it were just a sequence
0:05:06.880,0:05:10.080
and there were no function to talk about then
obviously, we can't even talk about this.
0:05:10.080,0:05:16.860
If there's a function defined on the reals
or on all large enough reals, then we can
0:05:16.860,0:05:21.470
try taking both of these. The existence of
this [pointing at the real-sense limit] and
0:05:21.470,0:05:24.580
[said "or", meant "and"] it's being equal
to L as much stronger than this [the sequence
0:05:24.580,0:05:27.250
limit] equal to L. If this is equal to L then
definitely this [the sequence limit] is equal
0:05:27.250,0:05:29.330
to L. Okay?
0:05:29.330,0:05:32.080
But maybe there are situations where this
[the sequence limit] is equal to some number
0:05:32.080,0:05:38.240
but this thing [the real-sense limit] doesn't
exist. So, I want to take one example here.
0:05:38.240,0:05:45.240
I have written down an example and we can
talk a bit about that is this. So, here is
0:05:45.509,0:05:52.509
a function. f(x) = sin(pi x). This is sin
(pi x) and the corresponding
0:05:55.630,0:06:00.530
function if you just restrict [it] to the
natural numbers is just sin (pi n). Now, what
0:06:00.530,0:06:06.759
does sin (pi n) look like for a natural number
n? In fact for any integer n? pi times
0:06:06.759,0:06:13.759
n is an integer multiple of pi. sin of integer
multiples of pi is zero. Let's make a picture
0:06:18.370,0:06:25.370
of sin ...
0:06:27.289,0:06:33.360
It's oscillating. Right? Integer multiples
of pi are precisely the ones where it's meeting
0:06:33.360,0:06:40.330
the axis. So, in fact we are concerned about
the positive one because we are talking of
0:06:40.330,0:06:45.840
the sequence (natural number [inputs]). Okay?
And so, if you are looking at this sequence,
0:06:45.840,0:06:51.090
all the terms here are zero. So, the limit
is also zero. So, this limit [the sequence
0:06:51.090,0:06:53.030
limit] is zero.
0:06:53.030,0:07:00.030
Okay. What about this limit? Well, we have
the picture again. Is it going anywhere? No.
0:07:05.349,0:07:07.650
It's oscillating between minus one and one
[symbolically: oscillating in [-1,1]]. It's
0:07:07.650,0:07:11.669
not settling down to any number. It's not...
You cannot trap it near any particular number
0:07:11.669,0:07:17.280
because it's all over the map between minus
one and one. For the same reason that sin(1/x)
0:07:17.280,0:07:22.840
doesn't approach anything as x approaches
zero, the same reason sin x or sin(pi x) doesn't
0:07:22.840,0:07:29.840
approach anything as x approaches infinity.
So, the limit for the real thing, this does
0:07:31.099,0:07:37.539
not exist. So, this gives an example where
the real thing [the real-sense limit] doesn't
0:07:37.539,0:07:44.539
exist and the sequence thing [sequence limit]
does exist and so here is the overall summary.
0:07:44.690,0:07:46.979
If the real sense limit,
that is this one [pointing to definition of
0:07:46.979,0:07:51.039
real sense limit] exists, [then] the sequence
limit also exists and they're both equal.
0:07:51.039,0:07:54.419
On the other hand, you can have a situation
with the real sense limit, the limit for the
0:07:54.419,0:08:00.819
function of reals doesn't exist but the sequence
limit still exists like this set up. Right?
0:08:00.819,0:08:05.569
Now, there is a little caveat that I want
to add. If the real sense limit doesn't exist
0:08:05.569,0:08:11.069
as a finite number but it's say plus infinity
then the sequence limit also has to be plus
0:08:11.069,0:08:16.150
infinity. If the real sense limit is minus
infinity, then the sequence limit also has
0:08:16.150,0:08:20.330
to be minus infinity. So, this type of situation,
where the real sense limit doesn't exist but
0:08:20.330,0:08:26.840
the sequence exists, well, will happen in
kind of oscillatory type of situations. Where
0:08:26.840,0:08:31.409
the real sense you have an oscillating thing
and in the sequence thing on the other hand
0:08:31.409,0:08:36.330
you somehow manage to pick a bunch of points
where that oscillation doesn't create a problem.
0:08:36.330,0:08:36.789
Okay?
0:08:36.789,0:08:43.630
Now, why is this important? Well, it's important
because in a lot of cases when you have to
0:08:43.630,0:08:50.630
calculate limits of sequences, you just calculate
them by doing, essentially, just calculating
0:08:53.230,0:09:00.230
the limits of the function defining the sequence
as a limit of a real valued function. Okay?
0:09:00.230,0:09:03.460
So, for instance if I ask you what is limit
...
0:09:03.460,0:09:10.460
Okay. I'll ask you what is limit [as] n approaches
infinity of n^2(n + 1)/(n^3 + 1) or something
0:09:15.200,0:09:22.200
like that. Right? Some rational function.
You just do this calculation as if you were
0:09:25.430,0:09:29.720
just doing a limit of a real function, function
of real numbers, right? The answer you get
0:09:29.720,0:09:33.060
will be the correct one. If it's a finite
number it will be the same finite number.
0:09:33.060,0:09:37.850
In this case it will just be one. But any
rational function, if the answer is finite,
0:09:37.850,0:09:44.070
same answer for the sequence. If it is plus
infinity, same answer for the sequence. If
0:09:44.070,0:09:46.250
it is minus infinity, same answer as for the
sequence.
0:09:46.250,0:09:53.250
However, if the answer you get for the real-sense
limit is oscillatory type of non existence,
0:09:54.660,0:09:59.410
then that's inconclusive as far as the sequence
is concerned. You actually have to think about
0:09:59.410,0:10:05.520
the sequence case and figure out for yourself
what happens to the limit. Okay? If might
0:10:05.520,0:10:07.230
in
fact be the case that the sequence limit actually
0:10:07.230,0:10:11.380
does exist even though the real sense [limit]
is oscillatory. Okay.
Real-valued functions of multiple variables case
We consider the multiple input variables as a vector input variable, as the definition is easier to frame from this perspective.
The correct notion of neighborhood is as follows: for a point  , we define the neighborhood parametrized by a positive real number
, we define the neighborhood parametrized by a positive real number  as the open ball of radius
as the open ball of radius  centered at
centered at  , i.e., the set of all points
, i.e., the set of all points  such that the distance from
such that the distance from  to
to  is less than
is less than  . This distance is the same as the norm of the difference vector
. This distance is the same as the norm of the difference vector  . The norm is sometimes denoted
. The norm is sometimes denoted  . This open ball is sometimes denoted
. This open ball is sometimes denoted  .
.
Suppose  is a real-valued (i.e., scalar) function of a vector variable
is a real-valued (i.e., scalar) function of a vector variable  . Suppose
. Suppose  is a point such that
is a point such that  is defined "around"
is defined "around"  , except possibly at
, except possibly at  . In other words, there is an open ball centered at
. In other words, there is an open ball centered at  such that
such that  is defined everywhere on that open ball, except possibly at
is defined everywhere on that open ball, except possibly at  .
.
With these preliminaries out of the way, we can define the notion of limit. We say that:

if the following holds:
- For every

- there exists
 such that
such that
- for all
 satisfying
satisfying  (i.e.,
(i.e.,  is in a ball of radius
is in a ball of radius  centered at
centered at  but not the point
but not the point  itself -- note that the
itself -- note that the  notation is for the norm, or length, of a vector)
notation is for the norm, or length, of a vector)
- we have
 . Note that
. Note that  and
and  are both scalars, so the
are both scalars, so the  here is the usual absolute value function.
here is the usual absolute value function.
{{#widget:YouTube|id=usb3jew_QVI}}




































































![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)













































































