First derivative test is inconclusive for function whose derivative has ambiguous sign around the point

Statement

Goal of statement

The goal of this statement is to identify a type of situation where the first derivative test is inconclusive.

One-sided version

Suppose $f$ is a real-valued function of one variable and $c$ is a point in the domain of $f$.

Continuity and differentiability assumption	Hypothesis on sign of derivative $f'$	Conclusion
$f$ is left continuous at $c$ and differentiable on the immediate left of $c$	$f'$ has oscillating sign on the immediate left of $c$, i.e., for any $\delta >0$, $f'(x)$ takes both positive and negative values for $x\in (c-\delta ,c)$.	$f$ may have a local maximum from the left at $c$, local minimum from the left at $c$, or neither.
$f$ is right continuous at $c$ and differentiable on the immediate right of $c$	$f'$ has oscillating sign on the immediate right of $c$, i.e., for any $\delta >0$, $f'(x)$ takes both positive and negative values for $x\in (c,c+\delta )$.	$f$ may have a local maximum from the right at $c$, local minimum from the right at $c$, or neither.

Two-sided version

Suppose $f$ is a real-valued function of one variable and $c$ is a point in the domain of $f$.

Continuity and differentiability assumption	Sign of $f'$ on immediate left	Sign of $f'$ on immediate right	Conclusion
$f$ is continuous at $c$ and differentiable on the immediate left and immediate right of $c$	oscillatory	oscillatory	$f$ may have a local maximum, local minimum, or neither
$f$ is continuous at $c$ and differentiable on the immediate left and immediate right of $c$	oscillatory	positive	$f$ has a strict local minimum from the right. Hence, overall, it cannot have a local maximum at $c$. It could have a local minimum or no local extremum.
$f$ is continuous at $c$ and differentiable on the immediate left and immediate right of $c$	oscillatory	negative	$f$ has a strict local maximum from the right. Hence, overall, it cannot have a local minimum at $c$. It could have a local maximum or no local extremum.
$f$ is continuous at $c$ and differentiable on the immediate left and immediate right of $c$	positive	oscillatory	$f$ has a strict local maximum from the left. Hence, overall, it cannot have a local minimum at $c$. It could have a local maximum or no local extremum.
$f$ is continuous at $c$ and differentiable on the immediate left and immediate right of $c$	negative	oscillatory	$f$ has a strict local minimum from the left. Hence, overall, it cannot have a local maximum at $c$. It could have a local minimum or no local extremum.

Relation with critical points

In all the two-sided cases, the point $c$ under consideration must be a critical point for the function (i.e., either $f'(c)=0$ or $f'(c)$ does not exist). Thus, we could add, to each case, the additional condition that $c$ be a critical point for the function, and this will not affect the strength of the statements.

Example

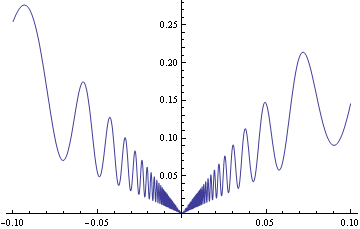
Example of two-sided local minimum despite oscillatory sign of derivative around the point

The function illustrated in the picture is:

$f(x):=\lbrace {\begin{array}{rl}|x|\left(2+\sin \left({\frac {1}{x}}\right)\right),&x\neq 0\\0,&x=0\\\end{array}}$

We note the following:

Assertion	Explanation
$f$ has a strict local and absolute minimum at 0	For $x\neq 0$, we have $f(x)>0=f(0)$. This is because $|x|>0$ and $2+\sin(1/x)\in [1,3]$, so that is also positive.
$f$ is continuous at 0	We can see this using the pinching theorem (by pinching the function between $|x|$ and $3|x|$) or more directly by noting that as $x\to 0$, $|x|\to 0$ and $2+\sin(1/x)$ is bounded between finite values 1 and 3.
$f'$ has oscillatory sign on the immediate left of 0	For $x<0$, we have $f(x)=-x(2+\sin(1/x))$. The derivative is $f'(x)=-2-\sin(1/x)+(1/x)\cos(1/x)$. The part $-2-\sin(1/x)$ is boundd, but the part $(1/x)\cos(1/x)$ oscillates between large magnitude positive and negative values as $x\to 0^{-}$. In particular, $f'$ does not have constant sign on the immediate left of 0.
$f'$ has oscillatory sign on the immediate right of 0	For $x>0$, we have $f(x)=x(2+\sin(1/x))$. The derivative is $f'(x)=2+\sin(1/x)-(1/x)\cos(1/x)$. The part $2+\sin(1/x)$ is bounded, but the part $-(1/x)\cos(1/x)$ oscillates between large magnitude positive and negative values as $x\to 0^{+}$. In particular, $f'$ does not have constant sign on the immediate right of 0.

Example of oscillatory sign of derivative where the function does not have a local extremum from either side

An example is:

$f(x):=\lbrace {\begin{array}{rl}x\sin(1/x),&x\neq 0\\0,&x=0\\\end{array}}$

Assertion	Construction
$f$ does not have a local extremum at 0 from either side	This is because $f$ takes both positive and negative values as $x\to 0^{+}$. Also, $f$ takes both positive and negative values as $x\to 0^{-}$.
$f$ is continuous at 0	We can see this using the pinching theorem or more directly by noting that as $x\to 0$, the factor $x\to 0$ and the factor $\sin(1/x)$ is bounded between finite values -1 and 1.
$f'$ has oscillatory sign to the immediate left of 0	The derivative is $f'(x)=\sin(1/x)-(1/x)\cos(1/x)$. The $\sin(1/x)$ part is bounded, but the part $-(1/x)\cos(1/x)$ oscillates between large magnitude positive and negative values as $x\to 0^{-}$. In particular, $f'$ does not have constant sign on the immediate left of 0.
$f'$ has oscillatory sign to the immediate right of 0	The derivative is $f'(x)=\sin(1/x)-(1/x)\cos(1/x)$. The $\sin(1/x)$ part is bounded, but the part $-(1/x)\cos(1/x)$ oscillates between large magnitude positive and negative values as $x\to 0^{+}$. In particular, $f'$ does not have constant sign on the immediate right of 0.

Variations that cover all cases

The above two examples can be modified to produce examples for all the cases mentioned in the statement. To convert local minimum to local maximum, multiply the whole function by $-1$. To obtain one-sided behavior, restrict the analysis to one side. Also, use piecewise combinations with functions that are nice on the other side to obtain other examples for two-sided behavior.

In all cases, we take the point $c=0$ and the value $f(0)=0$ for convenience in all examples. This allows us to easily make two-sided combinations.

One-sided requirement	Example function (definition only on appropriate side)
Oscillatory sign of derivative on left, but function has strict local maximum from left	$f(x):=\left\lbrace {\begin{array}{rl}x\left(2+\sin \left({\frac {1}{x}}\right)\right),&x<0\\0,&x=0\\\end{array}}\right.$
Oscillatory sign of derivative on left, but function has strict local minimum from left	Failed to parse (syntax error): {\displaystyle f(x) := \lbrace\begin{array}{rl} (-x)\left(2 + \sin\left(\frac{1}{x}\right)\right), & x < 0 \\ 0, & x = 0 \\\end{array} \right.}
Oscillatory sign of derivative on left, and function has neither local maximum nor local minimum from left	$f(x):=\left\lbrace {\begin{array}{rl}x\sin(1/x),&x<0\\0,&x=0\\\end{array}}\right.$
Oscillatory sign of derivative on right, but function has strict local maximum from right	$f(x):=\left\lbrace {\begin{array}{rl}(-x)\left(2+\sin \left({\frac {1}{x}}\right)\right),&x>0\\0,&x=0\\\end{array}}\right.$
Oscillatory sign of derivative on right, but function has strict local minimum from right	Failed to parse (syntax error): {\displaystyle f(x) := \lbrace\begin{array}{rl} x\left(2 + \sin\left(\frac{1}{x}\right)\right), & x > 0 \\ 0, & x = 0 \\\end{array} \right.}
Oscillatory sign of derivative on right, and function has neither local maximum nor local minimum from right	$f(x):=\left\lbrace {\begin{array}{rl}x\sin(1/x),&x>0\\0,&x=0\\\end{array}}\right.$